Современные информационные технологии Вычислительная техника и программирование
Действительный член, профессор РАЕ, Почетный доктор наук
РАЕ, Заслуженный работник науки и образования РАЕ, к. т. н. ВАК РФ, доц. ВАК
РФ Буянкин В. М.
Московский Государственный
технический университет им.
Н.Э.Баумана,Россия,
ПУТИ УВЕЛИЧЕНИЯ БЫСТРОДЕЙСТВИЯ ОБУЧЕНИЯ НЕЙРОИДЕНТИФИКАТОРОВ
Аннотация
При
нейроидентификации различных систем управления технологическими
устройствами, которые работают в
реальном масштабе времени, необходимо решать задачу выбора нейронной сети
с минимальным временем обучения. В статье предлагается эффективный метод увеличения
быстродействия работы нейроидентификаторов с
отсеканием локальных минимумов ошибки обучения. Другой, предлагаемый в статье
эффективный метод увеличения быстродействия работы нейроидентификаторов возможен
за счет динамического изменения величины шага обучения. Система управления состоит из блоков, которые адаптивно изменяют скорость обучения при
переменном шаге расчета.
Решение
проблемы
При обучении нейроидентификаторов
минимизируется ошибка
предсказания:
, (1)
где 
- ошибка предсказания;
- выходной сигнал
нейронной сети;
-выходной сигнал сложной технической установки.
В качестве функции критерия качества чаще всего берется сумма квадратов
ошибки предсказания. Для нейронных сетей с нелинейными функциями активации в
общем случае нельзя гарантировать достижения глобального минимума функции
ошибки. Графики функции ошибки 
могут иметь сложную
нелинейную форму с большим числом локальных миниумов 
(рис. 1). На поиск каждого минимума может быть
затрачено много времени, много циклов обучения нейронной сети. Нужно
добавить, что при размерности поискового пространства от 100 до 1000 количество
локальных минимумов для большинства практических задач обучения исчисляется
миллионами [1,2].
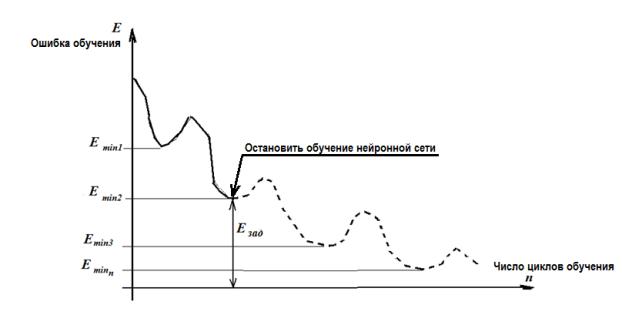
Рис. 1.
Ошибка обучения нейронной сети
Для
увеличения быстродействия работы нейроидентификаторов была разработана следящая система управления обучением нейронной сети
(рис. 2),
которая может следить за заданной точностью, отсекая поиск ненужных локальных
минимумов ошибки обучения.
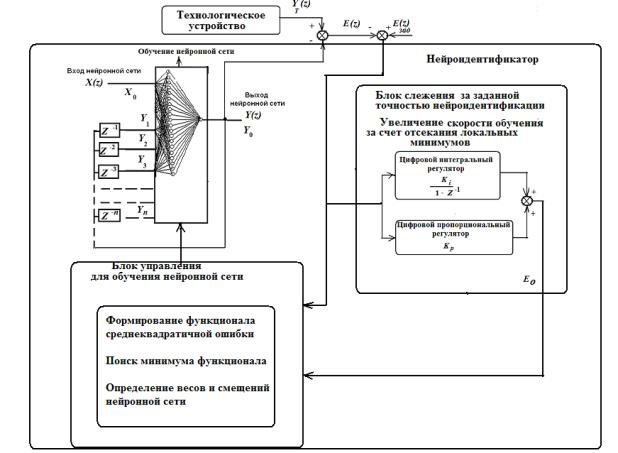
Рис. 2.
Структура нейроидентификатора со следящей системой управления обучением
нейронной сети
На рис. 2 элемент z в двухслойной нейронной сети осуществляет задержку сигнала на j шагов. На входы нейронной
сети подается X(z) сигнал управления и n значений сигнала с выхода
Y(z). Величина n определяется порядком
дифференциального уравнения, которое описывает работу электропривода. При этом используются два элемента входного
вектора: текущего выхода Y(n) и задержанного
выхода Y(n+1). Процедура идентификации
заключается в настройке весовых коэффициентов и параметров нейронов.
Настройка производится на основании информации о сигнале ошибки между выходом
технологического устройства и нейронной сети [3,4].
Система уравнений, описывающая работу рекуррентной нейронной
сети, имеют вид:
;
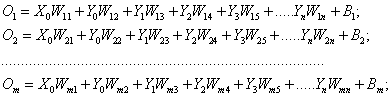
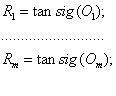(3)
где
- выходной сигнал нейронной сети; 
- входные сигналы
нейронной сети, задержанные на один, два, три,.. n количество тактов;
- выходные сигналы первого слоя нейронов; 
- веса первого слоя нейронов; 
- смещения первого слоя нейронов; 
- сигналы на выходе блоков активации первого слоя нейронов; 
- сигнал на выходе второго слоя нейронов; 
- веса второго слоя нейронов; 
- смещение второго слоя нейронов; 
- сигнал на выходе второго слоя нейронов, 
функция активации,
имеющая тангенциальную форму.
В нейронной сети используются
элементы входного вектора: 
текущего выхода 
и задержанного выхода
. Процедура
нейроидентификации технологического устройства заключается в настройке весовых
коэффициентов и параметров нейронов. Выходной сигнал с функциями активации типа 
для двухслойной
нейронной сети имеет вид:
,
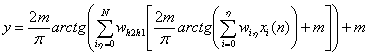(4)
где 
- входы нейронной сети; 
- выход нейронной сети; N- число входов нейронной сети; 
- вес к 
- му нейрону второго слоя от 
- го нейрона первого слоя сети; 
- смещение;
- вес обратной связи.
Оперативное обучение
веса связей нейронной сети корректируется на основе ошибки:
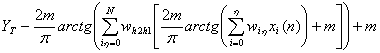. (5)
При оптимизации поиска
параметров нейронной сети используется функционал минимизации средней
квадратичной ошибки, который выглядит
следующим образом:
(6)
Параллельный алгоритм настройки двухслойной нейронной сети имеет вид:
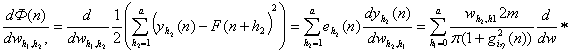
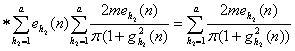, (7)
где 
- текущий момент времени; 
-выход второго слоя нейронов; 
- ошибка
решения во втором слое нейронов для текущего момента времени; 
- активация 
- слоя нейронов; 
- активации во втором
слое нейронов.
Веса нейронной сети в
процессе обучения корректируются по следующей формуле:
, (8)
где 
- коэффициент скорости обучения.
В процессе обучения нейронной сети
ошибка 
интегрируется, умножается на коэффициент интегральной составляющей
и коэффициент пропорциональной составляющей:
+ 
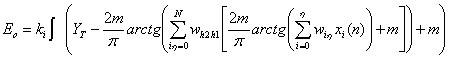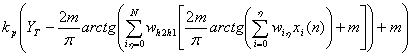. (9)
Сумма интегральной и пропорциональной составляющих 
поступает в блок
обучения нейронной сети. Цифровая следящая система работает до тех пор, пока не
будет достигнута заданная точность обучения нейронной сети. Цифровые регуляторы
обеспечивают точность и устойчивость следящей системы. Когда 
становится равна
, следящая система управления останавливает процесс обучения,
отсекая поиск ненужных локальных минимумов.
Другой,
предлагаемый в статье эффективный метод увеличения быстродействия работы нейроидентификаторов возможен
за счет динамического изменения величины шага обучения. Система управления состоит из блоков,
которые адаптивно изменяют скорость
обучения при переменном шаге расчета (рис.
3). Достигнуть минимума ошибки обучения можно при
постоянном и переменном шаге обучения. Однако, если в начале обучения нейронной
сети установить некоторое максимальное значение шага и, по мере приближения к
минимуму, шаг уменьшать, то можно резко уменьшить число эпох обучения поиска
минимума функционала оптимизации параметров нейронной сети. На рис. 4 представлены графики зависимости
ошибки обучения от числа эпох при переменном шаге расчета с отсеканием локальных минимумов, что
существенно уменьшает время работы
нейроидентификатора.
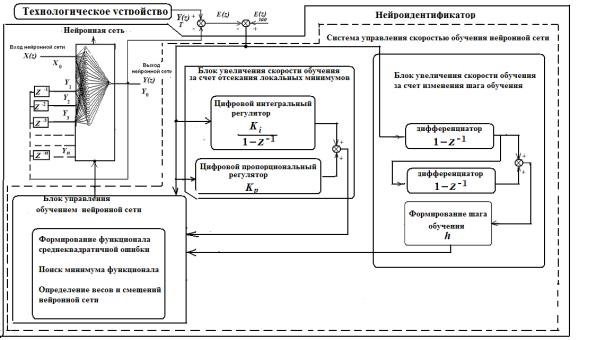
Рис. 3. Структурная схема нейроидентификатора с
блоками увеличения скорости обучения нейронной сети
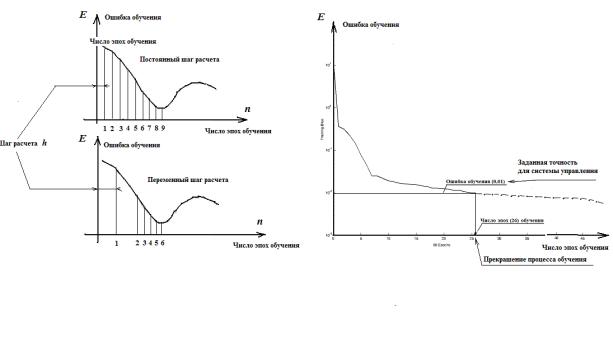Рис. 4. Графики зависимости ошибки обучения от числа
эпох при переменном шаге расчета с
отсеканием локальных минимумов,
В данном методе анализируется крутизна характеристики
ошибки обучения. На определенных этапах вычисляется первая и вторая производные
этой характеристики, которые осуществляют
динамическое управление шагом обучения
нейронной сетью по следующей формуле:
,
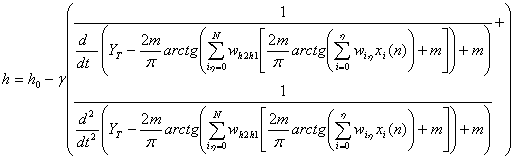(10)
где
-коэффициент масштабирования;
h - переменный
шаг расчета;
- постоянный шаг
расчета;
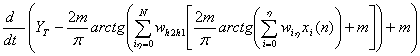- первая производная
ошибки обучения;
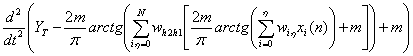- вторая производная ошибки обучения.
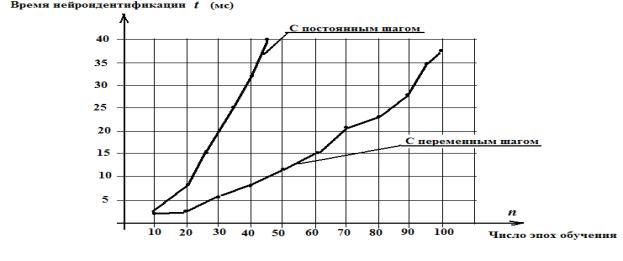
На рис. 5
изображены графики зависимостей времени нейроидентификации от числа эпох обучения при переменном шаге
расчета, из которых видно, что быстродействие обучения нейронной сети с переменным шагом расчета приблизительно
увеличивается в пять раз по сравнению с
постоянным шагом.
Рис.
5. Графики зависимостей времени
нейроидентификации от величины шага
расчета
Выводы
На
рис. 4. изображены графики зависимости
ошибки обучения от числа эпох при переменном шаге расчета с отсеканием локальных минимумов, что
существенно уменьшает время работы
нейроидентификатора. На рис. 5.
изображены графики зависимостей времени нейроидентификации от числа эпох обучения при переменном шаге
расчета, из которых видно, что быстродействие обучения нейронной сети с переменным шагом расчета приблизительно
увеличивается в пять раз по сравнению с
постоянным шагом.
Литература:
1. Буянкин, В. М. Применение
искусственной нейронной сети в режиме идентификации динамических параметров
электродвигателя // Вестник МГТУ им. Н.Э. Баумана. Сер.
«Приборостроение».― 2006. ― №3. ― С. 25―30.
2.Буянкин
В.М. Нейронные сети в управлении.
Издание
LAMBERN Academic Publishing Germany,
2011г 265 С.
,
3. Буянкин, В.М. Нейроидентификация
физических процессов при ионно-плазменном напылении // Нейроинформатика-2009:
труды 11-й Всероссийской научно-технической конференции. ― Москва, 2009.
―
С. 58―65.
4.Буянкин, В.М. Разработка метода синтеза
многопараметрической нейропрогнозирующей идентификации с использованием
ансамбля нейронных сетей с нечеткой логикой для сложных технологических
установок // Промышленные АСУ и
контроллеры. ― 2012. ― №6. ―
С. 31―35.
,