Математика/ 4.Прикладная математика

К.ф.м.н., доцент Абатов Н.Т.

Костанайский государственный университет имени А.Байтурсынова,

Казахстан

Об области определения некоторых функции

Выпускники школ затрудняются при поиске области определения некоторых сложных функции. Поэтому рассмотрим такие задачи и укажем способы ихрешения.

№1. Найдите область определения функции

.

Решение. Область определения данной функции должна удовлетворять условию

.

Это - тригонометрическое неравенство. Применяем формулу

.

Тогда имеем:

Введем замену . Тогда получаем квадратное неравенство

Применяем метод интервалов. Тогда множество -0,5 ≤ y ≤ 1 является решением квадратного неравенства

Произведем обратную замену . Тогда получаем:0,5 ≤ ≤ 1.

Это двойное неравенство равносильно неравенству . Решением этого неравенства является множество

.

Итак, областью определения исходной функций является вышеуказанноемножество.

Ответ:

№2.Найдите область определения функции

.

Решение. Область определения данной функции должна удовлетворять условии Это тригонометрическое неравенство. Применяем формулу .

Тогда имеем:

Введем замену Тогда получаем квадратное неравенство

Применяем метод интервалов. Тогда множество 0,5 ≤ y ≤ 1 является решением квадратного неравенства .

Произведем обратную замену Тогда имеем: 0,5 ≤ sinx ≤ 1.

Это двойное неравенство равносильно неравенству . Решением этого неравенства является множество

.

Это множество является областью определения исходной функции.

Ответ:.

№3. Найдите область определения функции

.

Решение. Область определения функции должна удовлетворять условиям:

Функция положительна в первом и в четвертом четвертях. Кроме этого учтем, что .

Тогда множество

.

является областью определения исходной функции.

Ответ:

№4. Найдите область определения функции

.

Решение. Область определения данной функции должна удовлетворять условиям:

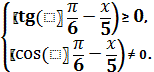
Решаем тригонометрическое неравенство

Функция принимает отрицательные значения во второй и в четвертой четвертях. Поэтому, с учетом условия , имеем:

Итак, множество.

является областью определения исходной функции

Ответ:.

№5. Найдите область определения функции

.

Решение. Область определения данной функции должна удовлетворять условию:

Это тригонометрическое неравенство. Умножаем на число обе части данного неравенства.

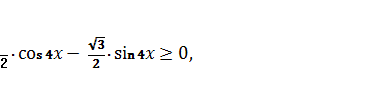
Применяем формулу

Тогда имеем: .

Функция положительна в первых и в четвертой четвертях. Поэтому имеем:

Итак, множество

.

является областью определения исходной функции

Ответ:

Литература

1. Абатов Н.Т. Методы решения задач по математике. Алгебра. Учебное пособие для поступающих в ВУЗы. – Костанай, 1998г.

2. Потапов М.К., Олехник С.Н., Нестеренко Ю.В. Конкурсные задачи по математике. Справочное пособие. – Москва, 1995г.