Математика/4.Прикладная математика

O.F. Ryaboshtan, Ph.D. A.M. Milenin, Ph.D. S.M. Skofenko

Kharkov National Technical University of Agriculture after P. Vasilenko

Differential equations manifold surface of gas turbine blades

Consider the set of surfaces

, (1)

where the - factors that affect both the shape and the position of the turbine blades.

Try to determine the differential equation of all varieties envelope surfaces, which can be obtained from a given - parametric set. Differentiating (1) with respect and

(2)

For the two-parameter set (1) is sufficient (1) and (2) delete parameters and . We obtain the differential equation in partial derivatives of order I, for which (1) is a complete integral. To obtain equation containing only variables , , and the partial derivatives , , , , need to equations (2) to apply well-known algorithm and equate

(3)

And see equations (1) - (3) together.

In more detail, equation (3) has the form:

. (4)

At  equation (3) to differentiate to the desired number of times until the number of equations (together with (1) - (3)) will be . From the resulting system of equations exclude coefficients To give the desired differential equation.

However, in many cases, the design of engineering surfaces do not need to search for an equation that does not contain parameters . On the contrary, the parameters must be secured in order to meet given geometric conditions, and differential equations need to make such an order, given what extent differential conditions.

At that time, when the differential equation which does not contain for this (1), is the only equations with parameters, you can obtain an infinite set.

For example, for a plurality of areas of constant radius

(5)

have

, (6)

from where

(7)

or

(8)

The differential equation for (5), does not contain the coefficients has the form:

(9)

and expresses the differential conditions for all of canal surfaces radius .

For a set of conical surfaces

. (10)

The only differential equation that does not contain the coefficients has the form:

. (11)

For a set of conical surfaces of revolution

(12)

Partial differential equation that does not contain the coefficients , , is

(13)

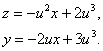(14)

To determine the edge of regression, it is necessary from the equations (14) to differentiate and the resulting equation for considered in conjunction with (14).

, . (15)

Above the surface of the blades allows the construction of raised their special lines (curvature, transition, etc.). In this case, as previously indicated, it is necessary to take appropriate equipment curve and apply equation (13).

We consider the problem of constructing the blade surface, which passes into the surface of the hub

, . (16)

It is assumed that there are a lot of planes, moving from to .

Is the condition of tangency of the plane (1) to the surface (16)

, , (17)

, . (18)

Ruling out , , (coordinates of the point of contact with the surface ) (1) and (17) we obtain the dependence

(19).

Similarly, from (1) and (18)

(20)

Considering together (19) and (20), determines the dependence of the two factors in the third example

, . (21)

Substitute in (1) and determines the desired surface envelope of the set of planes (1) with (21).

Note that the above algorithms can refuse in some cases more simple compared to previously developed. A common drawback is the complexity of analytic transformations, difficulties with the exclusion of parameters. The way out of this difficulty can be:

- go to the interpolation and approximating methods;

- develop a method elementating design, widespread problems in the surface profiling of gas turbine blades .