Математика/4. Прикладная математика
К.ф.-м.н. Зинченко А.Б., Глыбин Г.Ю., Аль Джабери Х.С.
Южный федеральный университет. Россия
Двухэтапные решения кооперативной CS-игры
Кооперативная игра с коалиционной
структурой (![]() -игра)
-игра) ![]() состоит из классической
игры
состоит из классической
игры ![]() , где
, где ![]() ,
, ![]() ,
, ![]() ,
, ![]() , и коалиционной структуры
, и коалиционной структуры
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Предполагается, что структура ![]() сформировалась до
начала игры. Структурная компонента
сформировалась до
начала игры. Структурная компонента ![]() , называемая союзом (union), отличается от стандартной коалиции
, называемая союзом (union), отличается от стандартной коалиции ![]() тем, что союз
действует как единый игрок, т.е. образование подкоалиций
тем, что союз
действует как единый игрок, т.е. образование подкоалиций ![]() запрещено правилами
игры.
запрещено правилами
игры.
Коалиционный
оператор значения ![]() (
(![]() -оператор) ставит в соответствие каждой игре
-оператор) ставит в соответствие каждой игре ![]() вектор
вектор ![]() выигрышей агентов (
выигрышей агентов (![]() -значение).
-значение).
Понятие ![]() -игры было введено в [1]. Решение
-игры было введено в [1]. Решение ![]() , предложенное Ауманном и Дрезом,
обобщает значение Шепли
, предложенное Ауманном и Дрезом,
обобщает значение Шепли ![]() . Оно компонентно-эффективно
. Оно компонентно-эффективно ![]()
![]() ,
, ![]() .
.
![]() -игра
-игра ![]() распадается
распадается ![]() игр
игр
![]() ,
, ![]() ,
, ![]() , (1)
, (1)
внутри союзов ![]() и
и ![]() для всех
для всех ![]() . Игра
. Игра ![]() , являющаяся ограничением исходной игры
, являющаяся ограничением исходной игры ![]() , не учитывает "внешние" возможности участников
союза
, не учитывает "внешние" возможности участников
союза ![]() и способ разбиения остальных
агентов
и способ разбиения остальных
агентов ![]() .
.
Эффективное
![]() -значение реализует другой сценарий: разыгрывается внешняя
игра
-значение реализует другой сценарий: разыгрывается внешняя
игра
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
(2)
,
(2)
дележа ![]() между компонентами структуры
между компонентами структуры ![]() и внутренние игры между
партнерами каждого союза
и внутренние игры между
партнерами каждого союза ![]() . Первое эффективное
. Первое эффективное ![]() -значение
-значение ![]() , предложенное Оуэном [2], использует
во внешней и внутренних играх значение Шепли. При вычислении
, предложенное Оуэном [2], использует
во внешней и внутренних играх значение Шепли. При вычислении ![]() внутренние (редуцированные)
игры
внутренние (редуцированные)
игры ![]() имеют более сложный
вид, чем (1). Вес
имеют более сложный
вид, чем (1). Вес ![]() каждой коалиции
каждой коалиции ![]() равен ее выигрышу во
вспомогательной игре
равен ее выигрышу во
вспомогательной игре ![]() между компонентами
структуры
между компонентами
структуры ![]() , полученной из
, полученной из ![]() удалением игроков
принадлежащих
удалением игроков
принадлежащих ![]() ,
,
![]() ,
, ![]() ,
,
где ![]() для
для ![]() ,
, ![]() для остальных
для остальных ![]() . Таким образом, при дележе выигрыша, полученного союзом
. Таким образом, при дележе выигрыша, полученного союзом ![]() во внешней игре,
используются модифицированные веса коалиций
во внешней игре,
используются модифицированные веса коалиций ![]() .
.
После ![]() были введены и
аксиоматизированы алогичные
были введены и
аксиоматизированы алогичные ![]() -значения, сочетающие
-значения, сочетающие ![]() с взвешенным значением
Шепли, значением Банзафа [3], консенсус-значением [4-6]. Эффективные
с взвешенным значением
Шепли, значением Банзафа [3], консенсус-значением [4-6]. Эффективные ![]() -значения подходят для игр
-значения подходят для игр ![]() , удовлетворяющих условию
, удовлетворяющих условию
![]() , (3)
, (3)
а компонентно-эффективные ![]() -значения – для игр, удовлетворяющих противоположному
неравенству.
-значения – для игр, удовлетворяющих противоположному
неравенству.
Большинство
![]() -значений удовлетворяет аксиоме нулевого игрока: агент
-значений удовлетворяет аксиоме нулевого игрока: агент ![]() , присоединение которого к любой коалиции
, присоединение которого к любой коалиции ![]() , не увеличивает прибыль партнеров, получает нулевой выигрыш.
Этот "жесткий" принцип не всегда сочетается с моделируемой ситуацией [7].
, не увеличивает прибыль партнеров, получает нулевой выигрыш.
Этот "жесткий" принцип не всегда сочетается с моделируемой ситуацией [7].
Данная статья посвящена сравнению двух CS-значений,
не удовлетворяющих аксиоме нулевого игрока: двухэтапного значения Шепли [8] и
двухэтапного консенсус-значения [9]. Оба решения были предложены недавно и еще
недостаточно исследованы. Формулируются необходимые и достаточные условия, при
которых нулевой агент получает положительный выигрыш. Доказывается, что
двухэтапное значение Шепли может не принадлежать не только непустому С-ядру, но и множеству дележей. Вводится
новая аксиома для двухэтапного консенсус-значения.
Двухэтапное значение Шепли ![]() определяется формулой
определяется формулой
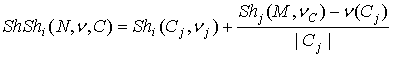 ,
, ![]() . (4)
. (4)
Внешняя игра ![]() для
для ![]() такая же, как и для
значения Оуэна. Внутренние игры
такая же, как и для
значения Оуэна. Внутренние игры ![]() аналогичны играм (1), использующимся при вычислении
значения Ауманна-Дреза. Двухэтапное значение Шепли однозначно определяется
тремя стандартными для
аналогичны играм (1), использующимся при вычислении
значения Ауманна-Дреза. Двухэтапное значение Шепли однозначно определяется
тремя стандартными для ![]() -значения
-значения ![]() аксиомами эффективности
EF, аддитивности AD, внешней (коалиционной) симметричности CSy и двумя
дополнительными аксиомами, сформулированными в [8].
аксиомами эффективности
EF, аддитивности AD, внешней (коалиционной) симметричности CSy и двумя
дополнительными аксиомами, сформулированными в [8].
(IE) Внутреннее равенство. Если агенты ![]() симметричны в игре
симметричны в игре
![]() , то
, то ![]() .
.
(CNP) Свойство коалиционного
нулевого игрока. Если ![]() нулевой агент в
нулевой агент в ![]() , а союз
, а союз ![]() - нейтральный игрок в
- нейтральный игрок в
![]() , то
, то ![]() .
.
Двухэтапное консенсус-значение ![]() определяется формулой
определяется формулой
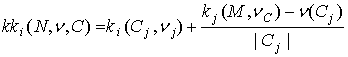 ,
, ![]() , (5)
, (5)
где
![]() ,
, ![]() , (6)
, (6)
и отличается от двухэтапного значения Шепли тем, что в
(4) значение Шепли заменено консенсус-значением [10]. Двухэтапное
консенсус-значение является единственным ![]() -значением, удовлетворяющий аксиомам аддитивности, внешней симметричности,
внутренней симметричности и следующим двум аксиомам.
-значением, удовлетворяющий аксиомам аддитивности, внешней симметричности,
внутренней симметричности и следующим двум аксиомам.
(F) Допустимость. ![]() .
.
(MCNP) Модифицированное свойство коалиционного нулевого игрока. Если ![]() нулевой агент в
нулевой агент в ![]() , а союз
, а союз ![]() - нейтральный игрок в
- нейтральный игрок в
![]() , то
, то
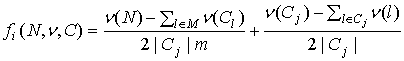 .
.
Известно,
что значение Шепли может не принадлежать не только непустому ![]() -ядру
-ядру ![]() , но и непустому множеству дележей
, но и непустому множеству дележей ![]() . Покажем, что это свойство
сохраняется и для
. Покажем, что это свойство
сохраняется и для ![]() , а
, а ![]() реже, чем
реже, чем ![]() , не принадлежит
, не принадлежит ![]() .
.
Теорема 1. Пусть игра ![]() 0-нормализованна,
удовлетворяет (3) и
0-нормализованна,
удовлетворяет (3) и ![]() для всех
для всех ![]() . Если
. Если ![]() и
и ![]() , то
, то ![]() , но обратное не верно.
, но обратное не верно.
Доказательство. Выразим вначале ![]() через
через ![]() . Возьмем
. Возьмем ![]() . Из 0-нормализованности игры
. Из 0-нормализованности игры ![]() и формул (5)-(6) следует
и формул (5)-(6) следует
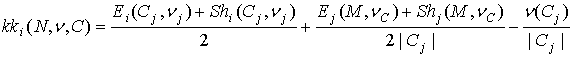 ,
,
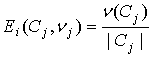 ,
, 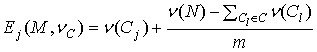 .
.
Получаем
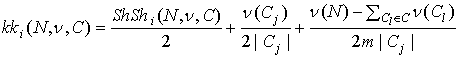 . (7)
. (7)
Для 0-нормализованной игры, ![]() . По предположению
. По предположению ![]() . Значит,
. Значит, ![]() для всех
для всех ![]() . Из последнего неравенства, (3), (7) и
. Из последнего неравенства, (3), (7) и ![]() ,
, ![]() , имеем
, имеем ![]() ,
, ![]() . По аксиоме эффективности
. По аксиоме эффективности ![]() . Получили, что
. Получили, что ![]() . Рассмотрим теперь игру
. Рассмотрим теперь игру ![]() , где
, где ![]()
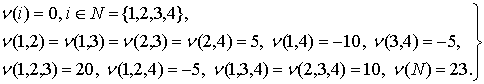 (8)
(8)
Из ![]() следует
следует ![]() . Данная игра удовлетворяет всем предположениям теоремы. Двухэтапное
значение Шепли
. Данная игра удовлетворяет всем предположениям теоремы. Двухэтапное
значение Шепли ![]() не принадлежит множеству
дележей. Подставив
не принадлежит множеству
дележей. Подставив ![]() в (7), получаем
в (7), получаем ![]() . ÿ
. ÿ
Обозначим
через ![]() и
и ![]() множества нулевых и
нейтральных агентов игры
множества нулевых и
нейтральных агентов игры ![]() . Следующая теорема содержит условия, при которых нулевой
агент
. Следующая теорема содержит условия, при которых нулевой
агент ![]() получает (в классе
0-нормализованных
получает (в классе
0-нормализованных ![]() -игр) положительный выигрыш
-игр) положительный выигрыш ![]() или
или ![]() .
.
Теорема
2. Пусть игра ![]() имеет 0-форму. Если
имеет 0-форму. Если ![]() нулевой агент в
нулевой агент в ![]() , то
, то
-
![]() тогда и только тогда,
когда
тогда и только тогда,
когда ![]() ;
;
-
![]() тогда и только тогда,
когда
тогда и только тогда,
когда 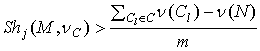 .
.
Доказательство.
Нулевой с исходной игре агент ![]() будет также нулевым в
игре внутри союза
будет также нулевым в
игре внутри союза ![]() . Согласно аксиоме нулевого игрока и определению игры
. Согласно аксиоме нулевого игрока и определению игры ![]() , Шепли-выигрыш
, Шепли-выигрыш ![]() агента
агента ![]() равен нулю. Значит,
равен нулю. Значит, 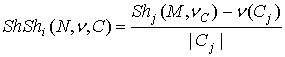 , т.е. справедливо первое утверждение теоремы. Подставив
выражение для
, т.е. справедливо первое утверждение теоремы. Подставив
выражение для ![]() в (7), поучаем
в (7), поучаем
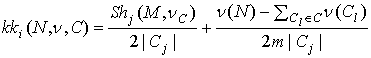 ,
,
т.е. справедливо второе утверждение. ÿ
В [11]
предложена новая аксиоматизация двухэтапного значения Шепли, использующая EF, AD, CSy и
следующие три аксиомы.
(NC) Свойство
нулевой коалиции. Если ![]() - нулевой игрок в
- нулевой игрок в ![]() , то
, то ![]() .
.
(Coh) Согласованность.
![]() , где
, где ![]() и
и ![]() - тривиальные
коалиционные структуры.
- тривиальные
коалиционные структуры.
(PS) Солидарность
внутри союза. Для любых![]()
![]() и
и ![]() ,
, ![]() ,
,
![]() ,
,
где ![]() .
.
Для
описания аналогичных свойств двухэтапного консенсус-значения, введем новую
аксиому.
(MNC) Модифицированное
свойство нулевой коалиции. Если ![]() , то
, то ![]() .
.
Теорема 3. Двухэтапное
консенсус-значение ![]() удовлетворяет
аксиомам Coh, PS и MNC, но не удовлетворяет аксиоме NC .
удовлетворяет
аксиомам Coh, PS и MNC, но не удовлетворяет аксиоме NC .
Доказательство. Для ![]() , внешняя игра
, внешняя игра ![]() состоит из одного
игрока
состоит из одного
игрока ![]() , поэтому
, поэтому ![]() , а внутренняя игра
, а внутренняя игра ![]() совпадает с
совпадает с ![]() . Значит,
. Значит, ![]() ,
, ![]() . Из формулы (5) получаем
. Из формулы (5) получаем ![]() . Если
. Если ![]() , то внешняя игра
, то внешняя игра ![]() совпадает с
совпадает с ![]() , поэтому
, поэтому ![]() ,
, ![]() . Все внутренние игры
. Все внутренние игры ![]() ,
, ![]() , состоят из одного агента. Значит,
, состоят из одного агента. Значит, ![]() ,
, ![]() . Окончательно,
. Окончательно, ![]() , т.е. справедлива аксиома Coh. Пусть
, т.е. справедлива аксиома Coh. Пусть ![]() и
и ![]() ,
, ![]() , тогда по формуле (5)
, тогда по формуле (5)
![]() ,
,
где ![]() , если
, если ![]() ,
, ![]() в противном случае. Очевидно, последнее выражение равно
в противном случае. Очевидно, последнее выражение равно ![]() , т.е.
, т.е. ![]() удовлетворяет аксиоме
PS. Из (5) следует
удовлетворяет аксиоме
PS. Из (5) следует
![]() ,
, ![]() .
.
Консенсус-значение
удовлетворяет аксиоме эффективности, поэтому
![]()
![]() .
.
Если ![]() , то
, то ![]() и
и ![]() . Значит,
. Значит,
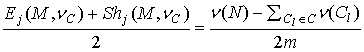 ,
,
т.е. ![]() удовлетворяет аксиоме
MNC. Рассмотрим теперь игру
удовлетворяет аксиоме
MNC. Рассмотрим теперь игру ![]() :
:
![]() ,
, ![]() ,
, ![]() ,
, ![]() для остальных
для остальных ![]() .
.
Четвертый агент – нулевой в ![]() , а также является одноэлементной компонентой
, а также является одноэлементной компонентой ![]() данной структуры.
данной структуры. ![]() - нулевой, а также нейтральный
игрок во внешней игре
- нулевой, а также нейтральный
игрок во внешней игре ![]() . По аксиоме MNC,
. По аксиоме MNC, ![]() , т.е.
, т.е. ![]() не удовлетворяет аксиоме
NC. ÿ
не удовлетворяет аксиоме
NC. ÿ
Литература:
1.
Aumann R.J., Dreze J.H. Cooperative Games with
Coalition Structure // International Journal of Game Theory. 1974. N. 3. P.
217-237.
2.
Owen G. Values of games with a priory unions. Essays
in mathematical economics and game theory. Berlin, 1977, pp. 76-88.
3.
Gomez-Rua M., Vidal-Puga J. The axiomatic approach to
three values in games with coalition structure // MPRA paper. 2008. N. 8904. P.
1-30.
4.
Зинченко А.Б., Мироненко
Г.В., Провоторова П.А. Консенсус-значение для игр с коалиционной структурой //
Математическая теория игр и ее приложения. Том 2. Выпуск 1. 2010. С. 93-106.
5.
Zinchenko A.B., Provotorova P.A., Mironenko G.V. Efficient CS-values
based on consensus and Shapley values // Contributions to Game Theory and
Management. Vol. 4. 2011. P. 502-513.
6.
Зинченко А.Б. Аксиоматическое
обоснование новых операторов значения для игр с коалиционной структурой //
Известия вузов. Сев.-Кавказ. регион. Естественные науки. 2011. № 1. С. 5-8.
7.
Van den Brink R. Null or nullifying players: the
difference between the Shapley value and equal division solutions // Journal of
Economic Theory. 2007. Vol. 136. P. 767-775.
8.
Kamijo Y. A two-step Shapley value for cooperative
games with coalition structures // International Game Theory Review. 2009. Vol.
11. P. 207-214.
9.
Зинченко А.Б. Двухэтапный
CS-оператор, использующий консенсус-значение // Известия вузов. Сев.-Кавказ. регион.
Естественные науки. 2013. № 4. С.10-13.
10.
Ju Y., Born P., Rays P. The consensus value: a new
solution concept for cooperative games // Social Choice and Welfare. 2006. Vol.
28. N. 4. P. 85-703.
11.
Calvo E., Gutierrez M.E. Solidarity in games with a
coalition structure // Discussion Papers in Economic Behaviour from University of Valencia. N.
810. 2010. P. 1-22.