Хомченко А. Н.

Черноморский государственный университет им. Петра Могилы,
г. Николаев, Украина

ФУНКЦИЯ – «ПАГОДА»: ИЗВЕСТНАЯ И НЕИЗВЕСТНАЯ.

Введение. Функция – «пагода» (термин Г. Стренга и Дж. Фикса [1]) представляет собой произведение Х ()  Y (y) двух основных кусочно-линейных функций – «крышек» одной переменной. Она успешно применяется в методе конечных элементов (МКЭ) для решения двумерных задач. Прообразом «пагоды» была известная пирамида Куранта (1943 г.), с которой начиналась история развития МКЭ. Носитель функции Куранта (ячейка Куранта) состоит из шести самостоятельных прямоугольных треугольников. Каждый треугольник «несёт» линейную функцию (фрагмент плоскости). Носитель «пагоды» состоит из восьми попарно «сшитых» прямоугольных треугольников, т. е. из четырёх самостоятельных квадратов. Каждый квадрат «несёт» нелинейную функцию (фрагмент гиперболического параболоида – гипара). Пирамида Куранта опирается на 6 симплексов, а «пагода» – на 4 мультиплекса (по терминологии Дж. Одена [2]). Поскольку все фрагменты «пагоды» одинаковы, достаточно рассматривать один фрагмент. Это специально вырезанная часть поверхности гипара с квадратным планом. Именно на этом фрагменте мы сосредоточим наше внимание. С точки зрения новых знаний небольшой ограниченный фрагмент намного содержательнее безграничной поверхности гипара. Главная особенность «пагоды» состоит в её финитности, т. е. в том, что она обращается в нуль всюду, кроме четырёх квадратных ячеек, на которые делится расчётная область.

Анализ предшествующих публикаций. Систематическое изучение и широкое применение гипаров в качестве оболочечных элементов инженерных сооружений началось в 30-е годы прошлого века [3]. Впервые автору посчастливилось узнать о необыкновенных свойствах гипара в начале
70-х годов ХХ столетия в связи с исследованиями по колебаниям и изгибу оболочек [4-6]. Во второй половине ХХ века гипары привлекли внимание многочисленных разработчиков и пользователей МКЭ [1, 2, 4, 5] в связи с задачей билинейной интерполяции функций двух аргументов. В начале
80-х годов ХХ века, когда стало понятно, что роль матричной алгебры в МКЭ преувеличена, появились геометрические подходы [6], а также стохастические процедуры моделирования КЭ [7, 8]. О способах построения функции – «пагоды» можно прочитать в [9].

Цель статьи – описать малоизвестные и неизвестные свойства «пагоды», т. е. базисной функции билинейной интерполяции.

Основная часть. Наиболее общий метод использования четырехугольных КЭ состоит в применении точечного преобразования четырехугольника в квадрат и в использовании изопараметрической аппроксимации [4, 5] (В. Irons, 1966). Если расчетные узлы (рис. 1) расположены в вершинах квадрата: то базис билинейной аппроксимации имеет вид [2]:

(1)

Эти функции обладают следующими свойствами:

(2)

где і – номер функции, – номер узла.

4

3

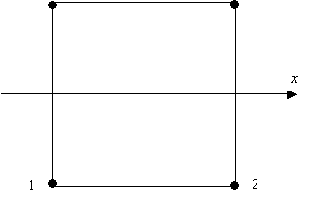
Рис. 1. Элемент билинейной интерполяции

Заметим, что эти свойства можно истолковать в терминах теории вероятностей, что позволяет предложить вероятностно-геометрический способ конструирования базисов КЭ [7-9]. C геометрической точки зрения каждая функция (1) представляет собой фрагмент поверхности гипара с наивысшей точкой в «своём» узле. Если собрать 4 квадрата так, чтобы наивысшие точки гипаров совпали в центре, получим «пагоду» (рис. 2).

Представляет интерес тестирование функции на гармоничность. Оказывается, эта функция выдерживает тестирование по трём критериям гармоничности. Напомним эти критерии:

дифференциальный критерий Лапласа (1782):

(3)

интегральный критерий Кёбе (1906):

(4)

где левая часть – среднее интегральное (по периметру области D) значение правая часть – значение функции в барицентре квадрата;

интегральный критерий Привалова (1925):

(5)

где левая часть – среднее интегральное (по площади области D) значение

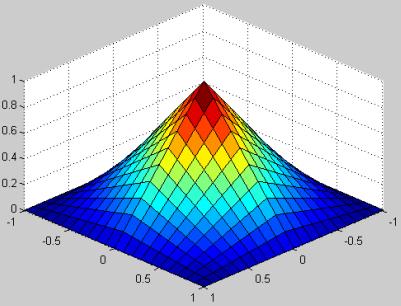
Рис. 2. Функция – «пагода»

Теперь рассмотрим тело, заключенное между областью и поверхностью Найдём точное значение объёма этого клиновидного тела:

. (6)

Теперь вычислим приближенно по формуле Симпсона (правило трёх параллельных сечений, 1743). Здесь важно правильно (рационально) выбрать параллельные сечения (два опорных и среднее). Вычисления существенно упрощаются, если выбрать вертикальные сечения, параллельные координатной плоскости, например: – опорные и – среднее.

Тогда (7)

где и и – площади соответствующих сечений.

То, что приближённая формула Симпсона даёт точное значение объёма, означает, что тело, ограниченное «пагодой», относится к семейству симпсоновых тел.

Нетрудно установить, что «пагода» принадлежит семейству коноидов. Достаточно вспомнить определение: коноид – линейчатая поверхность, все прямолинейные образующие которой параллельны одной и той же плоскости и пересекают одну и ту же прямую (ось коноида). Выходит, что «пагода» – это двухосный коноид с ортогональными осями.

Наконец, вернёмся к вероятностному содержанию . Свойства (2) позволяют сформулировать в мультиплексе правила одношаговых 4-маршрутных «блужданий» частицы со случайным стартом . Кавычки означают, что частица не блуждает, а всего за один шаг переходит с вероятностью в поглощающую вершину квадрата .

Анализируя вероятностные свойства и одношаговую схему «блуждений», мы приходим к обратной задаче, т. е. к задаче о случайно вложенных квадратах. Сначала рассмотрим концентрическое вложение. На рис. 3 изображён случайный квадрат , который наугад вложен в основной квадрат так, что их барицентры совпадают (концентрическое вложение).

А4
		А3

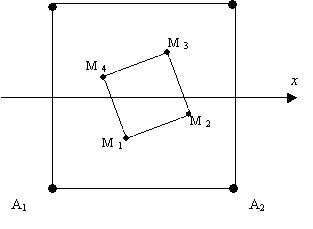
Рис. 3. Случайное концентрическое вложение

Обозначим вероятность перехода частицы из вершины вложенного квадрата в вершину основного квадрата через Легко проверить, что известное свойство (2) билинейного базиса обретает вид:

– фиксировано. (8)

Это своеобразное обобщение (адаптирование) известного шаблона типа «крест» (один старт и четыре финиша). Читатель может аналитически, графически или экспериментально доказать, что при концентрическом вложении сохраняется баланс переходных вероятностей для всех траекторий, начинающихся в случайных вершинах и оканчивающихся в фиксированной вершине :

– фиксировано. (9)

Это «обратная» схема (четыре старта и один финиш). Нетрудно догадаться, что при эксцентрическом вложении случайного квадрата формула (8) не изменится. А что произойдет с формулой (9)? Как модифицировать модель концентрического вложения, если диаметр вложенного квадрата превзойдёт диаметр основного квадрата?

В МКЭ считается, что базисная функция за пределами носителя равна нулю, а в задаче о случайно вложенных фигурах можно отказаться от этого ограничения и поэкспериментировать.

Выводы. Функция – «пагода» не так проста, как кажется на первый взгляд. Нетрудно предположить, что задача о вложениях случайного куба в основной куб приведёт к новым свойствам базиса трилинейной интерполяции.

Литература

1. Стренг Г. Теория метода конечных элементов / Г. Стренг, Дж. Фикс. – М. : Мир, 1977. – 350 с.

2. Оден Дж. Конечные элементы в нелинейной механике сплошных сред / Дж. Оден. – М. : Мир, 1976. – 464 с.

3. Рассказов А. О. Расчёт оболочек типа гиперболических параболоидов / А. О. Рассказов. – К. : КГУ, 1972. – 175 с.

4. Хомченко А. Н. О собственных колебаниях асимгиполоида, несущего локально присоединённую массу / А. Н. Хомченко // Труды НКИ. – Николаев : НКИ, 1971. – Вып. 46. – 1971. – С. 130–136.

5. Калько А. М. О напряжённо-деформированном состоянии ортотропной оболочки постоянного кручения / А. М. Калько, А. Н. Хомченко // Труды НКИ. – Вып. 56. – Николаев : НКИ, 1972. – С. 43–46.

6. Хомченко А. Н. Нелинейные колебания оболочки типа гиперболический параболоид / А. Н. Хомченко // Труды НКИ. – Вып. 90. – Николаев : НКИ, 1974. – С. 48–53.

7. Марчук Г. И. Введение в проекционно-сеточные методы / Г. И. Марчук, В. И. Агошков. – М. : Наука, 1981. – 416 с.

8. Зенкевич О. Метод конечных элементов в технике / О. Зенкевич. – М. : Мир, 1975. – 541 с.

9. Wachspress E. L. A rational finite element basis / E. L. Wachspress. – Academic Press. – New York, 1975. – 216 p.

10. Хомченко А. Н. Некоторые вероятные аспекты МКЭ / А. Н. Хомченко. – Ив.-Франк. ин-т нефти и газа. – Ивано-Франковск, 1982. – 9 с. Деп. в ВИНИТИ 18.03.82, № 1213.

11. Хомченко А. Н. Метод конечных элементов: стохастический подход / А. Н. Хомченко. – Ив.-Франк. ин-т нефти и газа. – Ивано-Франковск, 1982. – 7 с. Деп. в ВИНИТИ 15.10.82, № 5167.

12. Хомченко А. Н. П’ять способів побудови функції – «пагоди» / А. Н. Хомченко, І. О. Астіоненко, Н. О. Козуб // Прикладна геометрія та інженерна графіка. Праці / Тавр. держ. агротехнол. ун-т. – Вип. 4. Т. 37. – Мелітополь : ТДАТУ, 2008. – С. 24–31.