Математика/5. Математическое моделирование

К.т.н., доцент Кабулова Е.Г.

Старооскольский технологический институт им. А.А. Угарова (филиал) «Национального исследовательского технологического университета «Московский институт стали и сплавов», Россия

Многоуровневая система моделей подсчета запасов железной руды в металлургической отрасли

Совершенствование методов подсчета запасов железной руды является весьма актуальным вопросом на современном этапе развития металлургической промышленности. Знание промысловых параметров карьеров и рудников позволяет прогнозировать разработки месторождений и эффективно управлять данным процессом.

В нашей стране оценивание запасов производится в основном с использованием детерминированных методов, а итоговая оценка является точечной. Лишь для расчета отдельных параметров в моделях используются статистические методы, различные методы усреднения и взвешивания [1]. В то же время в США, Японии и других зарубежных странах запасы железной руды определяются и утверждаются в виде функций распределения вероятности [5]. Однако данных для построения функций распределения вероятностей по каждому параметру бывает недостаточно. К тому же операции с этими функциями в теории вероятностей очень громоздки

Погрешность различных приборов и датчиков, проводимых исследований, наличие по целому ряду параметров возможности лишь косвенной их оценки приводят к необходимости проведения расчетов при наличии неточно заданных параметров и коэффициентов уравнений. Замена неточных величин на детерминированные приводит к необходимости их итерационного подбора для получения приемлемых результатов [3].

В этом случае также затруднена оценка погрешности получаемого результата. Очень часто в состав параметров и коэффициентов уравнений входят одновременно величины с различным характером неопределенности: интервальные, нечеткие, стохастические, эвристические. Поэтому возникает необходимость представления всей информации на едином формальном языке теории нечетких множеств с представлением характеристик неточно заданных величин в виде F-функций [2].

Интерпретация неопределенных величин как нечетких больше соответствует реальной промысловой ситуации по сравнению с интерпретацией этих величин как случайных. Применение для оперирования с неопределенными величинами аппарата теории вероятности приводит к тому, что фактически неопределенность независимо от ее природы отождествляется со случайностью, между тем как основным источником неопределенности во многих процессах принятия решений может являться нечеткость.

Для подсчета запасов железной руды воспользуемся известным уравнением [4]:

(1)

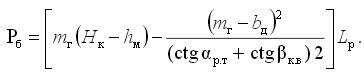
где L_p - длинна залежи по простиранию, m_г - горизонтальная мощность рудного тела, b_д - ширина дна карьера; Н_к – базовая глубина карьера; h_м - вертикальная мощность наносов; α_р.т. – угол падения залежи; β_к.в. – угол наклона борта карьера.

В отличие от существующей практики предварительного получения точечных оценок для каждого параметра на основе различных способов усреднения, взвешивая по объему и площади в предлагаемом подходе каждый из них задается в виде соответствующей функции принадлежности µ(h), µ(α), µ(β), µ(m).

Результирующую функцию принадлежности для запасов руды получаем из уравнения (1) с учетом определения алгебраических операций:

(2)

где _.

Решение задачи (2) аналитическими методами, описанными выше, довольно затруднительно, поэтому на практике применяются численные методы. В наиболее простом из них, так называемом обратном методе результирующая функция принадлежности рассчитывается путем последовательного применения бинарной алгебраической операции.

Алгоритм нахождения функции принадлежности µ(z) как результата алгебраической операции над двумя произвольными функциями принадлежности µ(х) и µ(у) обратным численным методом состоит из следующих этапов:

1) Для функций принадлежности
разобьем отрезок на части точками

2) Для каждого r_i из решения уравнений µ(х)= r_i и µ(у)= r_i, определяем соответствующие r_i -уровневые множества:

3) Находим r_i -уровневые множества результирующей функции

где * - соответствующая интервальная операция.

Особенности применяемого численного метода позволяют работать с функциями любого вида. На основе данного алгоритма рассчитаны r-уровневые множества для функции .

При подсчете запасов железной руды формируется многоуровневое описание геологических объектов. Можно выделить подсчет запасов по средним значениям, двухмерные и трехмерные геологические модели. Если эти модели и соответствующие понятия создаются на единой информационной базе, то имеется реальная возможность согласования исходных понятий и решений, и уменьшения уровня неопределенности в системе.

Более детальным является подсчет запасов по пластам, блокам и разрезам [4,5]. В этом случае параметры моделей связаны определенными соотношениями: для параметров к_п и к_р идет взвешивание по площадям соответствующих пластов, разрезов; толщины продуктивных пластов суммируются, а запасы в целом по месторождению определяются суммой запасов по пластам, блокам и разрезам.

Следующим уровнем детализации являются двухмерные геологические модели. В этом случае для связи параметров моделей требуется усреднение сеточной области параметров к_п и к_р. В случае трехмерной модели параметры к_п и к_р усредняются. В целом получается многоуровневая система вложенных понятий и моделей.

При описании всех исходных и результирующих параметров с помощью теории нечетких множеств появляется возможность согласования используемых нечетких величин и коррекции по уровням описания в соответствии с предложенной процедурой для многоуровневых иерархических систем.

Литература:

1. Бусленко Н.П. Моделирование сложных систем.- Главная редакция физико-математической литературы изд-ва «Наука». - М.: 1968.- 356 стр.

2. Колесов Ю.Б., Сениченков Ю.Б. Моделирование систем. Динамические и гибридные системы. - СПб.: BHV-Санкт-Петербург. - 432 с.

3. Морозов С.А., Манжула В.Г., Федосеев СВ. Принципы построения математических моделей сложных систем в условиях неопределенности // Фундаментальные исследования. – 2009. – № 4 – С. 74-75.

4. Нормы технологического проектирования горнодобывающих предприятий горной металлургии с открытым способом разработки. – Л.: Гипроруда, 1986. – 264 с.

5. Открытые горные работы: справочник / К.Н. Трубецкой [ и др.]. – М.: Горное бюро, 1994. – 590 с.