Таттибеков К.С.
Таразский государственный педагогический институт, Казахстан
Компьютерное моделирование магнетиков с деформируемой решеткой
Для численного
решения нелинейных уравнений математической физики широко используется конечно-разностные методы. Суть данного
метода заключается в том, что область непрерывного
изменения аргумента х заменяется
конечно-разностной сеткой, а дифференциальные операторы, определяющие уравнения
- разностными соотношениями. При этом решение дифференциальной задачи сводится к
решению системы разностных равнений.
Для
изучения динамики нелинейных волн и солитонов в магнитоупорядоченных
кристаллах часто используют макроскопическое описание магнетиков на основе
уравнения Лаңдау-Лифщица (ЛЛ) [1]:
![]()
где ![]() - означает векторное
произведение в
- означает векторное
произведение в ![]()
При температурах отличных от нуля, атомы
ферромагнетика не являются неподвижными, а совершают малые колебания около
положений равновесия - узлов кристаллической решетки. Из за этого меняется
энергия обменного взаимодействия и возникают взаимодействия между спиновыми
волнами и колебаниями решетки(фононами). Поэтому актуален вопрос о
математическом исследовании моделей соответствующих
ферромагнетикам с деформируемой решеткой.
В этой работе проведена численная
реализация задачи Коши для системы нелинейных эволюционных уравнений,
предложенной в работах [2], описывающая магнон-фононные взаимодействия в 1Д
магнетиках:
![]()
![]()
где 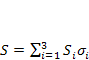 ,
, ![]() - матрицы Паули,
- матрицы Паули,
![]() - неизвестные функции, индексы
- неизвестные функции, индексы ![]() означают соответствующие частные производные по этим переменным,
означают соответствующие частные производные по этим переменным, ![]() - посстоянные действительные числа (параметры уравнений), [, ]-
коммутатор, {,} - антикоммутатор.
- посстоянные действительные числа (параметры уравнений), [, ]-
коммутатор, {,} - антикоммутатор.
Неизвестная матрица-функция ![]() должна
удовлетворят условию
должна
удовлетворят условию
![]()
где ![]() - единичная
2x2 матрица, или в "компонентах"
- единичная
2x2 матрица, или в "компонентах"
![]()
Вектор ![]() описывает
классический спин атомов магнетика, скалярная функция
описывает
классический спин атомов магнетика, скалярная функция ![]() характеризирует
деформацию решетки – смещение атома.
характеризирует
деформацию решетки – смещение атома.
Для численного
решения системы уравнений удобно перейти от спинового вектора ![]() к функциям
к функциям ![]() с помощью формул:
с помощью формул:
![]()
которые согласуются с условием ![]()
Тогда, система перепишется
в виде
![]() (1a)
(1a)
![]() (1б)
(1б)
![]() (1в)
(1в)
В дальнейшем нас будут интересовать
эволюция движения волн на оси х,
имеющие локальные изменения в начальный момент времени, т.е. для уравнений (1)
рассмотрена задача Коши с начальными условиями
![]() (2)
(2)
![]() - известные функции.
- известные функции.
Система
уравнений (1) является квазилинейной. Указать точные решения соответствующей
задачи Коши вида (2) представляется невозможным. Следовательно, для детального изучения решений задачи (1)-(2) необходимо использовать
приближенные методы.
С помощью Фурье
- анализа проводится выбор алгоритма расчета, который является надежным по
устойчивости и эффективным по соображениям численной реализации решений. Исследование устойчивости
проведено в случае модельных уравнений. На основе разработанной методики
проведены численные расчеты и анализ результатов.
Выяснения
вопросов устойчивости решения используемых в дальнейшем разностных схем для
нелинейных уравнений (1) в общем случае является затруднительным. Поэтому для
получения практических рекомендации выбора шагов сетки ![]() ограничимся исследованием
устойчивости разностных схем для следующих уравнений, соответствующие линейной
части системы (1а), (1б)
ограничимся исследованием
устойчивости разностных схем для следующих уравнений, соответствующие линейной
части системы (1а), (1б)
![]() (3)
(3)
Для системы (3) рассмотрим
разностные схемы вида
![]()
![]() (4)
(4)
где ![]() - разностный оператор второй производной,
- разностный оператор второй производной,
![]() - некоторый вещественный
параметр.
- некоторый вещественный
параметр.
Легко показать,
что разностная схема (4)
аппроксимирует систему уравнений (3) с порядком ![]() имеет первый порядок аппроксимации по
имеет первый порядок аппроксимации по ![]() - второй.
- второй.
Исследование
устойчивости разностной схемы (4) проведем методом Фурье согласно критерию
фон-Неймана [3]. В этом случае для множителей перехода гармоник получим
следующее дисперсионное соотношение
![]() =0
=0
где ![]() - соответствующий номер гармоники. Отсюда имеем, что
- соответствующий номер гармоники. Отсюда имеем, что
![]()
Cледовательно, множители перехода гармоник от одного
временного cлоя к другому временному слою удовлетворяют соотношению
![]()
Отсюда видим, что, если ![]() т.е.согласно критерия фон-Неймана
разностная схема устойчива в норме пространства
т.е.согласно критерия фон-Неймана
разностная схема устойчива в норме пространства ![]() по начальным данным. Заметим, что явная разностная схема, соответствующая при
по начальным данным. Заметим, что явная разностная схема, соответствующая при ![]() является абсолютно
неустойчивой.
является абсолютно
неустойчивой.
Руководствуясь
вышеуказанными соображениями, будем рассматривать схему вида (4) ![]() Тогда соответствующие разностные выражения
для уравнений (1а), (1б) будут иметь
вид
Тогда соответствующие разностные выражения
для уравнений (1а), (1б) будут иметь
вид
![]() (5)
(5)
где функции ![]() соответствуют правым частям
выражений (1а), (1б) соответственно,
вычисленные в узлах сетки в момент времени
соответствуют правым частям
выражений (1а), (1б) соответственно,
вычисленные в узлах сетки в момент времени ![]()
Для
аппроксимации уравнения смещения (1в) использовано соотношение
![]() (6)
(6)
где ![]() - некоторый вещественный
параметр.
- некоторый вещественный
параметр.
Разностная
схема (6) при ![]() соответствует схеме
Лакса-Вендроффа, аппроксимирующая уравнение смещения с порядком
соответствует схеме
Лакса-Вендроффа, аппроксимирующая уравнение смещения с порядком ![]()
Основные
расчеты были проведены по разностной схеме (5), (6) при сравнительно малых значении ![]() Сходимость численного решения
проверялась по последовательности сеток с числом узлов
Сходимость численного решения
проверялась по последовательности сеток с числом узлов ![]() при различных
при различных ![]() Сходимость в норме пространства
Сходимость в норме пространства ![]() удовлетворительная. В худщем
случае, когда
удовлетворительная. В худщем
случае, когда ![]() относительная погрешность составляла
относительная погрешность составляла
![]()
Литература
1.Косевич A.M.,Иванов
Б.А., Ковалев А.С. Нелинейные волны намагниченности. Динамические и
топологические солитоны. -Киев:Наукова думка, 1983. -192с.
2.Мырзакулов Р. Новые
солитонные модели 1D магнетиков с деформируемой решеткой /Изв.АНКаз ССР, сер.
физ.-мат., 1989, №6, с. 7-10.
3.Ковеня В.М., Яненко
Н.Н. Метод расщепления в задачах газовой динамики.-Новосибирск:Наука,
1981. -304с.