Detonation characteristics of low-density emulsion explosives sensitized with polystyrene Foam beads, and their applicability in PERIMETER blasting at quarries

S.A. Gorinov

Global Mining Explosive-Russia LLC, Moscow

I.Y. Maslov

Global Mining Explosive-Russia LLC, Moscow

ABSTRACT: It was demonstrated that stable propagation of explosive process is possible in low-density emulsion explosives obtained through mixing of emulsion with a significant amount of polystyrene foam (or other similar) beads. Such process takes place in the form of a detonation-like wave of emulsion drops combustion in explosive gas streams flowing out of the high-pressure area of the reaction zone.

Chemical reaction in such EEs (emulsion explosives) takes places takes place in the form of surface combustion of emulsion particles interacting with the gas stream.

A method was developed for determining parameters of decomposition of low-density EEs, and it was demonstrated that gradual pressure increase takes place in products of explosive’s decomposition during explosion of such EEs.

Analytical criteria were obtained for evaluation of propagation stability of this process.

These findings allow obtaining practically useful results for validation of gentle blasting technology with the use of low-density EEs.

1. TIMELINESS OF THE STUDY

The use of low-density emulsion explosives sensitized with porous beads of materials having acoustic stiffness close to the acoustic stiffness of emulsion (e.g. polystyrene foam beads) may become one of the promising directions for highly mechanized gentle blasting operations in open cast mining. Such EEs are not much exposed to shrinkage under hydrostatic pressure (within the range of charge height of 30-40 meters) [1]. Low densities of such explosives allow for the efficient use of continuous explosive columns in gentle blasting [2], which in turn provides a high degree of mechanization of charging operations.

Previous studies [1,3] have shown that in case the densities of the examined EEs are higher than 0.75 g/cm³ (for EEs with ammonium nitrate oxidation phase), initiation of explosives takes place due to heating of the matrix emulsion matter during its inflow into surface pores of polystyrene foam beads under the pressure in detonation front.

In case the densities of the EEs sensitized with polystyrene foam beads are less than 0.75 g/cm³ (for EEs with ammonium nitrate oxidation phase), deviations were noticed between calculated and experimental values of velocity of detonation (VOD) [1].

In order to explain the deviations between the calculated value and the experimental value of VOD at the density of the polystyrene foam sensitized emulsion explosive less than 0.75 g/cm³ (for EEs with ammonium nitrate oxidation phase), the following hypothesis was suggested:

a) in case the EE under study has low density, a connected “polystyrene foam beads – air pores” system appears within the EE;

b) presence of end-to-end channels changes the EE’s initiation mechanism. In this case, initiation will take place according to the mechanism described in study [4] – under the action of high-enthalpy gas stream filtering from the area of high pressure. At that, chemical reaction takes place in the form of surface combustion of explosive particles interacting with the gas stream.

2. STUDY MATERIALS AND RESULTS

In order to validate these provisions, experimental and theoretical researches were performed.

As a part of field research, experiments were carried out on measuring completeness and velocity of detonation in the process of blasting of open cylindrical charges of the examined EE in cardboard tubes (shells). Shells were made of 1mm thick sheets of laminated electrical cardboard, which were winded in three laps onto the previously prepared cylindrical templates. VOD Mate (Instantel) and HandyTrap (MREL) hardware continuously measuring the resistance value of the conducting sensor’s electrical circuit was used for measuring VOD. Conducting sensor was glued onto to the cardboard sheet before winding onto the template. After winding onto the template, cardboard sheets were fixed with a scotch tape. After template extraction, one of the ends of the resulting tube was filled with Markoflex polyurethane foam, and after that the shell took its final form (the “plug” of the solidified PU foam was preventing the Emulpor from flowing out of the shell; a shell like this can be easily moved across the field). The shell’s length was not less than 1000 mm, the length of the chargeable (with EE) part of the shell – not less than 900 mm.

Let’s take an in-depth look at one of the series of experiments.

The emulsion of the following chemical composition was used to create the EE: NH₄NO₃ – 75.0% of the total mass, H₂O - 18% of the total mass, emulsifier – 1.0% of the total mass, machine oil – 6.0% of the total mass. The emulsion's density at this chemical composition was 1328 kg/m³ (based on laboratory measurements).

In order to sensitize the above-mentioned emulsion, popcorn beads of 40 kg/m³ bulk density and 8.0mm average diameter were used (these beads have porosity and mechanical characteristics that are close to such of the polystyrene foam of similar bulk density). The EE was prepared by mixing of emulsion (EM) with popcorn beads (PPC) at volume ratio: 7 EM and 4 PPC. Mixture density was 600 kg/m³.

Let’s introduce some designations:

ψ - ratio of the bulk volume of popcorn beads to the volume of matrix emulsion;

ρ₀₀ - density of the EE sensitized with popcorn beads;

ρ_em - matrix emulsion density;

ρ_ppc - bulk density of popcorn beads.

In the case under study, ψ =1.75; ρ₀₀ = 600 kg/m³; ρ_em = 1328 kg/m³; ρ_ppc = 40 kg/m³.

According to [5], if condition (1) is true, then a connected “sen›sitizing beads – air pores” system appears within the EE, and the explosive under study has “foggy” structure consisting of matrix emulsion drops, which are separated from each other by air pockets and (or) light, fragile beads.

Packing factor of popcorn beads was defined through laboratory research and amounted to k_pack = 1.6.

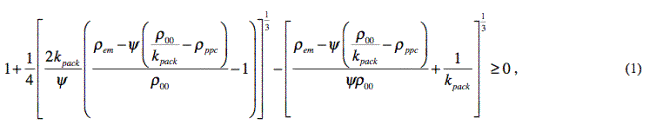
After inserting the given parameter values in (1), we get 0.089 > 0.

Thus, the EE in the series of experiments under study had “foggy” structure consisting of matrix emulsion drops separated from each other by air pockets and (or) light, fragile beads of the material having acoustic stiffness close to the acoustic stiffness of the matrix emulsion.

The external appearance of experimental charge in a cardboard shell of 130 mm diameter is shown in Figure 1.

As the result of experiments, it was determined that when the composition is initiated by boosters made of T-1000-L-PO trinitrotoluene blocks, it detonates completely. At that, VOD amounts to 4123 m/s when blasting 240 mm diameter charge (Figure 2), and to 4065 m/s when charge diameter is 130 mm (Figure 3).

Figure 1. External appearance of experimental charge in a cardboard shell of 130 mm diameter

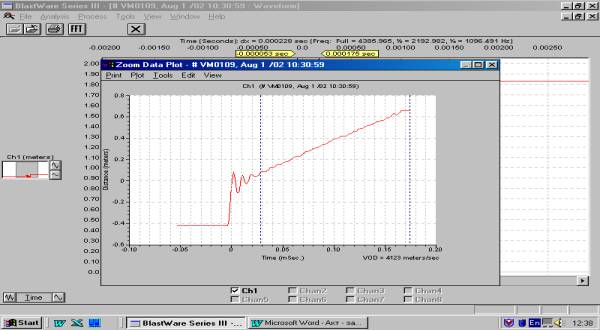
Figure 2. Time variation of the distance covered by the detonation wave

Charge diameter – 240 mm. VOD = 4123 m/s. Booster – T-1000-L-P block

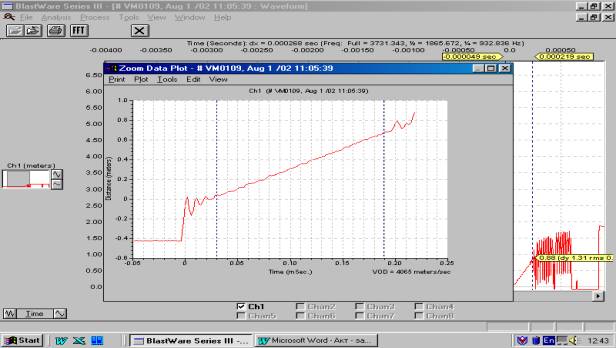
Figure 3. Time variation of the distance covered by the detonation wave

Charge diameter – 130 mm. VOD = 4065 m/s. Booster –T-1000-L-P block

3. DISCUSSION OF EXPERIMENTAL DATA

Let us assume that detonation processes are described by a model that was offered in studies [6-9] for description of detonation of industrial ammonium nitrate explosives. Such model was chosen because it considers the fact that no instant decomposition of explosive takes place during propagation of detonation wave within the above-specified explosives. During the initial period, compression of the explosive takes place under the action of detonation wave as a result of pore space filling with the explosive, then the explosive is heated due to internal friction and heat of gases in the pore space, and only then the explosive ignites. At that, the model considers the fact that the medium acquires additional velocity during compression along the direction of the detonation wave propagation, which allows us to explain a number of previously incomprehensible kinematic effects during propagation of detonation in ammonium nitrate explosives [6].

Within the scope of the assumed model for description of detonation process, we have:

according to the energy conservation law, assuming incompressibility of solid reaction products (within the scope of two-polytropic model for description of detonation products expansion):

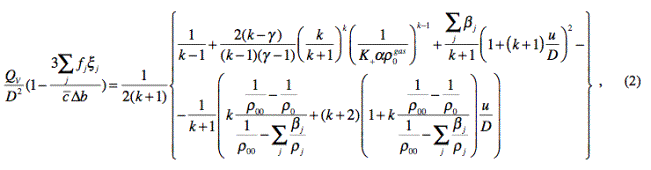
where is the relative molar heat capacity of explosion products;

k is the factor of polytropic curve of explosion products;

γ is the factor of adiabatic curve of explosive gases;

is the total part of solid matter in explosion products;

is the total relative volume of solid explosion products;

ρ₀^gas is the density of gaseous explosion products at the beginning of EE decomposition;

K₊ is a parameter representing the volume of gaseous explosion products in the conjunction point in case of two-polytropic description P=P(V) of gaseous explosion products (based on processing of empirical data, K₊»4.4 [6]);

u is the velocity increment of moving explosion products in the detonation front;

ρ₀ = k_p ρ₀₀ is the density of the explosive at the beginning of decomposition (k_p is the compression factor of the explosive at the beginning of its decomposition);

Q_v is the specific heat of reaction;

c_v is the specific heat capacity of explosion products;

α is the covolume of explosion products (acc. to Vlasov);

Initial density of gaseous explosion products:

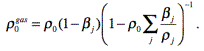(3)

value is determined under the momentum conservation law, and in this case, it approximately equals to: (4)

Explosion gases state equation

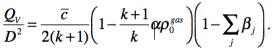(5)

Velocity of detonation(in coordinate system moving along the direction of the process withspeed) equals to:

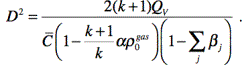(6)

The measured VOD (velocity of detonation in the laboratory system of coordinates) equals to:

(7)

The system of equations (2)-(5) can be solved if the value of compression factor k_p is known.

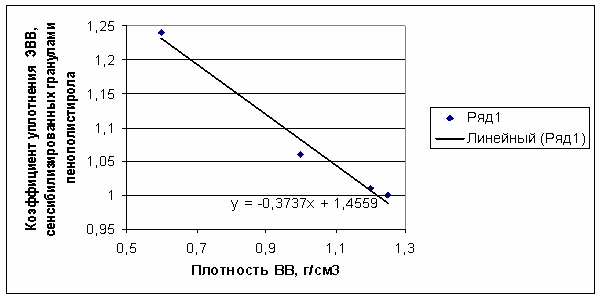
In our case, k_p evaluation was performed through extrapolation of calculated k_p values for the range of Emulpor densities 1.0-1.27 g/cm³ (k_p was calculated by the procedure described in studies [1,3]) to the area of low charge densities. The extrapolation curve is shown in Figure 4. Based on the acquired results, we took

k_p ≈ 1.45 – 0.37ρ₀₀ for evaluative calculations, where ρ₀₀ was taken in g/cm³.

At ρ_ii = 0.6 g/cm³, k_p = 1.23.

The results of VOD calculation through the above-given equations for the series of experiments under study:

= 3195 m/s (D = 2622 m/s; u = 572 m/s).

The calculated value is significantly lower than the experimental value.

Thus, the assumption that detonative decomposition of the EE under study takes place due to the internal friction in the process of pore space filling and due to the heat of gases in the compressing pores doesn’t allow us to explain such high VOD values at such a low EE density.

Hence, another concept is necessary in order to explain the observed VOD values.

In accordance with (1), there is a connected bead-air system in the low-density EE under study. Let us assume that initiation of detonation in this EE will take place in accordance with the explosive initiation mechanism described in study [4].

In this case, initiation of the mentioned EE will take place under the action of high-enthalpy gas stream filtering from the area of high pressure. At that, chemical reaction takes place in the form of surface combustion of explosive particles interacting with the gas stream.

Let’s determine the parameters of the filtering stream of explosive gases from the area of high pressure. Let’s introduce the following designations:

- stream speed with respect to a stationary observer;

ρ_f , T_f - density and temperature of explosive gases in the head end of the stream of explosive gases flowing out from the area of high pressure;

ρ_x , T_x - density and temperature of air in the head end of the air blast wave generated by the stream of explosive gases.

Figure 4. Compression factor of the EE sensitized with polystyrene foam beads as a function of the EE’s density (extrapolation).

In terms of gas dynamic relations [10], within the scope of two-polytropic model of explosive gases expansion, we have the following equations for determination of parameters of the explosive gas stream filtering from the area of high pressure:

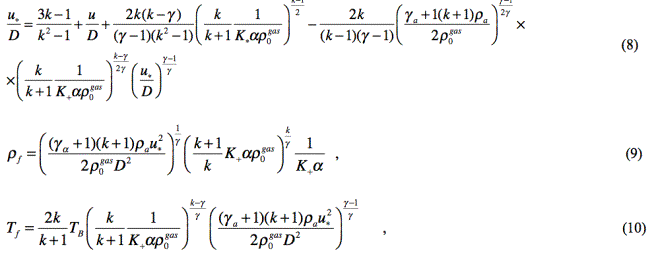
where γ_a =1.2 is the adiabatic exponent of air in the blast wave;

T_B is the temperature of explosion products.

The stream of explosive gases flowing out from the area of high pressure generates a blast wave in the air that is between the beads and inside them (porosity is 95-98%). This blast wave and the following stream of hot explosive gases flow around the drops of matrix emulsion “fog”. If these drops inflame during the period less than the duration of explosion decomposition process in the area of violent chemical reaction (the area of high pressure), then propagation of the explosive process throughout the low-density EE will be determined by the propagation speed of this ignition process.

We shall evaluate the ignition time of emulsion drops according to study [11].

Induction time τ of ignition of an emulsion drop (when it is blown over by the air blast wave and the stream of explosive gases) will be found from the following equations (we assume that due to exceptionally short duration of ignition process, radiant energy plays the leading role in its realization):

(11)

where is the temperature difference; - the “reaction speed – temperature” correlation index; T_H - the initial temperature of emulsion; T_S - the temperature of an emulsion drop’s surface, when it is blown over by the air blast wave and the stream of explosive gases; - activation energy; z - pre-exponential factor; c - specific heat capacity of the matrix emulsion; R - universal gas constant.

We determine the temperature of an emulsion drop’s surface with regard for deceleration of the blast wave and the explosive gas stream, and for thermal activity of substances that take part in heat transfer process [12]:

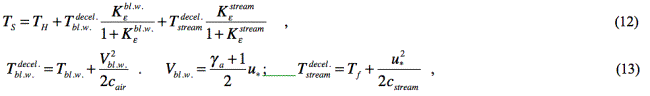
where are factors of thermal activity of (correspondingly) air in the blast wave, and the stream of explosive gases with relation to the emulsion matter:

λ₁ , c_air , ρ_x - heat conductivity factor, heat capacity and density of air (in the blast wave);

λ₂ , c_stream , ρ_f - heat conductivity factor, heat capacity and density of explosive gases in the stream’s head end;

λ_e , c_e , ρ_e - heat conductivity factor, heat capacity and density of the emulsion;

T_bl.w. - temperature of air in the blast wave (it is found from the solutions of [10]).

The condition for occurrence of detonation transmission by the streams of explosive gases flowing out from the area of high pressure will take place in case

τ < t_chem.r. , (14)

where t_chem.r. - duration time of chemical reaction in the area of high pressure.

In the case under consideration

(15)

where R_dr is the average radius of an emulsion drop; v_comb. - the velocity of ablation combustion.

The velocity of ablation combustion is determined with reference to the data from [4]:

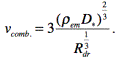(16)

The resulting relations (8)-(10) allow us to evaluate the propagation speed of the detonation-like process, and equations (11)-(16) allow to evaluate the possibility of process transmission by the streams of explosive gases flowing out from the area of high pressure. However, it is necessary to consider the stability of this phenomenon.

According to V.S. Trofimov, detonation process will not be disrupted due to pressure drop in the discharging wave following after the chemical reaction zone if the condition [13] is true:

(17)

ς - the part of the reacted EE matter;

v - specific volume;

- density of explosion products in Chapman-Jouguet point;

θ - the factor of thermal expansion of explosion products in the reaction zone;

Based on transformation of thermodynamic relations [14], it may be shown that

(18)

Let’s substitute (18) into (17) and take integral. As the result, we get the following condition of absence of detonation process disruption:

(19)

In accordance with [15], the state of detonation products in the area of violent chemical reaction approaches to liquid properties. Due to the absence of experimental data for θ, this value has been determined according to the formula [16,17]

(20)

where μ is Poisson ratio (in this case, μ = 0.5); C_sound - sound velocity in explosion products in the reaction zone.

On the basis of (6), (19), (20), we get the following criterion of absence of detonation disruption:

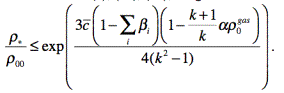(21)

In rough figures, we have the following expressions for some parameters that are included in (21):

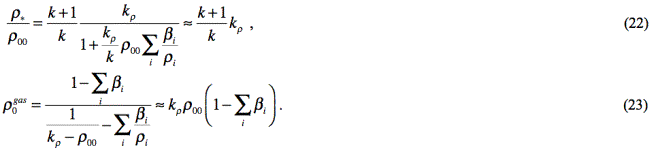
On the basis of (21)-(23), we get the following criterion expression for evaluation of absence of detonation disruption:

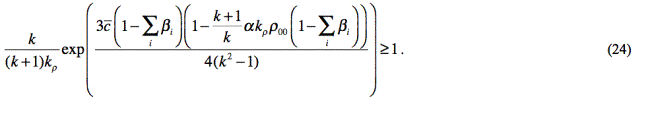
4. RESULTS OF CALCULATIONS USING THE MODEL OF EXPLOSIVE PROCESS STREAM TRANSMISSION

While performing the calculations, we assumed that emulsion ignition starts from exothermic decomposition of ammonium nitrate. Then, the values of activation energy and pre-exponential factor z in formulas (11) may be defined equal to [12]: = 169.5 kJ/mol, z = 6.8 * 10¹³ s^-1. The value of heat capacity of the matrix emulsion was determined in accordance with [18].

Polytropic curve factor – 1.907, adiabatic curve factor – 1.289;

Heat of explosion – 596.5 kcal/kg; specific volume of gases – 1093 l/kg;

Density of explosion gases in the head end of the stream – 0.0457 g/cm³;

Temperature of explosive gases in the head end of the stream – 628 ºK;

Pressure in explosive gases in the head end of the stream – 20.9 MPa;

Pressure in the area of violent chemical reaction – 1.69 GPa

Velocity of the gas stream flowing out from the area of high pressure – 3837 m/s;

Velocity of the air blast wave propagating in front of the stream – 4221 m/s.

Duration time of chemical reaction – 56.2 μs; Induction time of emulsion ignition – 51.7 μs;

Criterion of absence of reaction disruption – 0.982 (~1).

Hence, the idea of the low-density EE initiation by the streams of explosive gases flowing out from the area of high pressure allow us to obtain numerical values of VOD that are close to the experimental values.

5. INDUSTRIAL EXPERIMENTAL TESTING

Industrial-experimental testing of possibility to perform perimeter blasting using a low-density emulsion explosive sensitized with polystyrene foam beads was carried out by OAO “Uralasbest” (OJSC) through industrial-experimental blasting of 141/15-center block [1].

The EE was prepared by mixing-charging machine TSZM-11 (ТСЗМ-11) in the process of hole charging.

During the experiment, 98 dry holes of 115 mm diameter were blasted.

Length of holes – 16.5 m; length of charge – 12.5 m. Charging density – 0.485 g/cm³.

Instantaneous initiation.

Presplitting quality when blasting with low-density EEs is comparable with blasting quality in the process of presplitting with garland charges.

Despite its low density (less than 0.5 g/cm³), the EE has preserved the ability for decomposition.

6. CONCLUSIONS

In low-density EEs sensitized with polystyrene foam (or other similar) beads, it is possible to provide stable propagation of detonation-like wave of emulsion drops combustion in explosive gas streams flowing out of the high-pressure area of the reaction zone.

At that, gradual pressure increase is observed in explosive decomposition products, which is advantageous for performance of gentle blasting.

A method was developed for determining parameters of decomposition of low-density EEs.

Analytical criteria were obtained for evaluation of propagation stability of this process.

The research results allow obtaining useful information for creation of new types of low-density EEs, and validation of gentle blasting technology with the use of such EEs.

ACKNOWLEDGEMENT

Authors express their gratitude for useful discussions of the issues under study to Doctor of Engineering Sciences, Associate Member of the Hungarian Academy of Sciences, V.V. Andreev.

REFERENECES

1. I.Y. Maslov. Increasing the efficiency of blasting preparation of enclosing rocks at Kuzbass open casts with the use of emulsion explosives sensitized with polystyrene foam beads / Ph.D. thesis in Engineering Science, major 25.00.20, M., 2013. – p.132.

2. M.S. Shalaev, G.P. Paramonov. On the question of increasing the efficiency of screening slot by selecting a rational design of perimeter charge. Blasting work No.103/60. M.: Inter-Departmental Commission on Blasting Works at Mining Science Academy, 2010. pp.190-199.

3. S.A. Gorinov, I.Y. Maslov. Evaluation of detonation parameters of emulsion explosives sensitized with plastic polymicrospheres: Individual articles of Mining Research and Information Bulletin (scientific and technical journal). – 2011 – No.7. – pp.53-63. - M.: Publisher “Gornaya Kniga” – 2011

4. V.V. Andreev, A.P. Ershov, L.A. Lukyanchikov. Two-phase low-velocity detonation of porous explosive / Physics of combustion and explosion, 1979, vol.15, No.1, pp.89-93.

5. I.Y. Maslov. Evaluation of characteristic density of emulsion explosives sensitized with polystyrene foam beads / Mining Research and Information Bulletin (scientific and technical journal). – 2014. – No.6.- pp.3-10. .- M.: Publisher “Gornaya Kniga” – 2014г.

6. S.A. Gorinov. Approximating method of detonation parameters calculation for low-density ammonium nitrate explosives // Mining Research and Information Bulletin (scientific and technical journal), 2010, No.10, pp.244-256.

7. Theoretical evaluation of influence of oxidizing agent’s chemical nature on detonation characteristics of emulsion explosives / S.A. Gorinov, V.P. Kuprin, I.L. Kovalenko, E.P. Sobina – In the book: Developing resource saving technologies in blasting works. - Ekaterinburg, pub. Ural Branch of the Russian Academy of Sciences, 2009, pp.191-201.

8. S.A. Gorinov. Theoretical evaluation of detonation parameters of granemites. // Mining Research and Information Bulletin (scientific and technical journal), 2010, No.8, pp.121-130.

9. B.N. Kutuzov, S.A. Gorinov. Physical and technical basics of creation of emulsion-type and granular explosives, and the means for their initiation. // Mining Research and Information Bulletin (scientific and technical journal), 2011, No.7. Preprint. pp.34-52.

10. F.A. Baum, K.P. Stanyukovich, B.I. Shekhter. Physics of explosion.- M.: pub. Fizmatgiz, 1959. p.800.

11. V.N. Vilyunov. Theory of ignition of condensed substances.- Novosibirsk, Science, 1984.- p.189.

12. Theory of combustion and explosion. P.P. Kukin, V.V. Yushin, S.G. Yemelyanov, et. al. – M., pub. Urait, 2014.- p.435.

13. A.N. Dremin. Pulsating detonation front / Physics of combustion and explosion, 1983, No.4, vol.19, pp.159-169.

14. V.G. Levich. Course of theoretical physics. Vol.1.- M.: Science, Chief Editorial Board of Physics and Mathematics Literature, 1969.- p.912.

15. L.D. Landau, K.P. Stanyukovich. On studying detonation of condensed explosives. / Reports of the USSR Academy of Sciences, 1945, т.46, №9, с.399-402.

16. V.N. Belopomestnykh. Acoustic Grüneisen parameter of solid bodies // Letters to Journal of Technical Physics.- 2004.- Vol.30, issue no.3, pp.14-19.

17. E.P. Tesleeva. Research of polymorphic transformations in ion-molecular dielectric materials through methods of physical acoustic and thermal physics // Author’s abstract of the Ph.D. thesis in Physics and Mathematics, Barnaul, 2006.- p.22.

18. S.A. Gorinov, I.Y. Maslov. Thermal-physical properties of non-sensitized emulsion matrix – a component of emulsion explosives // Mining Research and Information Bulletin (scientific and technical journal). Individual articles.- 2011.- No.12, pp.17-20. - М.: pub. “Gornaya Kniga”.