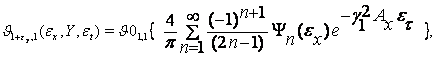18-СИ/ 1. Компьютерная инженерия

 

Швачич Г.Г.

Национальная металлургическая академия Украины,

 г. Днепропетровск, Украина

 ОБ ОДНОМ ПОДХОДЕ К РЕШЕНИЮ  ПРОБЛЕМЫ ЛАТЕНТНОСТИ  ВЫЧИСЛИТЕЛЬНЫХ

КЛАСТЕРОВ MPP АРХИТЕКТУРЫ

 

Актуальность темы исследований

        В настоящее время машинное моделирование является одним из наиболее распространенных и мощных методов исследования сложных систем. При этом нынешний этап научных исследований отличается тем, что имеет место огромная вычислительная мощность современных средств вычислительной техники, при помощи которых проводится соответствующий этап математического моделирования. Однако существует широкий класс задач, решение которых при помощи классического (последовательное) моделирования (особенность его состоит в том, что реализуется на однопроцессорном компьютере) занимает неприемлемо долгое время (недели и месяцы). К таким задачам относятся, например, численное моделирование процессов гидродинамики и металлургической теплофизики [1,2], задачи распознавания образов, оптимизационные задачи с большим числом параметров и т.д. Время решения подобных задач можно существенно сократить, если для моделирования использовать многопроцессорные ЭВМ.

        Проблемы, возникающие при разработке параллельных вычислительных систем  как правило, являются первостепенными и требуют глубокого изучения и исследования.  Действительно, распределенное (параллельное) компьютерное моделирование охватывает весь спектр современной вычислительной техники: суперкомпьютеры, кластерные вычислительные системы, локальные и глобальные сети. Кроме того, распределенное моделирование позволяет решать задачи, требующие большого количества процессорного времени, интегрировать математические модели, которые обрабатываются на различных (в том числе и географически отдаленных) вычислительных системах.

        В настоящее время в мире наблюдается стремительный рост числа многопроцессорных вычислительных систем кластерного типа и их суммарной производительности. В этой связи, проблемы конструирования вычислительных кластеров, а также разработки вычислительных алгоритмов для параллельного процессора являются актуальными и первостепенными.

Некоторые аспекты конструирования высокопроизводительных вычислительных систем кластерного типа

        Впервые в классификации вычислительных систем термин «кластер» ввела компания Digital Equipment Corporation (DEC). Определение кластера было сформулировано следующим образом: кластер – это группа вычислительных машин, которые связаны между собой и функционируют, как один узел обработки информации. Существуют и другие определения «кластера» [3,4], которые связаны с особенностями сегодняшнего развития средств информационных технологий, но они носят, скорее всего, производный характер от определения компании DEC. В данной работе, используя термин «кластер», подразумевается как определение компании  DEC, так и определение, сформулированное в [3,4].

         В настоящее время развитие высокопроизводительных вычислительных систем развивается по двум основным направлениям:

        1. Параллельные компьютеры с общей памятью (архитектура SMP).

        Вычислительные кластеры архитектуры SMP – Summetric Microprocessors отличаются тем, что их вся оперативная память разделена несколькими одинаковыми процессорами. Это обстоятельство снимает      проблемы вычислительных кластеров предыдущего класса, но добавляет новые – число процессоров, имеющих доступ к  общей памяти, по техническим причинам нельзя сделать большим, при этом отмечают, что здесь имеет место проблема масштабирования [3,5].

        2. Массивно-параллельные компьютеры с распределенной памятью (архитектура MPP).  Идея построения вычислительных кластеров архитектуры MPP – Massively Parallel Processing состоит в следующем: берутся серийные микропроцессоры, снабженные каждый своей локальной памятью, и связываются быстродействующими каналами связи.

        У такой архитектуры достоинств много: при необходимости можно добавлять процессоры, увеличивая производительность такого кластера; если ограничены финансовые возможности или заранее известна требуемая вычислительная мощность, то легко подбирать требуемую конфигурацию кластера. Однако здесь есть и один существенный недостаток. Дело в том, что межпроцессорное взаимодействие в процессорах такой архитектуры идет намного медленнее, чем происходит локальная обработка данных самими процессорами, т.е. здесь отмечают, что в ряде случаев может возникать проблема так называемой «медленной» памяти. К данному классу можно отнести компьютеры  Intel Paragon, IBM SP1, Parsytec  и др. Заметим, что к этому классу относят и сети компьютеров, которые все чаще рассматривают как недорогую альтернативу крайне дорогих суперкомпьютеров.

    В данной работе освещается один из подходов к решению проблемы латентности для вычислительного кластера MPP архитектуры и особенности его применения для решения широкого класса многомерных нестационарных задач.

Решение проблемы латентности вычислительных

кластеров mpp архитектуры

        Каждый процессор вычислительного кластера MPP архитектуры работает в своем адресном пространстве и никаких общих переменных с другими процессорами не имеет. В тоже время основным способом взаимодействия между процессорами кластера является посылка сообщений при помощи коммуникационной технологии MPI. Такое взаимодействие осуществляется в MPI посредством явной пересылки сообщений. Вполне очевидно, что межпроцессорное взаимодействие идет намного медленнее, чем происходит локальная обработка данных самими процессорами. Например, если на каком-либо процессоре потребовались данные, расположенные в памяти другого процессора, то на передачу этих данных необходимо время, как правило, значительно превосходящее время обращения к своей локальной памяти.

        В [6] предложено несколько способов разрешения проблемы латентности  и тупиковых ситуаций, основанных на применении соответствующим образом процедур (MPI_SEND, MPI_RECV, MPI_IRECV, MPI_SENDRECV и др.) коммуникационной технологии MPI. В данной работе предлагают свой подход к решению проблемы латентности и разрешения тупиковых ситуаций.  Идея такого подхода состоит в решении указанных проблем алгоритмически, принимая во внимание то обстоятельство, что самая благоприятная ситуация возникает в том случае, когда удается распределить процесс вычислений по пользовательской программе  так, что обмены данными между процессорами отсутствуют вовсе. Проиллюстрируем указанный подход для исследуемого класса задач.

        При решении нестационарных задач рассматриваемого класса задач явными или неявными методами почти всегда расчеты ведутся по временным слоям, последовательно слой за слоем. Поэтому счет по времени особенно эффективен на параллельных вычислительных системах  с общей памятью. Как показали исследования, проведенные в [3], возможность реализации алгоритма по макровершинам оказывается реальной и для широкого круга алгоритмов и в нашем случае. В частности, эта возможность широко используется при решении задач линейной алгебры блочными методами [7]. Очевидно, что здесь целесообразно использовать аналитические методы математической физики.   

При этом проиллюстрируем основные алгоритмические идеи   решения проблемы латентности для параллельного процессора MPP архитектуры на фоне решения следующей задачи.   

        Рассмотрим решение краевой задачи Дирихле для одномерного уравнения теплопроводности

(1)

с начальным

(2)

и граничными условиями

.

(3)

В частности, применив к (1) – (3) интегральное преобразование Лапласа получим решение этой задачи в конечном виде

(4)

 где

(5)

        В (4), (5) L – характерный линейный размер неограниченной пластины

( x1=L/2, x2=L=2), а в качестве входных условий (2), (3) было принято

(6)

 Математическая модель (4) допускает неограниченное распараллеливание алгоритма, как по временной переменной  , так и по координате . Действительно, переход  от функции (4) к ее сеточному представлению приводит к задаче отображения  аналитической функции конечной совокупностью чисел. Если можно назначить один процессор на один узел такого расчета, то становится возможным проведение расчетов во всех узлах сеточной области параллельно и одновременно, минуя замену дифференциального оператора разностным. Но самое главное заключается в том, что данные при этом можно распределять так, чтобы не было пересылок вовсе.

Многомерные задачи.

Рассмотрим дифференциальную задачу вида

 

(7)

где А – некоторый оператор по пространственным переменным, например:

(8)

      Тогда  правая часть уравнения (7) принимает вид

(9)

      Уравнение (14), представленное в виде

расщепляется на следующие два

 

(10)

 

(11)

        Заметим,

(12)

что  и дает основание на каждом интервале времени  вместо задачи (7) последовательно решать задачи (11) и (12).

        Для фактического решения уравнений (10) и (11) формально аппроксимируем эти уравнения какими-либо разностными. Тогда возникает разностная схема расщепления, подробно освещенная в [9] и получившая название локально-одномерного расщепления. Как показано выше, если же при решении задач (10), (11) воспользоваться аналитическими методами, то получим аналитическое расщепление. При аналитическом расщеплении возможно решение задачи аналитическими методами, минуя разностные аппроксимации одномерных операторов Лапласа и временных операторов. В отличие от разностных методов расщепления аналитические схемы позволяют сначала по известным значениям

(13)

 вычислить вспомогательные функции (10)  одновременно на пакете временных слоев , а потом из аналитического решения задачи (11) одновременно вычислить  для всех J одновременно, исключая пересылку данных.

        Пример. Проиллюстрируем алгоритм на примере решения задачи о температурном поле для пластины заданного размера ( L=2 ) при , имеющего в стационарном режиме точное аналитическое решение (ф. 6.18, стр. 162, [10]) при следующих граничных условиях первого рода

(14)

где l=1 – характерный линейный параметр.

        Построение алгоритма начнем с решения задачи (11). При этом для такой задачи точное аналитическое решение в поле изображений имеет следующий вид

 

 

(15)

где

 

(16)

        Функция (15) является мероморфной  и ее особыми точками являются:

     1. S=0   -   простой полюс,

     2. 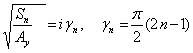 - бесконечное множество простых полюсов, корней уравнения

(17)

Воспользовавшись табличными функциями оригинал изображения (22) представляется тэта-функцией [16]

(18)

где индекс 1 обозначает срединную плоскость по координате .

        Для задачи (10) решение конструируется на основе решения уравнения второго порядка

,

(19)

где:   - известная начальная функция,

         - срединная поверхность области.

        Решение представляется в следующем виде

,

(20)

где:  - частное решение неоднородного уравнения (26),

        C1, D1 – константы интегрирования, определяемые из условий (21)

(21)

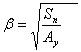- корни характеристического уравнения

.

(22)

        Допустим, что функция  в (19) имеет квадратичную по  зависимость

 ,

(23)

где

 

(24)

центрированные разности первого и второго порядков.

        Легко убедиться, что функция

(25)

удовлетворяет уравнению (19) и, следовательно, является его частным решением. Тогда с учетом (21) найдем

,

 

(26)

так как

        Функция (26) мероморфна и имеет особые точки:

     1. S=0   -   простой полюс,

     2. 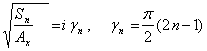 - бесконечное множество простых полюсов, корней уравнения (17).

        Заметим, что второе слагаемое в (26) при S=0 имеет устранимую особую точку. Следовательно, оригиналом изображения  (26) будет следующая тэта-функция

 

(27)

где

 

 

 

 

(28)

        В соответствии с аналитической схемой расщепления сначала по известным начальным условиям (6) вычисляется вспомогательная функция (18). Далее по формуле (27) определяется искомое решение задачи (17)-(19) в разные моменты времени . Результаты моделирования сведены в табл. 1, где сравниваются с точным решением u(1,1/2)=0,8867 в стационарном режиме по изменению установлением температуры в центральном узле.

                                                                                   Табл. 1.

u(1,1/2)

0,985

0,89196

-0,59

1,0

0,88799

-0,13

        Таким образом, при аналитическом расщеплении удается выявить такую информацию о структуре программы, которая задается совокупностью покрывающих функций, аналитических по времени и координатному направлению расщепления. Описание функций в виде самостоятельных программных единиц (процедур, функций), позволяет сократить объем  и улучшить структуру параллельной программы, а также распределить массивы так, что обмены данными между процессорами отсутствуют вовсе.

Выводы

1.  Суперкомпьютеры в настоящее время малодоступны вследствие огромной      

     стоимости и цены обслуживания. В этой связи реальной альтернативой  

     является применение вычислительных систем кластерного типа, один из  

     вариантов, которой  освещается в данной статье.

2. Являясь достаточно новой         технологией,  параллельные вычислительные  

     системы кластерного типа эффективны при решении широкого класса  

     нестационарных многомерных задач, позволяя при этом повысить   

     производительность и качество вычислений.

3.  Предложен эффективный подход к решению проблемы латентности и      

     разрешения тупиковых ситуаций для вычислительных  кластеров     

    архитектуры MPP.

 

ЛИТЕРАТУРА

1.     Роуч П. Вычислительная гидродинамика / Пер. с англ. – М.: Мир, 1980. –

          616с.

2.     Коздоба Л. А. Вычислительная теплофизика. – Киев: Наук. Думка, 1992. –

         224с.

3.     Воеводин В.В., Воеводин В.В. Параллельные вычисления. – СПб.:  

    BHV-Петербург, 2002, 608 с.

4.Иващенко В.П., Швачич Г.Г., Шмукин А.А. Некоторые аспекты              проблемы математического моделирования задач металлургической теплофизики на основе применения  параллельных вычислительных систем кластерного типа // Сучасні проблеми металургії. Наукові праці. Том 7. Дніпропетровськ: «Системні технології», 2005. С. 23-30.

5.     Лацис А.О. Как построить и использовать суперкомпьютер.  – М.: 

    Бестселлер, 2003, 240 с.

6.     Антонов А.С. Параллельное программирование с использованием      

    технологии MPI: Учебное пособие. – М.: Изд.-во МГУ, 2004. – 71 с.

7.Воеводин В.В. Математические основы параллельных вычислений.-         

     М.: МГУ, 1991. – 345 с.

      8. Годунов С.К., Рябенький В.С. Разностные схем ы (введение в       

    теорию). – М.: Наука, 1973. – 400 с.

 9. Самарский А.А. Теория разностных систем. – М.: Наука, 1977.

     – 653 с.

   10. Шнайдер П. Инженерные проблемы теплопроводности. – М.: Мир,        

       1960, 478 с.

    11. Лыков А.В. Теория теплопроводности. – М.: Высшая школа, 1967. –         

       600 с.
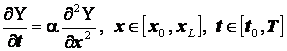
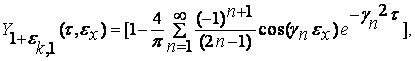
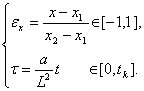
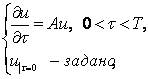
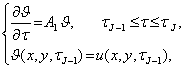
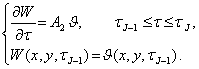
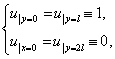
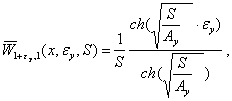
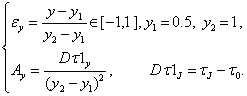
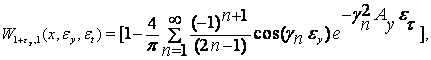
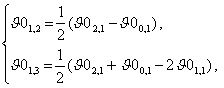
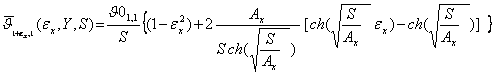