Математика /4. Прикладная математика/

К.т.н. Сластин Ю.В., Федоренко В.Е.

Харьковский национальный технический университет сельского хозяйства

имени П. Василенка

ХНТУСХ

Линейная аппроксимация пространственных кривых,

заданных проекциями на эпюре Монжа.

Решение задачи, рассмотренной в работе [1], начинается с линейной аппроксимации пространственного контура специального вида многоугольником. Для этого, вначале с заданной точностью линейно аппроксимируется одна из монотонных частей его проекции. Вопросу линейной аппроксимации пространственных кривых посвящена настоящая статья.

Пусть пространственная кривая задана двумя проекциями на эпюре Монжа. Уравнения этих проекций и .

Нам нужно аппроксимировать данную пространственную кривую ломаной так, чтобы наибольшее расстояние между ними не превышало заданной величины между ними .

Расстояние между кривой и прямой, параллельной одной из плоскостей проекций, не превышает величины , если расстояние между их проекциями подчинено условию

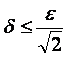. (1)

Действительно, равно длине гипотенузы прямоугольного треугольника, катетами которого являются расстояния проекций такой прямой от проекций кривой. Тогда

,

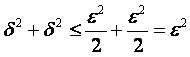т.е. требуемая точность аппроксимации пространственной кривой обеспечивается.

Итак, нам необходимо линейно аппроксимировать проекции кривой с точностью .

Аппроксимацию начнем с точки А₁ проекции кривой на плоскость .

Нам предстоит найти такую хорду, которая отстояла бы от кривой на расстоянии, не превышающем , определив положение второго конца этой хорды.

Определим эту хорду как отрезок прямой, проходящей через точку А₁() под углом к оси:

.

Теперь решение задачи сводится к определению угла при котором наибольшее отклонение хорды от кривой не превышает величины .

Будем рассматривать хорду А₁С₁ как ось новой системы координат с центром в точке А₁. Аппроксимирующая хорда становится параллельной плоскости проекций.

Уравнение кривой в системе координат может быть получено заменой

; . (2)

Пусть теперь уравнение проекции нашей кривой на плоскость имеет вид:

. (3)

Наибольшее отклонение ее от хорды равно экстремуму этой функции в системе координат . Система уравнений для определения угла имеет вид:

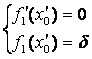(4)

Вторым неизвестным в системе (4) является - абсцисса экстремальной точки.

После определения угла , решив систему уравнений

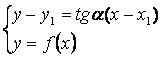, (5)

определим точку С() пересечения найденной хорды с рассматриваемой кривой .

Принимая точку С за начальную, определим тем же способом следующую вершину аппроксимирующей ломаной.

После построения каждого звена ломаной необходимо проверить точность аппроксимации кривой . Для этого, приняв проекцию хорды на плоскость за новую ось абсцисс, и , воспользовавшись преобразованием вида (2), найдем уравнение кривой в системе :

. (6)

При этом

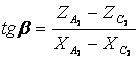. (7)

Теперь нужно произвести исследование функции (7) на экстремум. Если он окажется не более , то пространственная кривая будет аппроксимирована с требуемой точностью.

Если же он окажется больше , то все приведенные выше вычисления нужно повторить, поменяв порядок рассмотрения функций и .

Точность аппроксимации может быть задана не в виде наибольшего допустимого расстояния от хорды до кривой, а в виде наибольшего отклонения значений аппроксимируемой функции и от хорды при одних и тех же значениях (отклонение по вертикали).

Пусть допустимая величина отклонения по оси равна . Это значит, что наибольшее расстояние проекции кривой на плоскости от аппроксимирующей хорды вдоль оси не должно превышать величины .

Итак, через точку А₁ нужно провести хорду так, чтобы удовлетворялась требуемая точность аппроксимации. Для этого нужно найти координаты её вто

рого конца С₁().

Уравнение прямой А₁С₁ запишем в виде

. (8)

Тогда она проходит через точку А₁(). Тогда

Отсюда

и (8) принимает вид

. (9)

Величина отклонения кривой от аппроксимирующей хорды описывается функцией:

. (10)

Решение системы уравнений

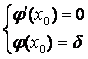(11)

дает угол , обеспечивающий заданную точность.

Координаты точки С₁ определяются из системы уравнений (5).

Теперь нужно проверить точность аппроксимации хордой А₂С₂ кривой .

Уравнение прямой А₂С₂ имеет вид ,

где определяется по формуле (7).

Если экстремум функции

не превышает заданной точности аппроксимации по оси , то задача решена правильно; если же превышает, то все проделанные вычисления нужно повторить, начиная с аппроксимации кривой .

Литература.

1. Сластин Ю.В. Бикубические поверхности на многоугольниках. Сб. трудов МАИ “Кибернетика графики и прикладная геометрия поверхностей”, вып. 331, 1975.