Григорів С.Ф.

Тернопільський національний економічний університет

Івано-Франківський інститут менеджменту, Україна

Математичне моделювання в задачах оцінки зміни заробітної плати та зайнятості

Розглядається модель, в якій взаємодіють роботодавці та наймані робітники, причому вказаний ринок характеризується заробітною платою та числом зайнятих . Вважається що на ньому існує рівновага, тобто [1], виникає ситуація, при якій за плату погоджуються працювати чоловік. Функції та можуть відхилятись від значень і . Вважається, що роботодавці змінюють зарплату пропорційно чисельності зайнятих від значення, що відповідає положенню рівноваги:

Іншим допущенням є гіпотеза про те, що число робітників збільшується або зменшується пропорційно росту або зменшенню заробітної плати відносно рівня в положенні рівноваги:

Для коректної постановки вказаної задачі необхідно задати початкові умови:

Задача – може бути розв’язана за допущенням ; . Очевидно, що записуючи рівняння і у вигляді системи:

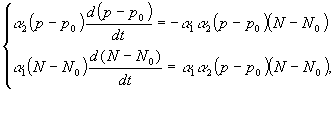
одержуємо:

+=0

Рівність дає можливість детального аналізу ситуації – залежність є рівнянням еліпса, який може бути зображеним у системі координат, центр якої перенесено в точку :

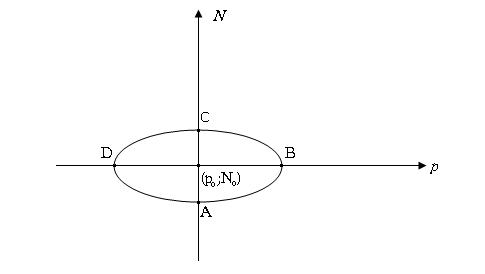
точка А відповідає мінімальній чисельності зайнятих при рівні заробітної плати ; точка В – максимальний рівень заробітної плати при чисельності зайнятих ; точка С – максимальна чисельність зайнятих при , і точка D відповідає мінімальному рівню заробітної плати при .

Крім того, методом виключення змінних система рівнянь – може бути про інтегрована з умовами , при цьому система може бути подана у вигляді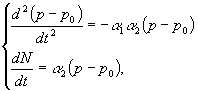

звідки:

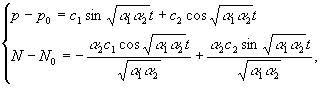
звідси, з урахуванням , одержуємо:

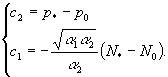
Отже:

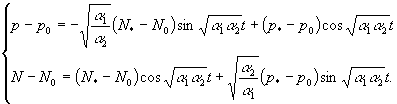
Очевидно, що дозволяє зробити висновок про те, що чисельність зайнятих може бути більша, ніж в положенні рівноваги, як і значення заробітної плати може перевищувати те, яке відповідає значенню рівноваги. Функції є періодичними з періодом . Проводячи оцінку середнього значення заробітної плати та чисельності зайнятих за період коливань за формулою інтегрального середнього :

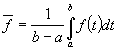
одержуємо:

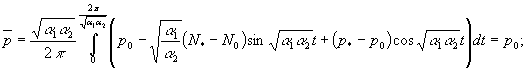
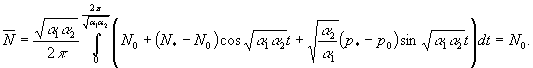
Інтеграли від тригонометричних функцій в та дорівнюють нулю, оскільки відбувається інтегрування по періоду, наприклад:

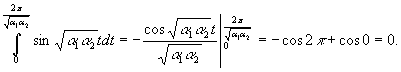
Таким чином можна зробити висновок про те, що середнє значення фонду заробітної плати за період коливань дорівнює значенню в положенні рівноваги . Наведені результати стосуються випадку , , якщо ж розглядати модель і , тобто, більш складний характер залежностей і , то в такому випадку система і допускає або точний аналітичний розв’язок, або для оцінки її поведінки необхідно застосовувати чисельні методи (схеми Рунге-Кутта), що може бути предметом подальших досліджень в даному напрямку: в такому випадку система і набуває вигляду:

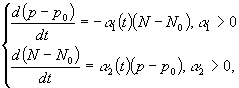
звідки для визначення одержується рівняння:

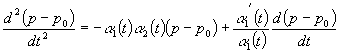
з умовами . При цьому, як було зазначено вище, методика розв’язування визначається складністю аналітичного подання функцій і . Очевидно, якщо і , то співпадає з першим з рівнянь системи , що показує співпадання граничних випадків моделювання вказаної економічної ситуації.

Література.

1. Самарский А.А., Михайлов А.П. Математическое моделирование: Идеи. Методы. Примеры. - / А.А. Самарский, А.П. Михайлов. - М.: ФИЗМАТЛИТ, 2005. - 320с.

2. Зорич В. А. Математический анализ. Часть I. - / В.А. Зорич. - М.: Наука, Гл. ред. физ.-мат. л-ры, 1981. - 544 с.