Климко
О.Г., Вольна М.С.
Полтавський
національний технічний університет
імені
Юрія Кондратюка, Україна
Застосування апарату теорії графів до вдосконалення функціонування
торгівельної мережі
Графи широко використовуються в
різних областях науки і техніки для моделювання симетричних відносин між
об’єктами. Об’єкти відповідають вершинам графа, а ребра − відношенням між
об’єктами. Для різних областей використання, види графів можуть відрізнятися
орієнтованістю, обмеженнями на кількість зв’язків і додатковими даними про
вершини або ребра.
В практичній
діяльності постійно виникають задачі «найкращого» розміщення засобів
обслуговування в мережах або графах. Зокрема, якщо граф зображує мережу доріг і
вершини відповідають окремим районам, то можна взяти задачу оптимального
розміщення лікарень, міліцейських відділів, пожарних відділів, торгівельних
точок і багатьох інших необхідних підприємств та служб. Через значне підвищення
рівня ринкової конкуренції, розміщення торгівельних точок постало одним з
найбільш важливих питань на ринку товарів та послуг, так як саме місцеположення
підприємства відіграє для покупця вирішальну роль у задоволенні потреб
клієнта.
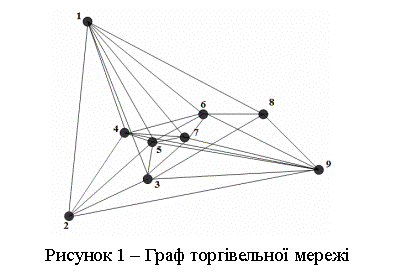
На рисунку 1 зображений граф,
складений на основі існуючої торгівельної мережі. Об’єкти мережі є досить віддаленими
одне від одного та розподілені нерівномірно. Розташовані в місцях масового
скупчення людей: зупинках, ринкових площах та спальних районах.
Малі і середні фірми, що обмежують
збут своєї продукції одним або декількома довколишніми регіонами, мають, як
правило, один склад. Слід мати на увазі, що завдання розміщення і формування
складської мережі – оптимізаційне, оскільки, з одного боку, будівництво нових і
купівля діючих складів і їх експлуатація пов’язані зі значними
капіталовкладеннями, а з іншої – треба забезпечити (разом з підвищенням рівня
обслуговування споживачів) скорочення витрат звернення за рахунок максимального
наближення складів до клієнтів. Тому для даної мережі виконується розміщення 1
складу за мінімальною відстанню від усіх існуючих об’єктів застосувавши
алгоритм Флойда.

Алгоритм даного методу є простим та зручним у застосуванні. Для
знаходження результатів виконуємо наступні дії.
Виділяємо у матриці відстаней ведучий рядок і стовпець. Перевіряємо усі
елементи матриці за допомогою трикутного оператора на можливість їх поліпшення,
та записуємо проміжні пункти у матрицю маршрутів якщо вони є. У результаті
розрахунку отримаємо кінцеву матрицю найкоротших відстаней та матрицю
маршрутів.
У початковій матриці ваг ![]() для всіх
для всіх ![]() і
і ![]() , якщо у графі відсутня дуга
, якщо у графі відсутня дуга ![]() . Покладемо, що
. Покладемо, що ![]() ,
, ![]() . Для усіх
. Для усіх ![]() , таких, що
, таких, що ![]() і для всіх
і для всіх ![]() , таких, що
, таких, що ![]() вводимо операцію
вводимо операцію
![]() . (1)
. (1)
Перевірка на
закінчення
Якщо ![]() , то в графі
, то в графі ![]() існує цикл від’ємної
ваги, що містить вершину
існує цикл від’ємної
ваги, що містить вершину ![]() і розв’язку немає. Закінчення.
і розв’язку немає. Закінчення.
Якщо ![]() і
і ![]() , то отримано розв’язок. Матриця
, то отримано розв’язок. Матриця ![]() дає довжину усіх
найкоротших шляхів. Закінчення.
дає довжину усіх
найкоротших шляхів. Закінчення.
Якщо ![]() , але
, але ![]() , то повернутися до етапу
, то повернутися до етапу ![]() .
.
Самі ж найкоротші шляхи можна знайти за заданими довжинами з допомогою
рекурсивної процедури. При цьому як до повернення до вагової матриці ![]() зберігається та
оновлюється друга
зберігається та
оновлюється друга ![]() матриця
матриця ![]() . Елемент
. Елемент ![]() вказує вершину, що є
попередньою вершині
вказує вершину, що є
попередньою вершині ![]() у найкоротшому шляху від
у найкоротшому шляху від ![]() до
до ![]() .
.
У відповідності з формулою (1) на кроці 3
алгоритм оновлення матриці відбувається таким чином:
![]()
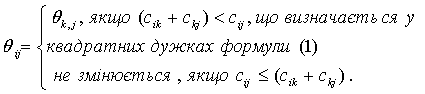 (2)
(2)
У кінці алгоритму найкоротші шляхи отримуємо
безпосередньо із завершальної матриці ![]() . Даний метод можна застосовувати як до невід’ємних так і до
будь-яких вагових матриць.
. Даний метод можна застосовувати як до невід’ємних так і до
будь-яких вагових матриць.
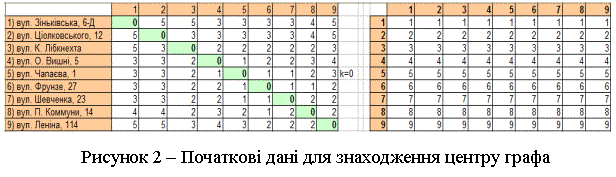

За допомогою трикутного оператора
була здійснена перевірка на поліпшення, і за результатами всі початкові
відстані є мінімальними. Дев’ята ітерація має наступний вигляд (рисунок 3).
Центр графа визначаємо за
допомогою медіани. Медіана графа – така вершина x, сумарна відстань від якої до
всіх інших вершин графа мінімальна. Сумарна відстань від вершини до всіх інших
вершин – СВВ(i) визначається
співвідношенням СВВ(i) = Σсi,j – сумарна відстань від вершини i
до всіх j .
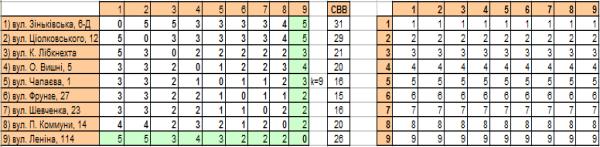
Рисунок 3 – Результати розрахунків

СВВ(x) = min {СВВ(i)} (3)
Зауважимо, що сума значень
елементів i-го рядка матриці СN
відстаней вершин – вершина дорівнює сумі відстаней від вершини до всіх інших
вершин графа, тобто дорівнює СВВ(i).
Отже, медіана відповідає будь-якому рядку матриці СN, для якої сума значень елементів мінімальна. Елементи
матриці СN можуть були
розраховані за допомогою алгоритму Флойда.
Мінімальне значення має СВВ (6) = 15, а це означає, що вершина 6
(вул. Фрунзе, 27) є медіаною графа.
Висновок: Максимальне
наближення складів до споживачів дає можливість чіткіше і точно реагувати на
зміну їх вимог, що дозволяє скоротити витрати від упущених продажів. Розміщення складу в
центрі графа покращить управління всіма торгівельними точками та зменшить
витрати на перевезення. Дана модель враховує зміну середовища, тому при розширенні
чи скороченні мережі підприємства алгоритм можна застосувати знову,
використовуючи нові показники.
Література:
1. Зыков
А. А. Основы теории графов / А.А.Зыков. − М .: «Наука», 1987. − 384
с.
2. Кристофидес
Н. Теория графов. Алгоритмический подход / Н.Кристофидес. − М.: «Мир»,
1978. − 432 c.
3. Богомолов
А.М., Салий В.Н. Алгебраические основы теории дискретных систем /
А.М.Богомолов, В.Н.Салий. − М.: «Физматлит», 1997. − 368 с.