Кулешов К.Ю.

Донской Государственный Технический Университет, Россия

Генетический алгоритм с несколькими ареалами

Существует множество задач оптимизации, для которых специально не разработаны методы. Для них может стать основным методом решения простой перебор. Подобные задачи позиционируют как задачи высокой вычислительной сложности (класс NP и NP-полная задача).

Примеры таких задач: задача о выполнимости булевых формул, задача о независимом множестве, задача о клике, задача о покрытие множества, задача о вершинном покрытии, проблема раскраски графа, проблема Штейнера, задача коммивояжера, кратчайшее решение «пятнашек» размера n x n, и другие специфические задачи n-переменных.

Хорошей альтернативой использования перебора при решении перечисленных задач являются эвристические методы. Как известно, эвристические алгоритмы не имеют строгого математического обоснования, но, тем не менее, дают приемлемые решения задач в большинстве практически значимых случаях. Более того, в действительности может быть даже известно (то есть доказано) то, что эвристический алгоритм формально не верен. При этом его все равно можно применять, если он дает неверный результат только в отдельных, достаточно редких и хорошо выделяемых случаях, или же дает неточный, но все же приемлемый результат.

При использовании эвристических методов важно понимать, что данные алгоритмы имеют следующие особенности: они не гарантируют нахождение лучшего решения; они не гарантируют нахождение решения, даже если оно заведомо существует (возможен «пропуск цели»); они могут дать неверное решение в некоторых случаях.

Пример оценки эвристического решения.

Рассмотрим умозрительный пример. Допустим, что имеется известный, но чрезвычайно сложный точный алгоритм решения задачи, и эвристика, которая требует в 1000 раз меньше затрат и чаще всего даёт приемлемое решение (пусть в 95 % случаев). Для простоты примем, что цена точного решения постоянна, как и цена ошибки.

Тогда в среднем решение эвристическим методом будет стоить , где T — цена точного решения, а E — цена ошибки. Средняя разница в цене решения точным и эвристическим методом , то есть эвристика в среднем оказывается выгоднее точного решения, если только цена ошибки не превышает двадцатикратную (!) цену точного решения.

Если же на выходе результат решения критически оценивается человеком, то ситуация становится ещё лучше: когда ошибка, выданная эвристикой, оказывается достаточно мала, чтобы человек её не заметил, цена этой ошибки обычно гораздо ниже, а серьёзные ошибки будут отсеяны «фильтром здравого смысла», следовательно, не нанесут существенного вреда.

Одним из эвристических алгоритмов является генетический алгоритм (ГА), используемый для решения задач оптимизации и моделирования, путем случайного подбора, комбинирования и вариации искомых параметров с использованием механизмов, напоминающих биологическую эволюцию.

Схематично алгоритм можно представить так:

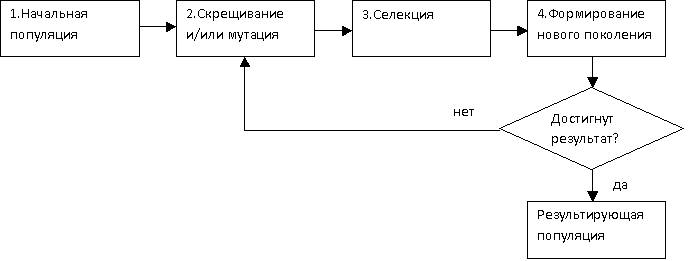
Задача формализуется таким образом, что бы ее решение могло быть закодировано в виде вектора («генотипа») генов, где каждый ген может быть битом, числом или неким другим объектом. В классических реализациях ГА предполагается, что генотип имеет фиксированную длину. Однако существуют вариации ГА, свободные от этого ограничения.

Создание начальной популяции.

Перед первым шагом нужно случайным образом создать начальную популяцию; даже если она окажется совершенно неконкурентоспособной, вероятно, что генетический алгоритм все равно достаточно быстро переведет её в жизнеспособную популяцию. Таким образом, на первом шаге можно особенно не стараться сделать слишком уж приспособленных особей, достаточно, чтобы они соответствовали формату особей популяции, и на них можно было подсчитать функцию приспособленности (Fitness). Итогом первого шага является популяция H, состоящая из N особей.

Размножение (Скрещивание)

Размножение в генетических алгоритмах обычно половое — чтобы произвести потомка, нужны несколько родителей, обычно два.

Размножение в разных алгоритмах определяется по-разному — оно, конечно, зависит от представления данных. Главное требование к размножению — чтобы потомок или потомки имели возможность унаследовать черты обоих родителей, «смешав» их каким-либо способом.

Мутации

К мутациям относится все то же самое, что и к размножению: есть некоторая доля мутантов m, являющаяся параметром генетического алгоритма, и на шаге мутаций нужно выбрать mN особей, а затем изменить их в соответствии с заранее определёнными операциями мутации.

Отбор

На этапе отбора нужно из всей популяции выбрать определённую её долю, которая останется «в живых» на этом этапе эволюции. Есть разные способы проводить отбор. Вероятность выживания особи h должна зависеть от значения функции приспособленности Fitness(h). Сама доля выживших s обычно является параметром генетического алгоритма, и её просто задают заранее. По итогам отбора из N особей популяции H должны остаться sN особей, которые войдут в итоговую популяцию H'. Остальные особи погибают.

Очевидно, что алгоритм во многом зависит от выбора способа скрещивания и мутации. То есть если выбрать не подходящие поставленной задаче способы, задача будет сходится медленнее (если вообще будет сходится). Особенно тяжело подобрать способ для новых задач, с непрогнозируемым поведением.

Решением может стать генетический алгоритм с несколькими ареалами. Так как ГА строится по аналогии с биологическими процессами, то, проследив другие биологические процессы, можно сформировать новый алгоритм. Обратимся к понятию ареал. Популяции одного вида, находясь в различных ареалах обитания, подвержены влиянию различных факторов, свойственных только их ареалам. Этим мы и воспользуемся при создании нового алгоритма.

Рассмотрим абстрактную задачу, для которой мы можем применить ГА. Сформируем N комбинаций способов скрещивания и мутации. Условно, каждая комбинация будет представлять один ареал обитания. Как и в обычном ГА мы будет формировать начальную популяцию. Из нее формируется общая популяция, из которой будут формироваться популяции для каждого ареала. Что б результаты как то объединялись, каждые n итераций будет из всех ареалов выбираться лучшая популяция, из которой будет происходить новое заселение ареалов обитания. Для удобства, назовем n итераций одним жизненным циклом популяции. Проще говоря, каждый жизненный цикл сильнейшая популяция будет заселять все ареалы обитания.

Подобный алгоритм способен показать результат лучше, чем обычный ГА, так как прорабатывает больше возможностей спуска по решению. Однако стоит отметить его недостаток: он более ресурсоемкий по сравнению с ГА. Если заранее известно, что задача требует значительного количества итераций, возможно объединить ГА и ГА с несколькими ареалами. Например так: выбираем число m-жизненных циклов популяции, по истечению которых будет производиться анализ, какой из N ареалов дал больше лучших популяций.

да

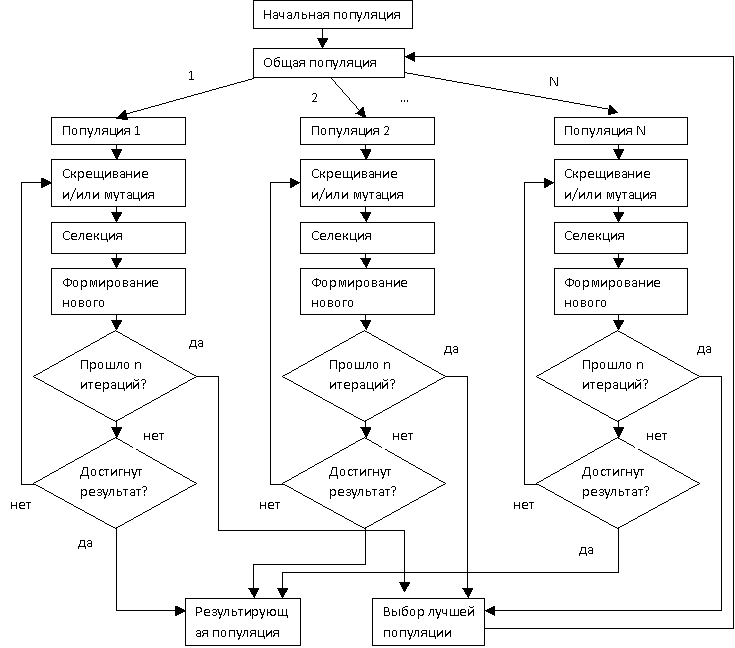
Схема генетического алгоритма с несколькими ареалами.

Если один ареал дал заранее заданный процент лучших популяций (например 95%), то считаем его комбинацию способов скрещивания и мутации лучшим для данной задачи, а все остальные фиктивными. И дальше решение идет по стандартному ГА с данной комбинацией.

Литература:

1. С.Гудман, С.Хидетниеми, Введение в разработку и анализ алгоритмов, М.:"Мир", 1981.

2. Емельянов В. В., Курейчик В. В., Курейчик В. М. Теория и практика эволюционного моделирования. — М: Физматлит, 2003. — С. 432. — ISBN 5-9221-0337-7

3. Гладков Л. А., Курейчик В. В., Курейчик В. М. Генетические алгоритмы: Учебное пособие. — 2-е изд. — М: Физматлит, 2006. — С. 320. — ISBN 5-9221-0510-8

4. Курейчик В. М., Лебедев Б. К., Лебедев О. К. Поисковая адаптация: теория и практика. — М: Физматлит, 2006. — С. 272. — ISBN 5-9221-0749-6