Никишина Н.А.

Лесосибирский педагогический институт – филиал ФГАОУ ВПО

«Сибирский федеральный университет», Россия

Построения одной линейкой на клетчатой бумаге

Теория геометрических построений зародилась в Древней Греции и именно оттуда пришла к нам традиция любое решение задач на построение выполнять циркулем и линейкой. Но впоследствии учеными был поставлен вопрос о том, какие построения возможны с использованием меньшего количества чертежных инструментов, например, одним циркулем или одной линейкой. В 1672 г. Г. Мором, а затем Л. Маскерони в 1797 г. была доказана теорема о том, что любая задача, решаемая циркулем и линейкой, может быть решена одним только циркулем.

При наличии только линейки мы можем решить очень ограниченный круг задач. Например, одной линейкой нельзя проводить параллелей и перпендикуляров, нельзя разделить отрезок пополам. Но конструктивные возможности линейки можно расширить с помощью некоторых дополнительных фигур, таких как: две параллельные прямые, прямая, содержащая равные отрезки, параллелограмм, окружность с отмеченным центром. Каждая из вышеперечисленных фигур по-разному увеличивает конструктивную мощь линейки. Так было доказано, что если на плоскости даны две параллельные прямые, то можно данные отрезки увеличивать в произвольное число раз, делить и проводить другие параллельные прямые [6]. Если даны две параллельные прямые и отрезок, лежащий на одной из них, то можно удвоить этот отрезок. Если в плоскости даны какие-либо две пары параллельных прямых, т.е. некоторый параллелограмм, то можно провести по всем направлениям параллельные прямые, т.е. провести прямые, параллельные данной прямой через данную точку; каждый произвольно данный отрезок взять кратным или разделить в данном отношении [4]. Если на плоскости даны какая-нибудь окружность и её центр, то с помощью одной линейки можно выполнить следующий ряд задач: из любой точки провести прямую, параллельную данной прямой и опустить на данную прямую перпендикуляр; на данной прямой от данной точки отложить отрезок, равный данному отрезку; построить точки пересечения двух окружностей, центры которых — данные точки, а радиусы — данные отрезки [5].

В рамках данной статьи нас интересует вопрос о том, как влияет на конструктивные возможности линейки наличие квадратной сетки, которая есть в любой тетради. Нетрудно заметить, что квадратная сетка задает все перечисленные ранее фигуры вместе, за исключением окружности. Притом выбирать эти фигуры на квадратной сетке мы можем самым различным образом. А если в плоскости дан некоторый квадрат, то можно дополнительно решить следующие задачи: на данную прямую из некоторой данной точки опустить перпендикуляр, данный прямой угол разделить пополам и данный угол увеличить в произвольное число раз. Таким образом, при наличии квадрата на плоскости в общем виде решаются задачи на построение перпендикуляров и параллелей.

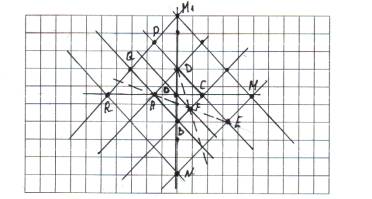
Покажем, что если задан квадрат, то с помощью одной линейки можно построить и квадратную сетку (черт. 1).

Черт. 1

Пусть задан квадрат ABCD. Проведем диагонали АС и ВD, и через точку их пересечения О прямую l, параллельную АВ (черт.2), используя свойства трапеции.

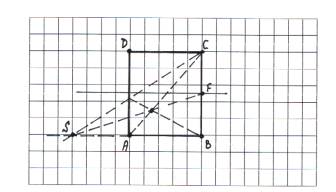
Черт. 2

Пусть ВС∩l=F. Проведя AF найдем точку Е=DC∩AF. Очевидно, что СЕ=DC. Аналогично, DF∩АВ=К и ВК=АВ, а ЕК||AD. Итак, ВСЕК- квадрат, равный данному АВСD. Также получается квадрат AQPD. Точки М и М₁ определят еще три квадрата (выше DC). Аналогично будут построены три квадрата ниже АВ. Так часть плоскости внутри RM₁MN оказалась разграфленной.

Может ли, построенная на базе квадрата квадратная сетка увеличить конструктивные возможности линейки по сравнению с квадратом? Оказывается, нет. По-прежнему мы сможем решать только те задачи, которые принципиально разрешимы линейкой с данным квадратом. То есть квадрат и квадратная сетка теоретически эквивалентны. Но практически решение задач на квадратной сетке, благодаря наличию множества фигур ею задаваемых, значительно упрощается.

Литература:

1. Атанасян, В. А. Задачник-практикум по проективной геометрии [Текст] / В. А. Атанасян, Н. Г. Федин – Просвещение, 1964.

2. Прасолов, В. В. Задачи по планиметрии (изд. пятое) [Текст] / В. В. Прасолов – М: МЦНМО: ОАО «Московские учебники», 2006.

3. Штейнер, Я. Геометрические построения, выполняемые с помощью прямой линии и неподвижного круга [Текст] / Я. Штейнер – М: Государственное учебно-педагогическое издательство наркомпроса РСФСР, 1939.