Математика/5. Математическое моделирование

Аманбаев Т.Р., Аширбаев К.А., Джамиева Б.

Южно-Казахстанский государственный университет им. М. Ауэзова

Моделирование и расчет осаждения дисперсной фазы в суспензии с учетом эффекта стесненности

Процесс осаждения (седиментации) суспензии часто используется в различных отраслях химической технологии (очистка жидкости от твердых примесей, разделение смесей и т.п.) [1,2]. Этот процесс также используют для седиментационного анализа дисперсных систем с целью определения их дисперсного состава. При анализе седиментационных процессов в суспензии обычно рассматривают случай, когда частицы дисперсной фазы движутся независимо друг от друга. Такое свободное осаждение наблюдается только при малых содержаниях твердой фазы в суспензии, когда расстояние между частицами таково, что не происходит ни соударений, ни взаимного влияния частиц. При достаточно высоких содержаниях дисперсной фазы поведение системы кардинально меняется. Однако этот случай в настоящее время исследован не достаточно. В связи с этим изучение влияния стесненности частиц дисперсной фазы на процесс седиментации суспензии становится актуальной. Одним из способов учета взаимодействия дисперсных частиц между собой является введение собственного давления псевдогаза частиц [1]. Данная работа посвящена моделированию процесса стесненного осаждения дисперсных частиц в суспензии с учетом давления “псевдогаза” частиц, появляющегося за счет их столкновений между собой. Будем считать, что перенос частиц под действием силы тяжести доминирует над диффузионным потоком, направленным в противоположную сторону. Рассмотрим процесс седиментации в полубесконечном контейнере, ограниченном снизу и содержащем однородную двухфазную суспензию несжимаемой жидкости с твердыми сферическими частицами. Задачу рассмотрим в одномерной постановке и в предположении, что силами инерции из-за ускорений фаз и их сжимаемостями можно пренебречь. Такие движения реализуются при малых, по сравнению со скоростями звука в фазах, скоростях течений и отсутствии резких изменений параметров потока. При достаточно большом содержании частиц в суспензии необходимо учитывать эффект столкновений частиц между собой, который приводит к появлению переноса импульса в дисперсной фазе. Действительно, уже при объемных содержаниях дисперсной фазы ≥0.1 расстояния между поверхностями частиц или размеры проходов между частицами становятся меньше их диаметра, и частица не может свободно проскакивать между двумя другими [1]. Кроме того, столкновения частиц в смеси может происходить также в том случае, когда дисперсная фаза состоит из полидисперсных частиц или частиц разных плотностей, так как частицы разных размеров или плотностей при осаждении двигаются с разными скоростями. В связи с этим следует ввести тензор напряжений дисперсной фазы . С учетом этого обстоятельства систему уравнений одномерного безынерционного движения двухфазной смеси можно записать в виде (ось z направлена вверх против силы тяжести)

, , (1)

, (2)

, , , , , =const

Здесь и далее нижние индексы 1 и 2 соответствуют несущей и дисперсной фазам; - скорости, объемные содержания, истинные и приведенные плотности фаз (i=1,2); - давление в несущей среде; g - ускорение силы тяжести; d – диаметр частиц; динамическая вязкость жидкости; ψ – коэффициент, учитывающий влияние объемного содержания дисперсных частиц на силу, приходящуюся на одну частицу (или коэффициент, учитывающий стесненность осаждения) и зависящий от структуры расположения частиц; - тензор напряжений псевдогаза частиц, появляющийся за счет соударений частиц между собой; t - время; z - вертикальная координата. Уравнения (1) это уравнения неразрывности несущей и дисперсной фаз, уравнения (2) – уравнения сохранения импульсов фаз. Сила межфазного взаимодействия задана, как в монодисперсной смеси в квазистационарном приближении в соответствии с законом Стокса с учетом стесненности частиц, задаваемой коэффициентом ψ. Для коэффициента стесненности частиц, исходя из различных схем расположения частиц дисперсной фазы, получены разные формулы [1]. В частности, схема ползущего течения вокруг хаотически расположенных частиц приводит к формуле [3,4]

, (3)

Для тензора напряжений дисперсной фазы в [1] предложено следующее выражение

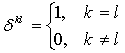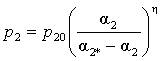, ; , (4)

(, <)

где - критическое объемное содержание частиц, соответствующее плотной упаковке. В случае, когда частицы соприкасаются друг с другом, а их центры образуют кубическую решетку , а при наиболее плотной упаковке, когда центры частиц образуют тетраэдрическую решетку . Из (4) видно, что при давление стремится к бесконечности. Однако в реальных смесях редко достигает значения, соответствующего плотной упаковке. Поэтому можно предположить, что для реальных суспензий ≤<. Согласно опытным данным в свободной засыпке случайного характера [5]. Следует отметить, что для давления псевдогаза частиц кроме (4) существуют и другие выражения, предложенные, например, в [5-7]. Как отмечено в [1], при 0<η<2 система уравнений (1), (2) становится гиперболической, а ее решения устойчивыми при и . При этом существует такое , что при данная система гиперболична, а ее решения устойчивы при любых значениях . Отметим, что уравнение состояния дисперсной фазы (4) при η=1 соответствует среде Ван-дер-Ваальса с постоянной температурой без учета силы отталкивания.

Система (1), (2) с учетом замыкающих соотношений (3), (4) представляет собой замкнутую систему относительно искомых скоростей и объемных концентраций фаз и при заданных свойствах дисперсной системы (вязкости несущей среды, истинных плотностей фаз и диаметра частиц) описывает ее поведение в одномерной постановке.

Литература:

1. Нигматулин Р.И. Динамика многофазных сред. - М.: Наука, 1987.

2. Ровинский Л.А. Седиментация суспензий. М.: Компания Спутник+, 2003.

3. Batchelor G.K. Sedimentation in a dilute dispersion of spheres // J. Fluid Mech. – 1972.

4. Головин А.М., Чижов В.Е. К расчету скорости осаждения однородной суспензии // ПММ. – 1978. – Т.42, №1. – С. 105-113.

5. Гольдштик М.А. Элементарная теория кипящего слоя. // ПМТФ. 1972. №6. С. 106-112;

6. Буевич Ю.А. Гидродинамическая модель дисперсного потока // Изв. РАН. МЖГ. 1994. №1. С. 79-87.

7. Berres S., Burger R., Tory E.M. Applications of polydisperse sedimentation models// Chemical Engineering Journal. 2005. 111. pp. 105-117.