Технические науки/10.Горное дело

К.т.н. Каражанов А.А., профессор Адырбеков М.А.

Таразский государственный университет имени М.Х.Дулати,

Республика Казахстан

КОНСТРУИРОВАНИЕ КАНАЛОВЫХ поверхностЕЙ туннелей С ИСПОЛЬЗОВАНИЕМ ПРЕОБРАЗОВАНИЯ Д₂

Целью данной статьи является разработка теории (2-2)-значного преобразования Д₂ с вертикальной осью симметрии, порождаемого отображением на плоскость двуполостного гиперболоида.

(2-2)-значное преобразование Д₂ определяется по нижеприведенному уравнению:

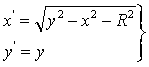, (1)

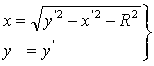. (2)

Графическая модель геометрического преобразования Д₂ примет следующий вид:

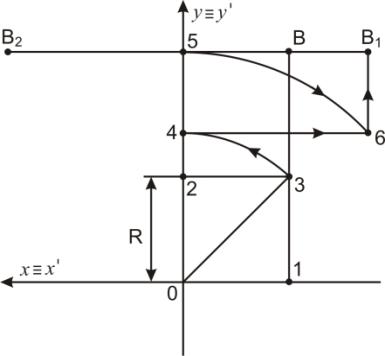
Рисунок 8 – Построение графической модели преобразования Д₂

Далее рассмотрим формообразование кривых 4-го порядка с применением преобразования Д₂, когда прообразом представляют собой окружность, который на плоскости имеет различные расположения.

Преобразование окружности

В общем случае каждая точка окружности m преобразуется в четыре точки плоскости. Множесто точек окружности m отображается в кривую 4-го порядка m^' с использованием преобразования Д₂. Уравнение кривой m^' определяется следующим образом:

1) уравнение прообраза m запишем в виде:

, (3)

где х, у – координаты точек прообраза;

с, d, r – постоянные коэффициенты.

Значения х и у из системы уравнении 1 подставив в уравнение 3, получим уравнение кривой m^' в виде:

, (4)

где х^' и у^' – координаты точек образа;

с, d, r – постоянные прообраза;

R – параметр преобразования Д₂.

Ниже приведены примеры отображения окружности и эллипса в кривую 4-го порядка с применением преобразования Д₂.

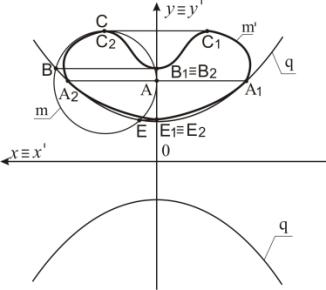
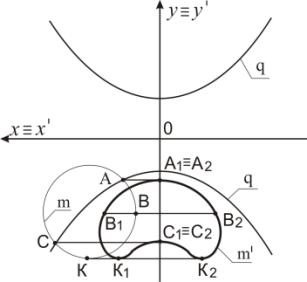
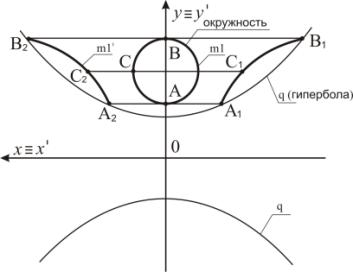
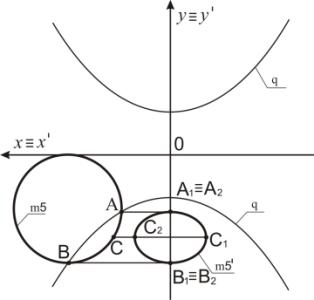
Рисунок 2 – Преобразование окружности

Рассмотренные примеры показывает характер изменения формы образа (кривой 4-го порядка), когда прообраз занимает различные положения на плоскости. Выявленные свойства геометрических преобразований Д₂ позволяют их использовать в решении прикладных задач начертательной геометрии. Получены новые кривые 4-го порядка с использованием (2–2)-значного преобразования Д₂, которые могут быть использованы в конструировании каналовых поверхностей туннелей.

Литература

1. Джапаридзе И.С. Геометрические преобразования пространства и их применения в начертательной геометрии. Методы начертательной геометрии и ее приложения. – М.:1955 – 54-222 с.

2. Ермаков А.В. Кремоновы преобразования пространства в конструировании рациональных каркасных поверхностей: автореф. ...канд.техн.наук: 05.01.01. – М.: МТИПП, 1977 – 17 с.

3. Завьялов Ю.С.,Леус В.А., Скороспелов В.А. Сплайны в инженерной геометрии. - М.: Машиностроение, 1985 – 222 с.

4. Конакбаев К.К. Конструирование обводов из дуг уникурсальных циркулярных кривых посредством кремоновых инволюций. автореф. ...канд.техн.наук: 05.150. – М.: МТИПП, 1972 – 18 с.

5. Котов И.И. Алгоритмы конструирования каркасных поверхностей. – М.: МАИ, 1975.