Современные информационные технологии/

2. Вычислительная техника и программирование

Д.т.н. Ромм Я.Е., к.т.н. Забеглов В.В.

Таганрогский государственный педагогический институт

им. А.П. Чехова, Россия

ТАНТК им. Г.М. Бериева, Россия

Алгоритм пилообразного преобразования В параллельной форме

с переменым числом отсчётов

Введение. Ортогональные преобразования (ОП) используются для обработки сигналов, представляющих различную информацию, такую, как сейсмические и акустические данные, данные биологических и биомедицинских исследований, информацию в области обработки изображений и речевых сигналов, в области отбора признаков при распознании образов, анализа и проектирования систем связи. Среди ОП активно применяется пилообразное преобразование, которое эффективно используется для обработки изображений, например, для представления постепенного изменения яркости вдоль строки изображения, обеспечивает высокую степень концентрации энергии изображения [4]. При использовании ОП возникают задачи повышения скорости и сокращения объёма вычислений. В работе предлагается решение задачи быстродействия посредством видоизменения алгоритма пилообразного преобразования, включающего построение матрицы ОП, к параллельной форме. Параллельное построение матрицы для переменного числа отсчетов дает возможность производить преобразование с наперёд заданной точностью. Параллельные алгоритмы рассматриваются на модели неветвящихся параллельных программ [1,2] без учета обмена.

ОП записываются с помощью матричных обозначений

, (1)

– вектор-столбец входных данных длиною , – матрица ОП размером , – вектор-столбец коэффициентов преобразования длиною , – степень двойки.

Матрица пилообразного преобразования задаётся рекуррентной формулой [3]

,

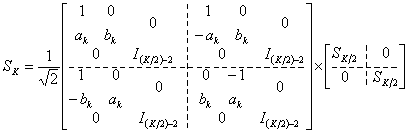, , (2)

где – единичная матрица -го порядка. Постоянные и , вычисляются по формулам [4]:

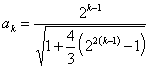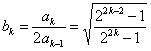, , (3)

Алгоритм строится следующим образом. Выберем и зафиксируем . Формулы (3) позволяют по заданному номеру вычислять соответствующие коэффициенты в (2). Предполагается, что степени , , в формулах (3) априори вычислены и занесены в память компьютера для всех реально требуемых границ . При этом показатель степени соответствует математическому адресу ячейки памяти.

Коэффициентам и с номером , , ставятся в соответствие процессоры с номерами и соответственно. Процессор с номером , обращается к ячейкам с номерами и , в которых хранятся значения степени двойки необходимые для вычисления коэффициента , а процессор с номером к ячейкам с номерами и для вычисления коэффициента . Процессоры, работая синхронно и взаимно независимо, параллельно считают из памяти все степени двойки за время , затем вычислят искомые коэффициенты, причем одновременно для всех матриц рассматриваемого преобразования в формуле (2) с временной сложностью

,

здесь и ниже в скобках означает число процессоров.

Рекуррентная формула (2) представляется в виде произведений матриц.

Для удобства представления обозначим в формуле (2) первую матрицу, стоящую в произведении, через

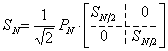. (4)

Индекс соответствует размеру квадратной матрицы. Выразим в соотношении (4) через и

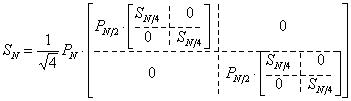. (5)

Представим вторую матрицу в выражении (5) в виде произведения

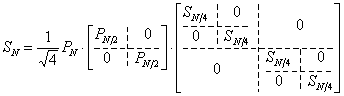. (6)

Далее, продолжая этот процесс, последовательно выражаем с помощью (4) , ,…, . Получаем (6) в виде произведения матриц

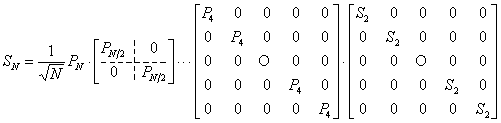. (7)

Если не учитывать диагональную структуру матриц, стоящих в (7), то можно воспользоваться естественным параллелизмом матриц. Все матрицы в (7) имеют размерность . Произведение матриц вычисляется с использованием схемы сдваивания.

Матрицы в произведении разбиваются по парам, затем внутри каждой пары они одновременно умножаются. На следующем шаге, как и на первом, матрицы также разбиваются по парам и одновременно умножаются в паре и т.д. Если число матриц нечётно, то матрица без пары не умножается, а остаётся в полученном произведении, пока на каком-то шаге их число не станет чётным. По указанной схеме произведение, состоящее из матриц, вычисляется за шагов. Умножение двух матриц, стоящих в паре, выполняется также c использованием схемы сдваивания. Искомая матрица состоит из элементов, каждому элементу вычисляемой матрицы , , ставится в соответствие процессоров. На первом шаге параллельно умножаются элементы -й строки на элементы -го столбца одновременно для всех значений . Все полученные парные произведения за шагов складываются по схеме сдваивания с тем же числом процессоров одновременно для всех .

Формула (7) разбивается на пар произведений матриц, каждой паре для умножения требуется процессоров, отсюда общее число процессоров .

Таким образом, на основе естественного параллелизма матриц, временная сложность алгоритма

. (8)

Число процессоров в (8) может быть существенно сокращено, это достигается следующим образом. Матрицы, входящие в (7), имеют одинаковую клеточную структуру. Клетки отличаются номерами коэффициентов и размером. Умножение матриц производится не по элементам матриц, а по их клеткам. В произведении выбираются клетки, которые имеют наименьший размер. Каждая клетка, в свою очередь, состоит из четырёх вложенных клеток, которые представляют собой матрицы. Матрицы отличаются от единичной четырьмя элементами, стоящими в левом верхнем углу.

Для вычисления произведения клетки на клетку требуется выполнить восемь алгебраических умножений и четыре алгебраических сложения. Произведения клетки на единичную клетку не требуют никаких алгебраических операций, так как единичная клетка с точностью до знака совпадает с единичной матрицей.

Эта особенность позволяет сократить число процессоров и число шагов при умножении матриц. На первом шаге в каждой паре вычисляется восемь произведений клеток, т.е. четыре клетки первой матрицы умножаются на две клетки второй матрицы . На втором шаге число произведений клеток – , на третьем – и т.д. При каждом шаге увеличивается в два раза показатель степени восьми, но и уменьшается в два раза количество пар произведений. Суммарное число произведений клеток во всех парах, с каждым шагом, изменяется следующим образом: , , , …, . На последнем шаге умножается наибольшее число клеток .

Для получения каждой клетки требуются выполнить восемь алгебраических умножений и четыре алгебраических сложений:

.

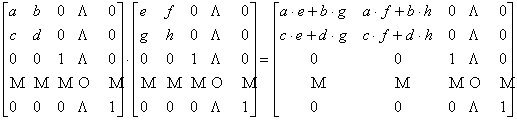Каждому произведению клеток ставится в соответствие восемь процессоров, которые параллельно умножают элементы, затем параллельно четыре процессора выполняют сложение.

Временная сложность схемы

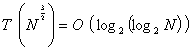. (9)

После построения матрицы вычисляется, непосредственно, само пилообразное преобразование на основе естественного параллелизма матриц с использованием схемы сдваивания. Временная сложность алгоритма с учётом построения матрицы преобразования составляет

. (10)

Заключение. Изложена схема вычисления пилообразного преобразования на основе естественного параллелизма. Получены логарифмические оценки временной сложности вычисления матрицы пилообразного преобразования (9) и вычисления преобразования в целом (10). Аналогичные алгоритмы ортогональных преобразований изложены в [5, 6].

литературА:

1. Миклошко Й. Связь между алгоритмами, программами и структурой параллельных ЭВМ. – В кн.: Алгоритмы математическое обеспечение и архитектура многопроцессорных вычислительных систем / Под ред. А.П. Ершова. – М.: Наука, 1982. – С. 6–36.

2. Солодовников В.И. Верхние оценки сложности решения систем линейных уравнений // Теория сложности вычислений. 1: Записки научных семинаров ЛОМИ АН СССР. Л., 1982. Т. 118. С. 159–187.

3. Ахмед Н., Рао К.Р.. Ортогональные преобразования при обработке цифровых сигналов: Пер. с англ. Т.Э. Кренкеля / Под ред. И.Б. Фоменко. – М.: Связь, 1980. – 248 с.

4. Прэт У.. Цифровая обработка изображений, в двух книгах. Книга 1: Пер. с англ. / Под ред. Д.С. Лебедева. – М.: Мир, 1982. – 311 с.

5. Ромм Я.Е., Забеглов В.В. Параллельные схемы некоторых дискретных ортогональных преобразований // Автометрия. – 2010. – Т. 46. – № 6. – С. 54 – 70.

6. Забеглов В.В. Компьютерно-ориентированные схемы минимизации временной сложности цифровой обработки сигналов при динамическом изменении отсчетов / Автореферат диссертации на соискание ученой степени кандидата технических наук. – Таганрог: ЮФУ. – 2010. – 20 с.