M.Sc. Ospanov M.G.
A.Baitursynov Kostanay State University, Kostanay
Image recognition. Algorithm Eigenface
Article devoted to the topic pattern
recognition, computer vision and machine learning. Presents an overview of the
algorithm, which is called eigenface.

Algorithm is based on the use of
basic statistical characteristics: mean (Matt. wait) and the covariance matrix;
the use of principal component analysis. We also touch on such concepts of
linear algebra, the eigenvalues (eigenvalues) and eigenvectors
(eigenvectors). And
in addition, to work in a multidimensional space.
Eigenface interesting
for me because the last 1.5 years I have been developing, including statistical
algorithms for different data sets, which often have to deal with all of the
above "pieces".
Tools
According to established, within my
modest experience, the procedure after a deliberation of the algorithm, but
before they are implemented in C / C + + / C # / Python etc., Must quickly ( as
possible ) to create a mathematical model and to test it, something to count.
This allows you to make the necessary adjustments to correct errors , to
discover what was not taken into account when thinking of the algorithm. To do
this, all I use MathCAD. MathCAD advantage in that, along with a lot of
built-in functions and procedures it uses classical mathematical notation.
Roughly speaking, it is enough to know the math and be able to write formulas.
Brief description of the algorithm
As with any algorithm in a series of
machine learning, eigenface must first train , is used for this training set
(training set), which is the image of people who we want to recognize. Once the
model is trained, we will provide some input image and as a result we obtain
the answer to the question: what image of the training sample is most likely
corresponds to an example of the input, or does not match any.
The task of the algorithm present an
image as the sum of the basic components (images):
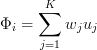
Where Фi - centered (excluding the average) i-th image of the
original sample, wj are the weight and uj eigenvectors
(eigenvectors or, in the framework of this algorithm, eigenfaces).

In the figure above, we obtain the
original image weighted summation of the eigenvectors and the addition of
medium. That is with w and u, we can recover any original image.
Training sample should be projected
into the new space (and the space is usually much more dimension than the
original 2x dimensional image), where each dimension will give a contribution
to the general idea. The principal component allows you to find a new basis for
the space so that the data in it is located, in a sense, optimal. To understand
just imagine that in the new space some dimension (aka principal components or
eigenvectors or eigenfaces) will "carry" more general information,
while others will only carry specific information. As a rule, the higher-order
dimension (corresponding to smaller eigenvalues) are much less
useful (in our case a useful understood as something that gives you a general
idea of the whole sample) information than the first dimension
corresponding to the largest eigenvalues. Leaving only dimension with useful
information, we have the space of attributes, where each image of the original
sample is presented in summary form. This is very simplistic, and is the idea of
the algorithm.
Further, having on hand a picture,
we can display it on the space created in advance and determine to which the
image of training sample, our example is the closest. If it is at a relatively
large distance from all the data, then the image is in general more likely to not
belong to our database.
For a more detailed description, I
suggest to contact list External links Wikipedia.
A small digression. The principal component has a fairly wide application. For
example, in my work, I use it to highlight in the data component of a certain
scale (temporal and spatial), direction or frequency. It can be used as a
method for data compression or the reduction method of the original dimension
of the multidimensional selection.
Literature:
1.
onionesquereality.wordpress.com/