M.Sc. Ospanov M.G.
A.Baitursynov Kostanay State University, Kostanay
Image
recognition. Creating a model
Compile the training sample used
Olivetti Research Lab's (ORL) Face Database. There are 10 photos of 40
different people:

To describe the implementation of
the algorithm I will insert screenshots here with functions and expressions of
MathCAD and comment on them. Come on.
1. 
faceNums sets the vector numbers of
persons that will be used in training. varNums specifies a version number (as
described in our database 40 directories in each of 10 image files of the same
person). Our training set consists of 4 images.
Next, we call ReadData. It
implements the sequential reading of data and transfer images to vector
(function TwoD2OneD):

Thus the output have a matrix in
which each column D is "unfolded" into a vector image. Such a vector
can be regarded as a point in a multidimensional space, where the dimension is
determined by the number of pixels. In this case, the image size 92h112 give
vector of 10304 elements or specify a point in 10,304-dimensional space.
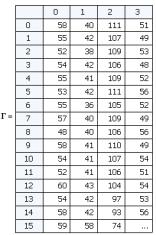
2. Necessary to normalize all the
images in the training sample by subtracting the average image. This is done in
order to keep only the unique information, removing common to all image
elements.
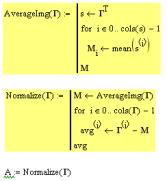
Function finds and returns
AverageImg mean vector. If we do this vector "turn back" in the
image, we see "the average person":

3. The next step is the calculation
of the eigenvectors (they eigenfaces) u and w weights for each image in the
training set. In other words, a transition into a new space.

Compute the covariance matrix , and
then find the principal components (they are eigenvectors) and consider the
weight. Those who are acquainted with the algorithm closer vedut in math. The
function returns a matrix of weights, the eigenvectors and eigenvalues. It is
necessary to display the data in the new space . In our case, we work with the
4 -dimensional space, the number of elements in the training set, the remaining
10304 - 4 = 10300 degenerate dimension, we do not consider them.
Eigenvalues we
generally do not need, but it can be traced back some useful information. Let's
look at them:
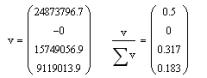
Eigenvalues actually
show the variance for each of the axes of the principal components (each
component corresponds to one dimension in space). Look at the right expression
vector programming current = 1, and showing the contribution of each element in
the total data variance. We see that 1 and 3 principal components give a total
of 0.82. Ie 1 and 3 contain 82% of the dimension of the entire information.
Second dimension is minimized, and the fourth shall be 18% of the information
and we do not need it.
Literature:
1. onionesquereality.wordpress.com/