Д. физ-мат. наук, проф. Геворкян Р.С., Асратян М.Г.

Институт механики НАН РА, Армения

К АСИМПТОТИЧЕСКOМУ РЕШЕНИЮ ЭЛЛИПТИЧЕСКИХ

УРАВНЕНИЙ СТАЦИОНАРНОЙ ТЕПЛОПРОВОДНОСТИ ДЛЯ ТОНКИХ ПОЛОС KОНЕЧНЫХ РАЗМЕРОВ

В работе строится алгоритм для решения задачи пограничного слоя полосы конечной длины с заданными на продолных краях oднородными условиями стационарной теплопроводности , исходя из асимптотического решения внутренней задачи изотропной полосы бесконечной длины, когда на ее продольных краях заданы условия первой краевой задачи теории теплопроводности. Приводится пример, когда на поперечных краях (торцах) полосы заданы условия первой краевой задачи теории теплопроводности.

При асимптотическом методе решения возмущенных геометрическим малым параметром краевых задач теорий упругости, магнито-электро-термо- упругости, теплопроводности (и др). для тонких тел [1-14], решение складывается из двух решений: _– внутреннего (пронизывающего, основного) решения [1,2,5–13]., которое удовлетворяет граничным условиям, заданным на лицевых поверхностях тонкого тела и доминирует внутри области занимаемой телом. Такие решения также называют внешними асимптотическими разложениями [9] в отличие от решения задачи в пограничном слое , которое на лицевых поверхностях тонкого тела удовлетворяет соответствующим однородным (нулевым) условиям и, в сумме с решением внутренней задачи, удовлетворяет граничным условиям, заданным на торцах пластины. Для тонких продолговатых тел оно быстро затухает по направлению внутренней нормали к поверхности торца.

В работе асимптотическим методом решена первая краевая задача стационарной теплопроводности для изотропной полосы бесконечных размеров (внутренняя задача полосы конечных размеров), за тем, на основе этого решения, построено решение задачи пограничного слоя для полосы конечных размеров, когда на ее продольных краях заданы однородные (нулевые) краевые условия второй краевой задачи стационарной теплопроводности (удельная плотность потока теплоты).

1. Общий интеграл асимптотического решения двумерного уравнения теории стационарной теплопроводности. Рассмотрим двумерное уравнение стационарной теплопроводности [14] (уравнение Лапласа) в прямоугольной области-полосе (бесконечной длины) и ширины 2h плоскости

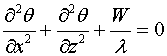(1.1)

B уравнении (1.1) перейдем к безразмерным координатам по формулам 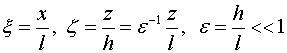(1.2)

получим

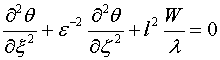(1.3)

Уравнение (1.3) сингулярно возмущена геометрическим малым параметром . Его асимптотическое решение должно складываться из двух слагаемых: из решения внутренней, основной задачи и согласованного с ним решения задачи в пограничном слое вблизи торцов [1–13].

Решение внутренней задачи ищется в виде асимптотического разложения 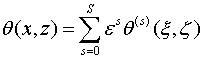(1.4)

одновременно, заданную в уравнении (1.1) функцию (в частности, удельняя плотность источника тепла) представим в виде 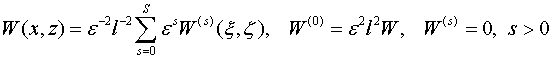(1.5)

Такое представление обеспечивает влияние функции 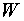на асимптотическое

решение краевой задачи начиная с первого шага итерационного процесса.

Подставив (1.4),(1.5) в (1.3) и приравняв коэффициенты при 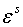в левой и правой частях равенства получаем разрешающее уравнение

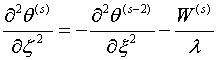(1.6)

общий интеграл которого имеет вид

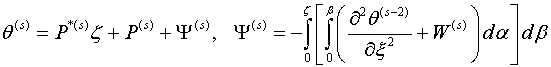(1.7)

где 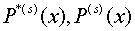произвольные функции интегрирования.

Общее решение (1.7) позволяет решить краевые задачи стационарной теплопроводности для полосы бесконечной длины, когда на ее продольных краях заданы условия первой и смешанной краевых задач [14].

2. Решение первой краевой задачи для полосы бесконечной длины и алгоритм построения решений типа погранслоя. Пусть на продольных краях полосы заданы значения искомой функции (значения температуры – в первой краевой задаче)

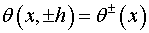(2.1) Удовлетворив условиям (2.1) однозначно определяем функции интегрирования и искомую функцию в виде рекуррентной формулы

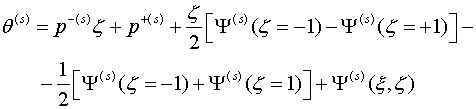(2.2)

Вычислив четыре шага итерации при 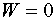, с учетом (1.4) получаем

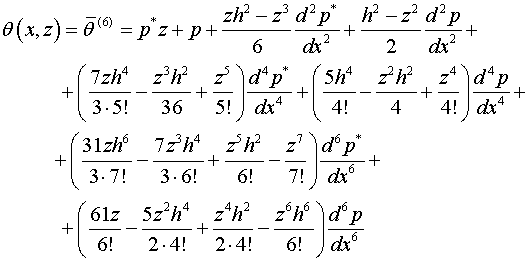(2.3)

Выведенное асимптотическим методом решение (2.3) замкнутое, т.е. математически точное для полосы бесконечных размеров, если заданные на продольных краях полосы функции 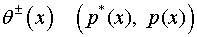являются многочленами степени не выше 6 (шести). Если же они произвольные достаточно гладкие непрерывные функции с изменяемостью 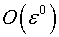, то асимптотическая точность решения (2.3) составляет .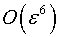

Учитывая вышеизложенное попробуем с помощью решения внутренней задачи (2.3) построить решения задач типа пограничного слоя для полос конечных размеров. С такой целью поставим задачу: Какими должны быть заданные на продольных краях 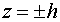полосы конечной длины температурные функции 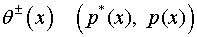, чтобы удельная плотность

потока теплоты на этих краях (линиях) была равна нулю? т.е.

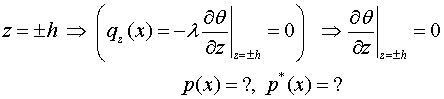(2.4)

Удовлетворив условиям (2.4) получаем систему из двух независимых дифференциальных уравнений с постоянными коэффициентами относительно . Kаждое из них шестого порядка

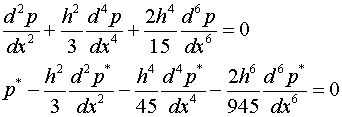(2.5)

Дифференциальные уравнения (2.5) легко приводятся к квадратурам [15] и их общие интегралы имеют следующий вид:

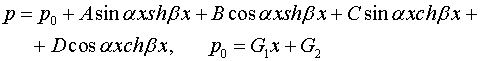
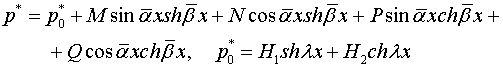
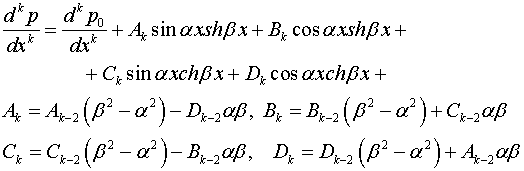(2.6)

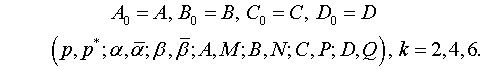
В формулах (2.6) – мнимые и действительные части корней характеристических уравнений системы (2.5), которые аналитически определяются известным образом [15], в частности, формулой Кордано, поскольку характеристические уравнения системы (2.5) бикубические.

Таким образом асимптотическим методом с точностью выведено общее решение уравнения нестационарной теории теплопроводности (2.3), (2.6), которое на продольных краях полосы удовлетворяет условиям отсутствия потока теплоты (2.4) и содержит двенадцать постоянных интегрирования – которые должны определиться из, заданных на торцах полосы конечной длины, граничных условий первой, второй или смешанной краевых задач теории стационарной теплопроводности.

Эти граничные условия в общем случае должны быть непрерывные функции поперечной координаты . Поскольку общий интеграл (2.3), (2.6) является полиномом по , целесообразно, чтобы на правом и левым торцах условия тоже были заданы (или представлены) в полиномиальном виде. Пусть они имеют вид

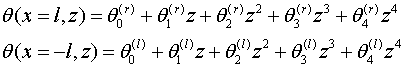(2.7)

Подставив (2.6) в (2.3) и удовлетворив граничным условиям (2.7) получим систему линейных алгебраических уравнений относительно постоянных интегрирования , решение которой дает

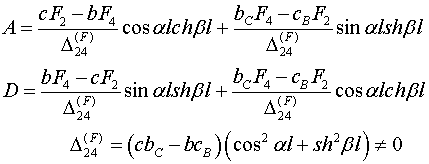
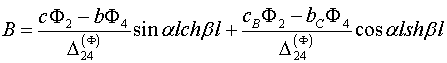
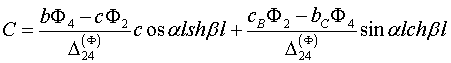
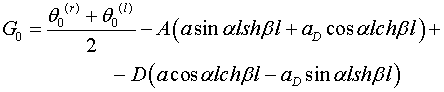(2.8)

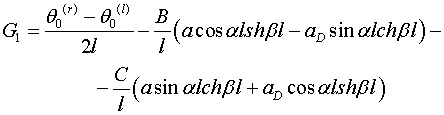
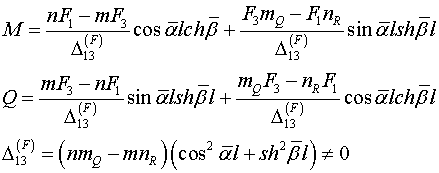
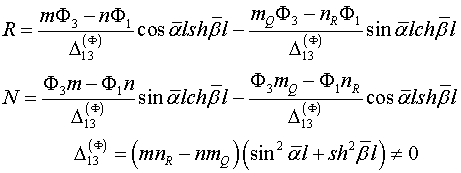
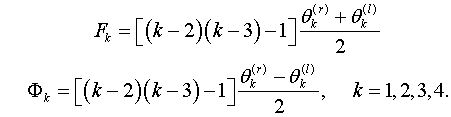
В формулах (2.8) обозначены

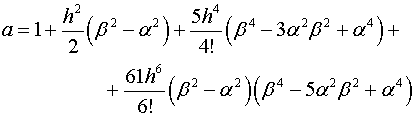
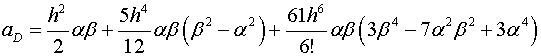
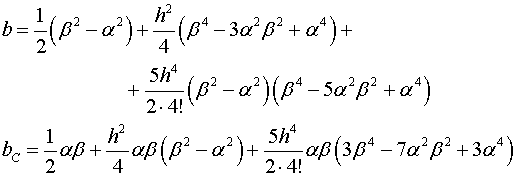
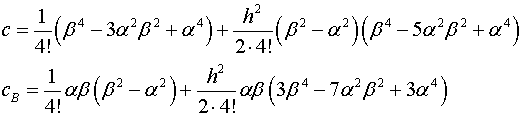(2.9)

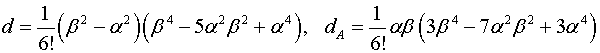
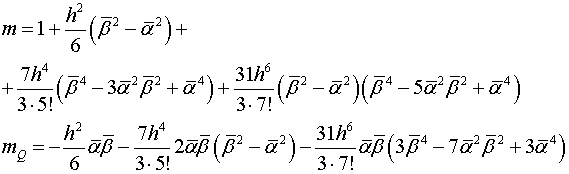
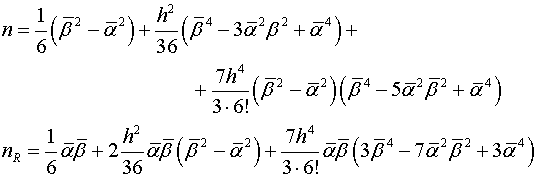
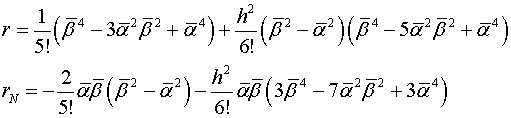
Таким образом температурная функция определяемая формулой (2.3) удовлетворяет уравнению теории стационарной теплопроводности (1.1) (при ) с асимптотической точностью [13]. А когда функции определяются формулами (2.6), при условиях (2.8),(2.9), на продольных краях полосы математически точно удовлетворяет однородным условиям (2.4), а на торцах () полосы также математически точно удовлетворяет полиномиальным условиям (2.7). Этот же общий интеграл (2.3),(2.6) позволяет определить постоянные интегрирования, удовлетворив на торцах полосы граничные условия второй или смешанной краевых задач теории стационарной теплопроводности.

Заметим, что предлагаемый алгоритм построенния решения задачи пограничного слоя существенно отличается от существующих других методов решений аналогичных задач [5,11,12,13]. Метод аналитический и несложный для практического применения. Он применим также для построения решений задач пограничного слоя в статической теории упругости.

Литература

1. Агаловян Л. А. О структуре решения одного класса плоских задач теории

упругости анизотропного тела// Механика. Ереван: Изд-во ЕГУ, 1982.C.7–12.

2. Агаловян Л.А., Геворкян Р.С. Неклассические краевые задачи пластин с общей анизотропией //Сб. тр. 4-го Всес. Симп. по механике конструкций из композиционных материалов. Новосибирск: Наука, 1984. С.105–110.

3. Агаловян Л. А. Асимптотическая теория анизотропных пластин и оболочек. М: Наука.Физматлит, 1997. 414с.

4. Агаловян Л. А., Геворкян Р. С. Неклассические краевые задачи анизотропных слоистых балок, пластин и оболочек Ереван: Гитутюн, 2005. 468с.

5. Гольденвейзер А.Л. Теория упругих тонких оболочек. М.: Наука,1976. 512с.

6. Асратян М.Г., Геворкян Р.С., Саргсян М.З. Асимптотическое решение краевой задачи электроупругости для пьезокерамического в плане неоднородного тонкого тела//В кн. Проблемы механики деформируемого твердого тела. Ереван, 2012. С.65-74.

7. Зино И.Е., Тропп Э.А. Асимптотические методы в задачах теории теплопроводности и термоупругости. Л.: Изд-во ЛГУ, 1978. 224 с.

8. Геворкян Р.С. Асимптотические решения (связанных) динамических задач термоупругости для изотропных пластин//ПММ.2008.Т.72. Вып.1. С.148-156.

9. Немировский Ю.П., Янковский А.П. Метод асимптотических разложений решений задачи стационарной теплопроводности слоистых анизотропных неоднородных пластин. // ПММ. 2008. Т. 72. Вып. 1. С. 157–175.

10. Геворкян Р.С., Саркисян А.Г. К задаче теплопроводности анизотропных в плане неоднородных тороидальных оболочек.// Материалы IX Международной научно - практической конференции «Репортаж научных идей-2013». - Часть 22. Математика. Прага – 2013. С. 10-21.

11. Агаловян Л. А. Упругий пограничный слой для одного класса плоских задач // Механика. Ереван: Изд-во ЕГУ, 1984. C. 51-58.

12. Геворкян Р. С. Асимптотика пограничного слоя для одного класса краевых задач анизотропных пластин // Изв АН Арм. ССР. Механика. 1984 Т. 37.№ 6.

С. 3–15.

13.Ломов С.А. Введение в общую теорию сингулярных возмущений. М.: Наука, 1981. 398 с.

14. Лыков А.В. Теория теплопроводности. М.: Гостехиздат, 1952. 392с.

15. Корн Г, Корн Т. Справочник по математике для научных работников и инженеров.М.: «Наука»,1973. 832с.