Математика / 5. Математическое моделирование

К. пед. н. Бондар М. В., Боровик В.С.

Вінницький торговельно-економічний інститут Київського національного торговельно-економічного університету, Україна

Прогнозування із використанням рівняння регресії

Використання економетричних методів допомагає отримати точні, вірогідні, надійні та однозначні результати та висновки. Математична обробка даних за допомогою комп’ютерної техніки є необхідною складовою будь-якого дослідження. За допомогою економетричних методів та комп’ютерної техніки можна визначати форми та тісноту зв’язку між факторною та результативною ознакою.

Дане дослідження є актуальним, тому що за допомогою регресійних рівнянь можна отримувати точні результати, комп’ютерні технології постійно розвиваються. Незважаючи на все більш зростаючу зацікавленість дослідників та науковців до проблеми вибору та розробки методів прогнозування, все ж таки нерозкритими і дискусійними залишаються багато питань.

Тема методів прогнозування в країнах з перехідною економікою дуже актуальна. Вона розглянута в працях вітчизняних та російських вчених: Николаєвої Е.П, Боровика В.П, Барсегяна А.А, Єсєнькина Б.С. та інших.

Регресійний аналіз (англ. regression analysis) – це метод визначення відокремленого і спільного впливу факторів на результативну ознаку та кількісної оцінки цього впливу шляхом використання відповідних критеріїв.

Регресійний аналіз проводиться на основі побудованого рівняння регресії і визначає внесок кожної незалежної змінної у варіацію досліджуваної (прогнозованої) залежної змінної величини.

Основним завданням регресійного аналізу є визначення впливу факторів на результативний показник (в абсолютних показниках). Передусім для цього необхідно підібрати та обґрунтувати рівняння зв'язку, що відповідає характеру аналітичної стохастичної залежності між досліджуваними ознаками. Рівняння регресії показує як в середньому змінюється результативна ознака (Y_х) під впливом зміни факторних ознак (х_і). У загальному вигляді рівняння регресії можна представити:

Y_х = f (x₁, x₂,…,x_n),

де Y_х – залежна змінна величина; х – незалежні змінні величини (фактори) [3].

Визначення параметрів множинної регресії вимагає трудомістких розрахунків із застосуванням комп'ютерних інформаційних систем. Однак одержані результати будуть достовірними і можуть широко використовуватися в економічній та управлінській діяльності насамперед для складання довгострокових прогнозів. Відомо, що однофакторна модель придатна для короткострокових прогнозів (на 2-3 роки).

Парний регресійний аналіз заснований на використанні рівняння прямої лінії:

y = a + bx,

де y – оцінювана чи прогнозована залежна перемінна (результативна ознака); a – вільний член рівняння; x – незалежна перемінна (факторна ознака), використовувана для визначення залежної перемінної; b – коефіцієнт регресії, що вимірює середнє відношення відхилення результативної ознаки від його середньої величини до відхилення факторної ознаки від його середньої величини на одну одиницю його виміру – варіація y, що приходиться на одиницю варіації x.

Коефіцієнти a і b розраховуються на основі спостережень величин y і x за допомогою методу найменших квадратів [1].

Наприклад, вводиться гіпотеза, що між фактором Х та Y існує лінійна стохастична залежність У = b₀ + b₁x. Ми маємо вихідні дані (рис. 1) та проводимо певні проміжні розрахунки (С2:М12). Прогнозні значення обчислюємо у 15-у рядку.

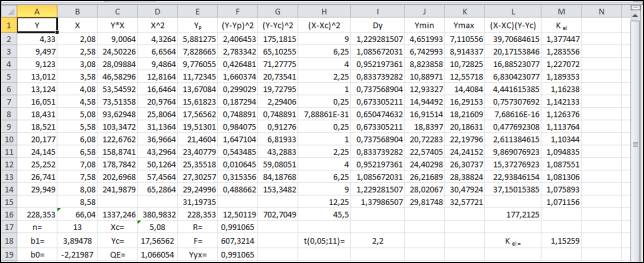
Рис. 1. Вихідні дані та розрахунки для прогнозування

На основі вихідних даних та всіх розрахунків будуємо діаграму та додаємо лінію тренда. Лінію тренда будуємо лише для Y.

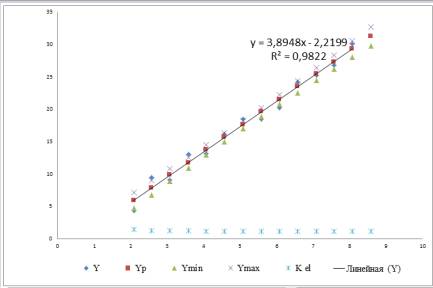
Рис. 2. Побудована діаграма та лінія тренда

Отже, метод регресійного аналізу вважається найдосконалішим з усіх використовуваних нині нормативно-параметричних методів. Регресивний аналіз надає можливість знайти емпіричну форму залежності ціни від техніко-економічних параметрів товарів і виробів. При цьому він виступає в ролі цільової функції параметрів. Метод регресійного аналізу особливо ефективний за умови здійснення розрахунків за допомогою сучасних інформаційних технологій і систем.

Література:

1. Кириленко О.Н. Використання методів математичної статистики для прогнозування розвитку ринку логістичних послуг в Україні в сучасних умовах [Електронний ресурс] / О.Н. Кириленко, О.В. Кудрицька / режим доступу : http://jrnl.nau.edu.ua/index.php/ppei/article/viewfile/462/450

2. Калініченко А.В. Прогнозування за допомогою функцій регресії [Електронний ресурс] / А.В. Калініченко, Ю.В. Шмиголь, К.Д. Костоглод / режим доступу: http://khntusg.com.ua/files/sbornik/vestnik_104/02.pdf

3. Купалова Г.І. Теорія економічного аналізу : навч. посіб. / Г.І. Купалова – К. : Знання, 2008. – 639 с.