А.И. Долгарев

2-ПОВЕРХНОСТИ 4-МЕРНОГО ЕВКЛИДОВА ПРОСТРАНСТВА

2-параметрические поверхности 4-мерного евклидова пространства могут иметь размерность от 1 до 3. Линия может рассматриваться как пересечение 2-пераметрических поверхностей. Существуют цилиндрические поверхности размерности 3, они не более чем 2-параметрические.

Часто мерные поверхности евклидова мерного евклидова пространства , , изучаются как погружения мерного многообразия в , , это поверхность-график, [1, 2], или явно заданная поверхность. Бытует мнение о том, что существует нормалей к поверхности , т.е. поверхность обладает мерной нормальной плоскостью. Это не всегда верно. В [3, c. 184 – 186], внутри раздела 15, намечен подход к заданию мерных поверхностей в мерном евклидовом пространстве , . Развивая идеи изучения мерных поверхностей в мерных пространствах, изложенные в [2, 3], рассматриваем поверхности, заданные несколькими скалярными функциями. Рассматривается регулярная поверхность, , она является подмногообразием гладкого многообразия . Многообразие может описываться одной функцией , или несколькими функциями, [2, c. 180 – 182]. Достаточно поверхности изучать в некотором фиксированном репере, считая формулы замены реперов дифференцируемыми.

1. Гиперповерхности и цилиндрические поверхности

1.1. Виды поверхностей

Евклидово пространство обладает векторным пространством , пусть его базис = ; пространство состоит из кортежей действительных чисел длины :

= .

Поверхность в есть образ мерного многообразия , в паре с погружением . Погружение и поверхность записывается функцией

.

Если , то, разумеется, поверхность описывается векторной функцией

, (1)

компоненты не зависят от . Пусть точка поверхности , . Всякая прямая , , проходящая через точку в направлении вектора , лежит на поверхности . Поверхность является цилиндрической, содержащей плоскость . Размерность плоскости равна . Векторы касательных

, , ,

к линиям поверхности (1) независимы. векторов и векторов вместе с точкой порождают касательную плоскость

=

размерности к поверхности (1) в ее обыкновенной точке ; размерность поверхности равна . Тем самым, на основе [4, лемма 4], выполняется:

1. ТЕОРЕМА. Всякое погружение определяет в пространстве параметрическую поверхность размерности . Поверхность размерности является либо гиперповерхностью, либо цилиндрической поверхностью. #

Кроме указанных двух видов поверхностей евклидовых многомерных пространств существуют еще поверхности, задаваемые несколькими скалярными функциями

; , ,

как подмногообразия многообразия , см. [2, c. 182 – 184; 3, c. 184 – 186].

1.2. Поверхности пространства , заданные одной явной функцией.

Погружения могут быть 1,2,3-параметрическими.

(а) 3-параметрические поверхности . Погружение описываются одной явной функцией или векторной функцией

= .

В окрестности всякой обыкновенной точки имеется 3 независимых вектора касательных: , , ; касательная плоскость 3-мерна,

=

и поверхность 3-мерна. Вектором нормали, согласно [4], является

, (2)

нормаль поверхности есть = . Так как , то единичный вектор нормали таков

.

(б) 2-параметрические, т.е. 2-порожденные поверхности описываются явной функцией и векторной функцией:

= .

Касательные векторы: , и ; касательная плоскость

=

имеет размерность 3 и поверхность 3-мерна. Вектор нормали , нормаль такова: = .

(в) 1-параметрические, 1-порожденные поверхности описываются явной функцией: и векторной функцией

= .

Касательные векторы , ; касательная плоскость = размерности 3 и поверхность имеет размерность 3. Вектор нормали и нормаль 1-параметрической поверхности есть = .

Можно рассматривать цилиндрическую поверхность = , (параметр от параметра не зависит) она 1-параметрическая и 2-мерная. Ее касса-

тельная плоскость: = , нормали

2- и 1-порожденные поверхности являются цилиндрическими. Как видно, не всякая 1-параметрическая поверхность есть линия, возможно это цилиндрическая поверхность. Так как касательные плоскости указанных выше поверхностей 3-мерны, то все эти поверхности 3-мерны. Выше изложенные факты суммируются утверждением

2. ТЕОРЕМА. [4, п. 4] Явно заданная поверхность , , пространства обладает единственной нормалью во всякой своей обыкновенной точке

= . #

В [4] указаны метрическая форма и форма кривизны поверхностей , заданных одной явной скалярной функцией и найдены, [4, теорема 13], выражения коэффициентов формы кривизны через коэффициенты метрической формы поверхности. Значит явно заданная поверхность определяется однозначно, с точностью до положения в пространстве, своей метрической формой. Тем самым, повышается значение метрической формы поверхности. В теории поверхностей важно не только знать, сколько касательных и нормальных векторов имеет поверхность, но и предъявлять эти векторы, т.е. записывать их в тех координатах, в которых задана поверхность.

2. Поверхности размерности 2 в пространстве размерности 4.

2.1. Поверхности меньшей размерности

Об мерных поверхностях в мерном пространстве, , в [3, c. 184 – 186] говорится следующее. Поверхность есть непустое пересечение поверхностей размерности . Нормали этих гиперповерхностей линейно независимы и порождают вместе с точкой поверхности нормальную плоскость поверхности . В [2, c. 180 – 182] мерная поверхность мерного пространства задается функциями от параметров и может быть описана векторной функцией:

, где .

Известно, что плоскости мерного пространства, , могут не пересекаться, могут в пересечении иметь точку, прямую, или плоскость вплоть до размерности . Это относится и к пересечению мерных поверхностей в пространстве. Условие непустоты пересечения поверхностей в предыдущем абзаце определяет не только мерную поверхность, а все поверхности размерности не больше .

2.2. Поверхность в , заданная двумя функциями

Рассмотрим в 2-параметрическую поверхность , описываемую функцией

= , , . (3)

Это многообразие с наименьшим возможным числом параметров, определяющим поверхность в евклидовом пространстве наименьшей размерности, в котором поверхность может быть задана двумя скалярными функциями. Можно рассматривать цилиндрическую поверхность = , (параметр от параметра не зависит), она 1-параметрическая и 2-мерная. Укажем векторы касательных и нормалей к поверхности их координатами. Векторы касательных линий поверхности (3) таковы

, (4)

и для их компонент выполняется условие:

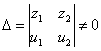. (5)

В точке = поверхности определена касательная плоскость

= ,

она 2-мерна. В векторном пространстве пространства существует два неколлинеарных вектора нормалей к плоскости . Один из них выберем по аналогии с (2):

= . (6)

Другой вектор нормали к поверхности отыскивается из условий :

. (7)

Векторы и неколлинеарны, нормальная плоскость поверхности в точке такова

=, (8)

плоскость 2-мерна. Модули векторов нормали:

, . (9)

2.2. Фундаментальные формы поверхности

Метрической формой поверхности является

=, ; (10)

коэффициенты метрической формы таковы:

, , . (11)

3. ТЕОРЕМА. Детерминант метрической формы поверхности связан с функциональным детерминантом (5) поверхности и равен

. # (12)

В координатах на поверхности рассматривается кривая

,

где естественный параметр кривой. Векторы производных функции :

,

. (13)

Векторы вторых производных: , , . Нормальная кривизна линии относительно нормали (6) равна

= =

= . (14)

а нормальная кривизна линии относительно нормали (7) равна

= =

= +

+. (15)

Модули векторов нормали есть (9). Выполняются равенства:

= , = .

Форма кривизны первого вида поверхности записана в (14) и форма кривизны второго вида поверхности записана в (15). Коэффициенты метрической формы есть (11), коэффициенты форм кривизны поверхности соответственно равны

= , = , = (16)

для формы кривизны поверхности первого вида;

= , = ,

=

для формы кривизны поверхности второго вида. Значение есть (12). Во введенных обозначениях:

= , = .

Не видно, выражаются ли коэффициенты форм кривизны через коэффициенты метрической формы поверхности в случае задания поверхности несколькими функциями.

3. Многообразие в как линия.

3.1. Уменьшение числа параметров многообразия,

заданного несколькими скалярными функциями

Многообразие (3), описанное двумя скалярными функциями , , согласно п. 2.1, может быть линией. Оно содержит два следующих 2-параметрических подмногообразия

: = , : = .

Каждое из них является цилиндрической поверхностью в пространстве . Поверхность является цилиндрической с образующими, параллельными координатной оси . Поверхность тоже цилиндрическая, ее образующие параллельны оси . Общие точки поверхностей и могут составлять линию пересечения двух цилиндрических поверхностей:

: = ,

она описывается системой функций

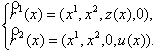: (17)

Значит, имеется выражение параметров через некоторый параметр , т.е. линия

==. (18)

Рассматриваем ее как линию пересечения .

3.2. Линия пересечения цилиндрических поверхностей

Сначала получим вектор касательной линии (17): =. Цилиндрическая поверхность имеет касательные векторы

, ,

содержит прямую , определяемую вектором , точка многообразия , см. п. 1.1. Уравнение касательной плоскости к :

, где

произвольная точка пространства обозначена . Уравнение не содержит четвертой координаты, плоскость касается цилиндрической поверхности пространства , вектор нормали к касательной плоскости таков . Аналогично, имеется уравнение касательной плоскости поверхности

,

ее нормальный вектор . Вектор , нормальный векторам и , получается по аналогии с вектором (7) из п. 2.1, это вектор касательной к линии (17) пересечения поверхностей и : . Выполняются равенства , . Уравнения касательной к линии пересечения:

.

Рассматриваем линию в естественной параметризации . Известно, что вектор касательной к линии, заданной в естественной параметризации, является единичным, а вектор второй производной перпендикулярен вектору касательной, он определяет главную нормаль линии. Векторы касательных к поверхностям и таковы:

, , , .

По (18) имеем вектор касательной к : . Находим:

.

Запишем вектор в виде двух слагаемых:

= ,

=, =+.

Вектор перпендикулярен вектору касательной . Вектор имеет следующий вид

= + = ,

см. (4), каждое его слагаемое лежит в касательной плоскости к соответствующей цилиндрической поверхности (3), он не может быть составляющей нормали к линии. Поэтому остается вектор кривизны

= ,

напоминающий форму нормальной кривизны (14) линий на поверхности . Кривизна линии пересечения равна = Таким образом, приходим к утверждению

4. ТЕОРЕМА. Поверхность = (3), заданная двумя скалярными функциями , , имеющая форму кривизны (16), как линия пересечения (17) двух цилиндрических поверхностей, имеет кривизну , вычисляемую по коэффициентам (18) формы (16). #

Из двух нормальных кривизн линий на поверхности (3), относительно векторов нормалей (6) и (7), нормаль (6) содержится как часть главной нормали линии (18).

Список литературы

1. Иванова-Каратопраклиева И., Марков П.Е., Сабитов И.Х. Изгибание поверхностей. III. – Фундаментальная и прикладная математика, том 12. (2006), № 1, С. 3 – 56.
2. Иванов А.О., Тужилин А.А. Лекции по классической дифференциальной геометрии. – М.: Новая университетская библиотека, 2009 – 233с.
3. Торп Дж. Начальные главы дифференциальной геометрии. Волгоград: «Платон», 1998 – 360с.
4. Долгарев А.И. Многомерные поверхности I. Выражение коэффициентов второй квадратичной формы евклидовой поверхности через коэффициенты первой квадратичной формы.// Materialy X Miedzynarodowej naukowi-praktycznej konferencji “Moderni vymozenosti vedy – 2014”, dil 34. Matematyka. Fizyka. Praga. Publiching House “Education and Skience”. s.r.o. – 2014. С. 30 – 40.