Математика 5. Математическое моделирование

А.Айдосов, д.т.н., проф. КазНУ им. Аль Фараби

Н.С.Заурбеков, д.т.н., проф., зав.кафедрой ИТ АТУ

Н.Д.Заурбекова, к.т.н., КазНТУ им. К.Сатпаева

Бейбитжан М.Б. - магистрант ИС, АТУ

Женисбек М. - магистрант ИС, АТУ

Алматинский технологический университет, Алматы, Казахстан

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ОЦЕНКИ ВЛИЯНИЯ ВЫБРОСОВ В АТМОСФЕРУ ПРОМЫШЛЕННОГО РЕГИОНА НА ЗДОРОВЬЕ НАСЕЛЕНИЯ

Для оценки влияния состояния окружающей среды на заболеваемость населения, использовались математико-статистические модели 4-х типов - две модели для числовых переменных и две модели для нечисловых переменных. Модели для числовых переменных. Выделялось множество территорий - S, S, ..., S, множество факторов среды - X, X, ..., X, множество показателей, характеризующих заболеваемость – у₁, y,..., y, половозрастные группы населения -U,U,...,U, последовательные интервалы времени (как правило, календарный месяц) - t=1,2, ... ,n. Определялись y (U, Sdt) - как значение показателя заболеваемости y для группы населения U на территории Sd в интервале времени t; X(Sdt) - среднее значение фактора X на территории Sd в интервале времени t. Факторам X, X, ..., X соответствуют характеристики загрязнения атмосферного воздуха пылью, двуокисью азота и т.п. Показатели y, y, ..., y представляют собой формируемые специальным способом характеристики здоровья населения:- заболеваемость; - смертность; - и т.д.

Группы U, U, ..., U определялись по полу, возрасту, району проживания, профессиональной принадлежности и т.д.

Анализ зависимостей выполнялся поэтапно в интерактивном человеко-машинном режиме. Каждый этап реализовался по схеме:

1. Фиксируется единственная группа U;

2. Фиксируется единственный показатель y и набор факторов X, X, ..., X - часть или весь набор контролируемых факторов;

3. Фиксируется подмножество территорий и подмножество временного интервала;

4. Из базы данных формируются файлы по заданной группе, показателю, факторам, территориям и временным интервалом;

5. Формируются корреляционные поля для каждой пары из множества переменных X, X, ..., X, y, где коэффициент корреляции Пирсона вычисляется по формуле:

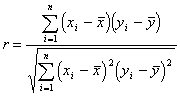(1)

где х, - выборочные средние арифметические, n - объем выборки;

6. Строятся уравнения линейной регрессии и оцениваются его коэффициенты, и параметры:

y(USt)= (2)

Модели для нечисловых переменных. Рассмотрим меры связи для двух переменных. Введем обозначения, с двумя выходами для переменных А и В, имеющих соответственно i и j уровни категорий, где fml -есть частота появления одновременно категорий Am и Bl.

f - это общий итог всех рассмотренных случаев или математически:

(3)

Для определения связи и независимости в таблицах сопряженности (LxJ) необходимо: в случае независимости наших переменных должны выполняться следующее соотношения:

для всех i,j. (4)

Обозначая PJ вероятность того, что случайно выбранный индивид попадает в ячейку (ij), просто получить условие независимости, а именно, если А и В независимы, то

PJ= P PJ , i = 1,2, ... , I; j=1,2, ... , J. (5)

оценка PJ служит lJ:

lJ= (6)

Отсюда для критерия Х получаем:

Х= 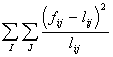(7)

c (i-1)x(j-1) со степенями свободы для проверки независимости.

Распределение Х лишь приблизительно соответствует Х распределению, но оно хорошо работает для fJ>3. Имеются следующие меры связи, основанные на Х:

V - Крамера и T - Чупрова

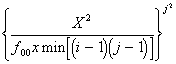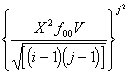V=; T= (8)

Из других мер назовем - Гудмена и Краскала:

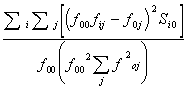= (9)

меры , и .

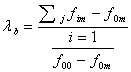, (10)

где f-наибольший вход в i-строке, f - наибольший из итогов по столбцам.

Анализ таблиц сопряженности с более, чем двумя входами сложен и очень громоздкий, поэтому в практике почти не используется.

Для оценки и анализа влияния социально-гигиенических условий жизни населения на частоту обращаемости за медицинской помощью в амбулаторно-поликлинические учреждения получались таблицы сопряженности Sxr, где r - количество (категорий), принимаемых переменной отклика; S - количество значений, принимаемых факторной переменной.

Для проверки гипотезы о независимости (не влиянии социально - гигиенических факторов по обращаемости) использовалась статистика со степенями свободы:

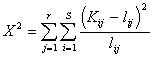; (11)

где nij - фактические частоты таблицы сопряженности; lij - теоретические ожидаемые частоты при условиях независимости признаков.

Для измерения силы связи использовались коэффициенты:

P= , контингенции С= , (12)

также V - Крамера, - Ксендала, - Стюарта.

Для определения значимости влияния отдельных социальных факторов на уровень заболеваемости были применены логарифмические линейные модели для таблиц сопряженности.

Поскольку истинные вероятности в совокупности неизвестны, остается использовать наблюдаемые частоты ячеек в качестве их оценок. В результате то, что извлекается из модели, находит разумное объяснение через различия в наблюдаемых частотах ячеек. Тогда модель можно интегрировать в терминах вероятностей ячеек, которые, конечно, обязаны лежать между 0 и 1. Отсюда следует, что простейший путь построения модели заключается в том, чтобы работать не с вероятностями, а с какими-нибудь функциями от вероятностей, причем такими, которые не ограничены и имеют своим минимальным значением -, а максимальным +.

Для дихотомических факторов, у которых вероятности категорий 1 и 2 равны соответственно Р и (1-Р) , можно работать потенцируя обе части, избавившись от n и получить или, разрешая относительно Р: . Функция Х известна под именем “логит” или логарифмы преобладания.

Рассмотрим некоторые модели для таблицы 2x2.

Допустим, имеется таблица 2x2 для категорированных переменных А и В и мы хотим проверить гипотезы:

1) A встречается чаще A;

2) B встречается чаще B;

3) сочетания A B и A B встречаются чаще, чем можно было бы ожидать, если бы переменные А и В были независимы.

Теперь нужен математический метод, который позволяет количественно сравнить относительную важность этих трех эффектов и выявить случаи, когда эффекты следует признать реальными, а когда стоит приписать их случайным отклонениям [1-6]. Такой метод предполагает использование модели, записанной относительно натуральных логарифмов вероятностей ячеек .

Рассмотрим модель lcmI, loge от

, где М - средний член,

(13)

Если модель имеет столько параметров, сколько ячеек, то она называется насыщенной.

Ограничения (2) имеют вид (в нашем случае):

; ;

введены упрощения и просуммируем обе части (1) по I, AB

(14)

с учетом (2) будем иметь:

(15)

Суммируя по всем наблюдениям, получим:

(16)

Следовательно, M=v, подставляя это в (3), мы найдем:

(17)

С помощью (4) можно интерпретировать Х как добавку (или убыль), связанную с категорией фактора А по сравнению с общим средним. Дополнительный свет на уравнение (4), применительно к таблицам:

; ;

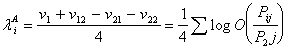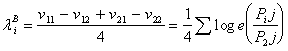(18)

.

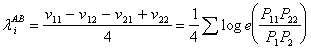Выше была рассмотрена двумерная модель или таблица с двумя входами, а нам необходимо определить порядок действия в случае многомерных таблиц.

Задача состоит в том, чтобы выбрать из всего многообразия одну или несколько относительно простых моделей.

Используем насыщенную модель. При подборе насыщенной модели оценивалась значение всех , какие только можно себе представить включенными в подходящую простую модель. Некоторые из значений могут оказаться близкими к 0, что будет указывать на их малую вероятность. Тогда при выборе ненасыщенной модели можно руководствоваться стремлением включить в нее, прежде всего, те , которые существенно отличаются от 0.

При построении ненасыщенной модели использовались два простых метода:

а) метод включения, который заключается в том, что на каждом шаге в модель вводится наиболее важный

б) метод исключения, суть которого в том, что на каждом шаге из модели исключается наименее важный .

Введение дополнительного параметра в модель может привести к ее улучшению. Один из методов или какая-нибудь их комбинация обязательно приведут к единственной наилучшей модели.

Программное обеспечение задачи. Для реализации описанных алгоритмов задачи используется пакет прикладных программ задач SAS-82,4. Для обработки данных и моделирования использовалась процедура EUNCAT, обрабатывающая категориальные переменные.

В каждом уравнении на первом этапе используется процедура без дополнительной опции, а на последнем этапе с опциями FRF Q,X, PREDICT. Итак, в работе:

1. Предложены методы обработки и анализа материалов исследований.

2. Разработаны математико-статистические модели влияния состояния окружающей среды на заболеваемость населения.

ЛИТЕРАТУРА

1. Никитин Д.П. Новиков Ю.В. Окружающая среда и человек. -М.: 1980.-320 с.

2. Алексеев С. Чрезвычайные ситуации на производстве // Нефтяное хозяйство.-2000. -№ 3. С. 12-16.

3. Солтаганов В., Щегорцов В. Трубопроводы сквозь призму национальной безопасности// Нефть Росси.-2003.-№ 1.-с.105-107.

4. Айдосов А., Тургамбаева К.С. Моделирование распространения вредных веществ в пограничном слое атмосферы нефтегазоконденсат добывающих регионов // Гидрометеорология и экология.-2002.-№ 2.-с.21-31.

5. Айдосов А. Комбинированная модель расчета концентрации от нестационарного непрерывного источника// Гидрометеорология и экология. Алматы, 2002.-№ 3.-с.7-15.

6. Коровкин И.А. Пашков Е.В. Система экологического управления как основа стандартов//Стандарты и качество.-1997.-№6.-С.12-18.