Дуйшеналиев Т.Б., Сарсенов Б.Т.

КГТУ им. И. Раззакова, Бишкек, Кыргызстан

О ДИНАМИКЕ НАЗЕМНОГО СООРУЖЕНИЯ В ЭПИЦЕНТРЕ ЗЕМЛЕТРЯСЕНИЯ И ВДАЛИ ОТ НЕГО

Для решения нестационарных задач в упругих средах одним из наиболее удобных в приложениях методов является метод бихарактеристик с использованием идей метода расщепления, развитый Г.Т. Тарабриным [1]. В настоящей работе используется метод, развитый для решения контактных задач взаимодействия упругих тел с угловыми точками в условиях плоской деформации [2]. Принята явная разностная схема, построенная на основе метода бихарактеристик с привлечением идеи расщепления по пространственным координатам. Получены разрешающие разностные уравнения для внутренних, граничных, угловых, особых и контактных точек сопряжения полосы и полуплоскости. Для моделирования процесса сброса напряжений на трещине используются сингулярные обобщенные функции по методу, предложенному в [3].

Постановка контактной задачи. Рассмотрим составную неоднородную упругую среду: полупространство упругой однородной изотропной среды D₁ с плотностью ρ₁ и коэффициентами Ламе λ₁ и μ₁, а также упругое изотропное прямоугольное тело D₂ с высотой d₁ и шириной 2d₂, расположенное на упругом полупространстве D₁, и с плотностью ρ₂, коэффициентами Ламе λ₂, μ₂ в условиях плоской деформации при сбросе напряжений на горизонтальной трещине S, которая расположена на глубине L (x₁= L, |x₂|≤ d) (рис.1).

В начальный момент времени среда находятся в состоянии покоя

, (1)

при свободных от воздействующих нагрузок на границе полупространства и включения:

( j=1,2), при x₁ = 0, | х₂ – d₃| > d₂, (2)

s⁽²⁾_{1 j}=0 ( j=1,2), при x₁ = - d₁, | х₂ – d₃| ≤ d₂, (3)

s⁽²⁾_{2 j}=0 ( j=1,2), при | х₂ – d₃| = d₂, 0 ≤ x₁ ≤ d₁ (4)

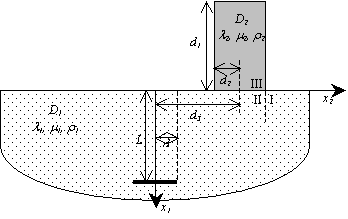
Рисунок 1 – Расчетная область

А условия на контактной границе отвечают требованиям полного сцепления :

v⁽¹⁾_i= v⁽²⁾_i, s⁽¹⁾_1j=s⁽²⁾_1j (i,j=1,2) , при x₁ = 0, | х₂ – d₃| ≤ d₂. (5)

Здесь - компоненты тензора напряжений k–ой среды, - компоненты скоростей перемещений этих сред. Так как на бесконечности отсутствуют источники колебания, то очевидным является требование, чтобы на бесконечности выполнялись условия затухания:

При описанных условиях необходимо исследовать напряженно – деформированное состояние неоднородной среды D₁ ∩ D₂ при t > 0

Определяющие уравнения. Для описания движения упругой среды используются две системы дифференциальных уравнений:

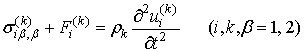, (6)

и соотношения обобщенного закона Гука:

(7)

Здесь по повторяющимся греческим индексам проводится суммирование от 1 до 2 (тензорная свертка), F^(k)_i - компоненты объемной силы.

Для моделирования сброса напряжений на трещине в полупространстве введена объемная сила, компоненты которой определяются сингулярной обобщенной функцией – простым слоем на горизонтальной трещине S [3].

Решение задачи удобно отыскивать в безразмерном пространстве переменных и искомых параметров [2].

После введения безразмерных величин, из уравнений (6), (7) после простых преобразований можно получить ( i, j, k = 1, 2):

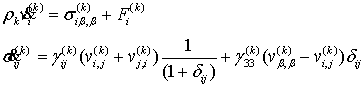(11)

Уравнения (11) представляют собой линейную неоднородную гиперболическую систему дифференциальных уравнений первого порядка с постоянными коэффициентами. Её характеристические поверхности в трехмерном пространстве (x₁; х₂; t) представляют собой конусы с осями, параллельными оси времени. Система уравнений (11) имеет два семейства характеристических конусов. Эти конусы совпадают с бихарактеристиками уравнений (11).

Процедуры получения разрешающихся разностных систем уравнений для (11) относительно неизвестных s_ij и v_i (i,j=1,2) в узловых точках A исследуемого тела в момент времени t_n+t различны для внутренних и граничных точек исследуемой области (см. [2, 4]).

Разработанная методика решения динамических задач позволяет определить скорости v_i и компоненты тензора напряжения s_{i j} в точке А на каком-нибудь слое времени t=t₀+t, если известны их значения на предыдущем слое t=t₀.

Проведены численные эксперименты по определению напряженно-деформированного состояния упругого полупространства и упругого тела при сбросе вертикальных и горизонтальных напряжений на трещине с использованием физико-механических параметров, типичных для горных пород и строительных сооружений. Построены осциллограммы скоростей перемещений дневной поверхности и упругого тела и дифракционные картины полей скоростей и напряжений при отражении и преломлении ударных волн. Исследовано влияние параметров массива, глубины трещины и характера возникающих ударных волн на напряженно-деформированное состояние среды и упругого тела. Также изучено напряженно-деформированное состояние упругого тела (сооружения) в зависимости от расстояния до эпицентра.

Литература:

1. Тарабрин Г.Т. Применение метода бихарактеристик для решения нестационарных задач динамики анизотропных массивов.// М., Строительная механика и расчет сооружений, 1981, № 4, стр. 38 – 43.

2 Джузбаев С.С., Сарсенов Б.Т. Динамическое напряженное состояние полосы при боковом импульсном давлении.// Математический журнал. Алматы. 2003. Том 3. №1(7). стр. 55 – 62

3. Алексеева Л.А., Дильдабаева И.Ш. Обобщенное решение уравнений динамики упругой среды с криволинейной трещиной при плоской деформации// Математический журнал, 2007, Т7, №2(25), стр. 19 – 31.

4. Алексеева Л.А., Сарсенов Б.Т. Модель динамики среды в окрестности очага землетрясения // Сб. научн. трудов Ниа рк. Методы экспериментальной физики. Алматы. – 2010. – С. 63-73.