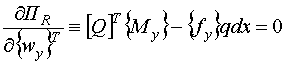К.т.н., Юшкин В.Н.

Волгоградский государственный аграрный университет, Россия

РЕАЛИЗАЦИЯ МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ В СМЕШАННОЙ ФОРМИЛИРОВКЕ ДЛЯ РАСЧЕТА ИНЖЕНЕРНЫХ СИСТЕМ

В расчетах широкое применение нашли четырехузловые конечные элементы, при формировании матриц жесткости которых используется метод перемещений [1, 2].

1. В первом варианте для расчета использован четырехузловой конечный элемент в формулировке метода перемещений. В качестве узловых неизвестных приняты перемещения и их производные. В настоящей работе выполняется сравнение алгоритмов МКЭ в формулировках метода перемещений и смешанного метода.

В качестве конечного элемента принимается произвольный фрагмент пластины с узлами i, j, k, l. Для выполнения численного интегрирования четырехугольный фрагмент отображается на квадрат с локальными координатами и . Интервалы изменения значений координат и определяются неравенствами , .

Глобальные координаты x и y произвольной точки срединной поверхности криволинейного конечного элемента связаны с локальными координатами и зависимостями:

	(1.1)

где индексами i, j, k и l отмечены величины, относящиеся к соответствующим узлам конечного элемента.

Дифференцированием (1.1) определяем производные глобальных координат в локальной системе:

	(1.2)

Производная локальных координаты в глобальной системе:

	(1.3)
,

где - .

Вектор узловых перемещений конечного элемента можно записать в локальной и глобальной системах координат:

; ,

(1.4)

где – первые производные нормального перемещения пластины в локальной и глобальной системах координат.

Перемещение произвольной точки конечного элемента и ее производная выражаются через соответствующие узловые значения в виде зависимостей:

	(1.5)
;
; .

Здесь функции – являются полиномами Эрмита третьей степени.

Для вывода матрицы жесткости и вектора сил конечного элемента используется равенство работ внутренних и внешних сил конечного элемента на возможном перемещении:

,

(1.7)

где .

2. Во втором варианте для формирования матрицы деформирования элемента в смешанной формулировке МКЭ использован модифицированный функционал Рейсснера [2, 3], который для пластины можно представить выражением:

(2.1)

где – момент в рассматриваемом сечении;

; S – площадь пластинки.

Здесь принято

.

(2.2)

Для получения матрицы деформирования конечного элемента использованы следующие интерполяционные зависимости:

; ; ,

(2.3)

где ; ;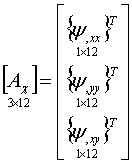

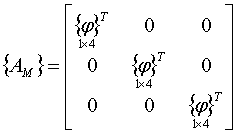– билинейные функции формы;

С учетом аппроксимирующих выражений функционал (2.1) запишем в виде:

,

(2.4)

где – матрица преобразования узловых неизвестных из локальной системы координат в глобальную.

Минимизируя равенство (2.2), можно записать следующие матричные зависимости:

; ,

(2.5)

где , , .

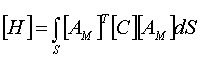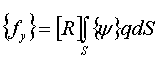Уравнение (2.3) можно записать в матричном виде:

,

(2.6)

где

, , .

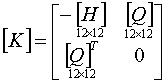В качестве примера была рассмотрена консольная балка, находящаяся под действием равномерно распределенной нагрузки интенсивности . Моменты в заделке оказались в обоих вариантах расчета одинаковыми при представлении балки одним элементом.

Литература

1. Николаев А.П., Клочков Ю.В., Киселев А.П., Гуреева Н.А. Векторная интерполяция перемещений в конечно-элементных расчетах оболочек. – Волгоград, 2012. – 262 с.

2. Галагер Р. Метод конечных элементов. Основы. Пер. с англ. – М.: Мир, 1984. – 428 с.

3. Гуреева Н.А. Гибридных четырехугольный элемент осесимметрично нагруженного тела вращения с неизвестными перемещениями и напряжениями в узлах // Изв. вузов Северо-Кавказский регион. Серия: Технические науки, 2007, №1, с. 31-33.
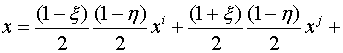
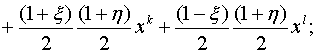
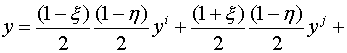
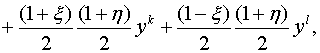
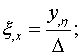
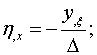
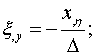
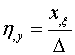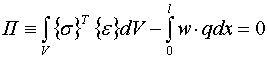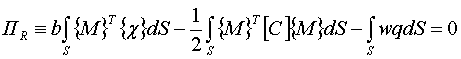
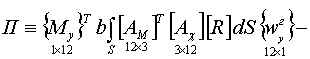
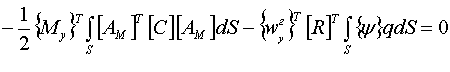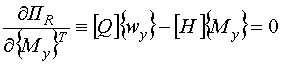