Технические науки/ 2.Механика
Ольховская Е.П.,
Давыденко М.В.
ГБПОУ Краснодарского
края «Пашковский сельскохозяйственный колледж»
Гармония хаоса и порядка. Построение примера механической
самоорганизующейся системы.
Все системы в природе стремятся к равновесию.
Однако, если исключить часто встречающийся, но неинтересный крайний случай
безразличного равновесия - раскрученная пружина, упавший камень, то придется
признать: это стремление систем постоянно остается неудовлетворенным - огромное большинство состояний неравновесны.
А это значит, что, достигнув равновесия, система переходит от большего числа
состояний к меньшему. То есть она совершает выбор в том смысле, что некоторые
состояния ею отвергаются - те, что она покидает, а некоторые сохраняются - те,
в которые она переходит.
Целью данной работы стало желание ознакомить
окружающих с понятием синергетики заставить задуматься над вопросом «А все ли
на свете происходит хаотично?», а также продемонстрировать пример механической
самоорганизующейся системы. Авторы выдвигают гипотезу о том, что все процессы в
жизни, природе, технике происходят не случайно.
Основы синергетики. Синергетика (это понятие
означает кооперативность, сотрудничество, взаимодействие различных элементов
системы) -по определению ее создателя Г. Хакена - занимается изучением систем,
состоящих из многих подсистем самой различной природы, таких как электроны,
атомы, молекулы, клетки, нейтроны, механические элементы, фотоны, органы
животных и даже люди... Это наука о самоорганизации простых систем, о
превращении хаоса в порядок.
Объект изучения синергетики, независимо от его
природы, обязан удовлетворять следующим требованиям: 1) открытость -
обязательный обмен энергией и (или) веществом с окружающей средой; 2)
существенная неравновесность - достигается при определенных состояниях и при
определенных значениях параметров, характеризующих систему, которые переводят
ее в критическое состояние, сопровождаемое потерей устойчивости;
3)
выход из критического состояния скачком, в процессе типа фазового перехода, в
качественно новое состояние с более высоким уровнем упорядоченности.
Самоорганизующиеся системы обретают присущие им
структуры или функции без какого бы то ни было вмешательства извне. Обычно эти
системы состоят из большого числа подсистем. При изменении определенных
условий, которые называются управляющими параметрами, в системе образуются
качественно новые структуры. Эти системы обладают способностью переходить из
однородного, недифференцированного состояния покоя в неоднородное, но хорошо
упорядоченное состояние или в одно из нескольких возможных состояний.
Самоорганизующиеся системы способны сохранять внутреннюю
устойчивость при воздействии внешней среды, они находят способы самосохранения,
чтобы не разрушаться и даже улучшать свою структуру.
Примеры самоорганизующихся систем.
Под открытыми системами понимают термодинамические
системы, которые обмениваются с окружающей средой веществом и энергией. К
открытым системам относятся биологические системы - живые организмы, также
обменивающиеся веществом и энергией с окружающей средой. В отличие от замкнутых
систем, в которых энтропия возрастает и стремится к равновесному максимальному
значению, в открытых системах возможны стационарные неравновесные состояния с
постоянной энтропией, при которых хотя и происходит производство энтропии,
однако она непрерывно отводится за пределы системы. В стационарных состояниях
стационарное значение энтропии не соответствует ее максимуму, в отличие от
замкнутых систем. Оказывается, что если в открытых системах происходят
нелинейные процессы, то в таких системах могут осуществляться термодинамически
устойчивые, в частном случае стационарные состояния, далекие от
термодинамического равновесия и характеризующиеся определенной пространственной
и/или временной упорядоченностью, т.е. структурой. Такие структуры называют
диссипативными, поскольку для их существования требуется непрерывный обмен
веществом и энергией с окружающей средой, т.е. диссипация (рассеяние) энергии.
Приведем некоторые примеры самоорганизации материи в открытых системах.
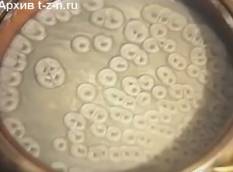
 Ячейки Бенара. Для поддержания ячеистой структуры в
жидкости требуется подвод (снизу) и отвод (сверху) тепла. Другим примером из
гидродинамики является возникновение тороидальных вихрей Тейлора между
вращающимися цилиндрами.
Ячейки Бенара. Для поддержания ячеистой структуры в
жидкости требуется подвод (снизу) и отвод (сверху) тепла. Другим примером из
гидродинамики является возникновение тороидальных вихрей Тейлора между
вращающимися цилиндрами.
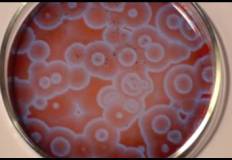
![[]](./2_172818.doc.files/image008.jpg) Реакция Белоусова-Жаботинского. В химии примером
является реакция Белоусова-Жаботинского, представляющая собой периодическую
химическую реакцию, сопровождающуюся периодическим изменением цвета реакционной
смеси. Эту пульсирующую реакцию еще называют химическим маятником. Указанные
химические процессы и реакции лежат в основе жизни.
Реакция Белоусова-Жаботинского. В химии примером
является реакция Белоусова-Жаботинского, представляющая собой периодическую
химическую реакцию, сопровождающуюся периодическим изменением цвета реакционной
смеси. Эту пульсирующую реакцию еще называют химическим маятником. Указанные
химические процессы и реакции лежат в основе жизни.
Биологические примеры. В биологии примерами являются все живые организмы. Живой
организм - это устойчивая саморегулирующаяся открытая система, обладающая
высокой организацией на молекулярном и на макроскопическом уровне, в которой
протекают нелинейные химические реакции. Поэтому теория открытых систем
представляет особый интерес для исследования физико-химических процессов,
лежащих в основе жизни; в экологии
примером является организация сообществ, в частности возникновение
периодической во времени численности особей жертвы и хищника. Такая
диссипативная структура поддерживает существование за счет поступления
растительного питания для жертв и организованного отлова хищников; на
общебиологическом, экологическом уровнях важнейшей диссипативной структурой
является биосфера Земли, как целостная согласованно функционирующая система,
получающая энергию, в основном, от Солнца усваивающая ее в растениях и
переизлучающая тепло в космическое пространство. Из всей достигающей
поверхности Земли солнечной энергии лишь незначительный процент расходуется на
фотосинтез, и этой доли энергии достаточно для обеспечения всего живого
вещества планеты и поддержания его состояния с низкой энтропией;
Построение механической самоорганизующейся
системы. В качестве примера механической самоорганизующейся системы
была выбрана установка, состоящая из 15 математических маятников. Маятники
подвешены на нитях длиной от 21,2 до 34,4 см, которые были вычислены с помощью
формулы периода математического маятника в электронных таблицах EXСEL. Самый длинный
совершает 51 колебание в минуту, самый короткий 65.
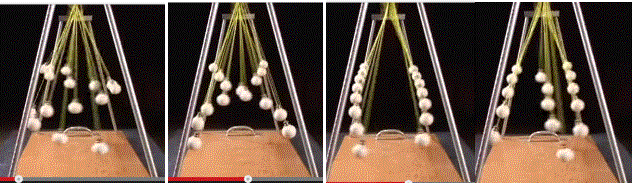 0Приведем несколько фотографий процесса движения совокупности
математических маятников. На них видно, что сначала шарики выстраиваются в одну
волну, затем разбиваются на 3 и 2 волны, в промежутках, шарики выстраиваются в
2 и 3 шеренги. Затем снова все возвращается к 1 волне.
0Приведем несколько фотографий процесса движения совокупности
математических маятников. На них видно, что сначала шарики выстраиваются в одну
волну, затем разбиваются на 3 и 2 волны, в промежутках, шарики выстраиваются в
2 и 3 шеренги. Затем снова все возвращается к 1 волне.
Данная система полностью удовлетворяет всем параметрам, необходимым для
названия ее именно самоорганизующейся. Актуальность и практическая ценность данной
установки заключается в следующем: можно и нужно использовать как наглядную
демонстрацию зависимости периода колебаний от длины подвеса; на дополнительных,
факультативных, кружковых занятиях по физике; на занятиях по естествознанию у
студентов специальностей нетехнического профиля; в качестве наглядного примера системы, члены которой не зависимы
друг от друга, а в процессе движения организуют четкие структуры, на занятиях
по философии, политологии; для
популяризации науки, представления на конференциях и семинарах.
ЛИТЕРАТУРА
1. Самоорганизующиеся системы, пер. с англ. М., 1964;
2. Принципы самоорганизации, пер. с англ. М., 1966;
3. Эйген М., Винклер Р. Игра жизни, пер. с нем. М., 1979;
4. Николис Г., Пригожин И. Самоорганизация в неравновесных системах, пер. с
англ. М., 1979;
5. Пригожин И. От существующего к возникающему, пер. с англ. М., 1985;