Технические науки/8. Обработка материалов в машиностроении

Д.т.н. Бржозовский Б.М., д.т.н. Янкин И.Н.

Саратовский государственный технический университет

им. Гагарина Ю.А., Россия

Оптимизация режима обработки по составу колебательного процесса в зоне резания

Процесс резания на металлорежущих станках протекает в условиях интенсивного упруго-пластического деформирования обрабатываемого материала, что сопровождается значительным возмущающим воздействием на упругую систему станка. Следствием такого возмущения является образование колебаний в формообразующих подсистемах резания. Колебания протекают непосредственно в зоне формообразования обрабатываемой поверхности, поэтому их влияние оказывается значимым как при формировании точности ее формы, так и ее микрогеометрических параметров. Вместе с тем, при назначении режима обработки вступают в противоречие два основных фактора. С одной стороны имеет место стремление назначить режим, обеспечивающий максимальную скорость съема материала. С другой стороны, необходимо исключить возможность выхода динамической системы резания за пределы ее устойчивости, поскольку в таких условиях развиваются колебания на собственных частотах системы резания и снижается качество обработки.

Признаком устойчивого и стабильного резания является стохастический вид колебательного процесса, который генерируется в зоне резания. Возникновение неустойчивости динамической системы резания проявляется в образовании неслучайной или детерминированной составляющей в колебательном процессе. Появление неслучайных составляющих является сигналом к тому, что динамическая система резания входит в неустойчивую область функционирования.

Рассмотрим алгоритм получения информации из сигнала колебательного процесса.

Первый этап. Осуществляем запись порции оцифрованного сигнала из зоны резания. С этой целью можно использовать хорошо зарекомендовавшие себя пьезоэлектрические измерительные преобразователи. Реализация оцифрованного сигнала колебаний описывается массивом ординат x₁…x_n на временном отрезке T=n×Dt, где Dt – период дискретизации; n – число точек в реализации сигнала.

Второй этап. Применение классического спектрального преобразования дает массивы коэффициентов Фурье:

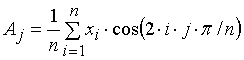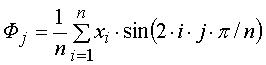; , , (1)

где обозначено: i – порядковый номер точки в реализации колебательного процесса; j – номер гармоники. Полученные массивы коэффициентов дают возможность получить спектр колебаний S(j) в диапазоне гармоник j_н..j_к. Здесь верхняя граница гармоник j_в устанавливается в соответствии с частотными характеристиками системы измерения или по результатам опытных данных. Нижняя граница j_н вводится с целью повышения достоверности информации путем исключения влияния на результаты вынужденных колебаний станка на частотах его вращающихся элементов.

Третий этап. С целью получения массивов скорости V и смещения S, необходимых для получения фазовой картины колебательного процесса, выполняем их расчет по выражениям:

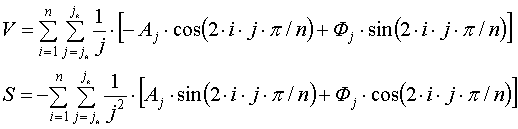. (2)

Четвертый этап. Рассчитываем коэффициент корреляции K_vs между спектрами скорости S_v и смещения S_s, получаемых на основе массивов V и S. Если K_vs<K_гр, то выполняем фильтрацию несущественных гармоник спектра S(j), приняв , для гармоник спектра с амплитудой, удовлетворяющих условию:

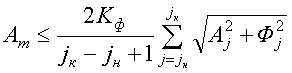, (3)

где K_ф - коэффициент фильтра (). Практические данные, полученные для различных видов обработки, показали, что границу фильтрации целесообразно ограничить величиной K_гр=0,97. Процесс наращивания уровня фильтрации K_ф повторяем до тех пор, пока не будет достигнут K_гр. Тогда доля неслучайной составляющей может быть оценена коэффициентом K_д=1- K_ф.

В качестве примера рассмотрим реализацию способа фазовых диаграмм для условий точения и растачивания отверстия на одном и том же токарном станке.

На рис. 1 показаны фрагменты алгоритма выделения неслучайной составляющей в порции сигнала колебания на операции точения. В левой части помещены макет исходного сигнала, спектры сигналов скорости V и смещения S, рассчитанные в диапазоне частот 0,1-5 кГц. В правой части рисунка расположена фазовая диаграмма в системе «смещение S – скорость V». Коэффициент неслучайной составляющей на операции точения получен на уровне K_д=0,64.

Аналогичный алгоритм применен для сигнала, записанного на операции растачивания. Результат представлен на рис. 2, где коэффициент неслучайной составляющей достигает уровня K_д=0,97. Как видно, при обработке на одном и том же станке разными инструментами наблюдается существенное изменение состава колебательного процесса. Такое различие при точении и растачивании объясняется существенным изменением характеристик динамической системы резания за счет использования консольного инструмента. При точении неслучайные формы колебаний проявляются в диапазоне частот 2,25-2,6 кГц, а при растачивании система резания имеет высокую склонность к образованию детерминированной вибрации на частоте 1,2 кГц, о чем свидетельствует высокая плотность и степень повторяемости траекторий фазовой диаграммы.

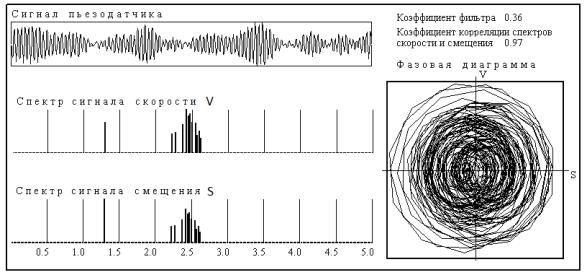
Рис. 1. Фазовая диаграмма сигнала при точении

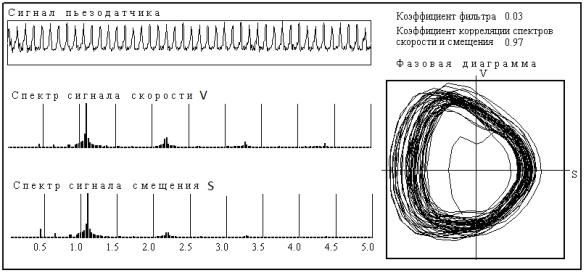
Рис. 2. Фазовая диаграмма сигнала при растачивании

Рассмотрим пример поиска оптимального режима обработки. С этой целью выполнен эксперимент путем обтачивания детали при варьированиях частоты вращения шпинделя от 125 до 800 мин^-1, продольной подачи от 0,07 до 0,14 мм/об при глубинах резания 1 и 2 мм. Число вариантов обработки n=6_V·4_S·2_T=48. При резании осуществлялась регистрация сигнала колебаний с пьезоэлектрических датчиков, установленных на суппорте станка с последующей оцифровкой и обработкой сигнала по описанному выше алгоритму с применением статистической обработки результатов.

а	б

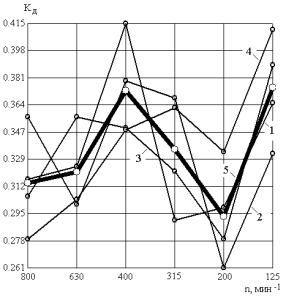
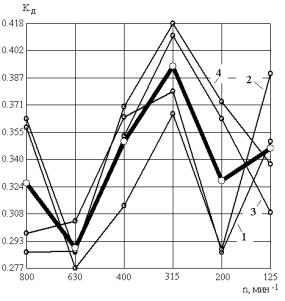
Рис. 3. Влияние режима обработки на состав колебательного процесса при глубине резания t=1мм (а) и t=2мм (б):

1 – S_пр=0,07 мм/об; 2 – S_пр=0,084 мм/об; 3 – S_пр=0,11 мм/об;

4 – S_пр=0,14 мм/об; 5 – усредненная кривая по четырем подачам

На рис. 3 приведены результаты обработки сигналов колебаний. Доля детерминированной составляющей представлена коэффициентом K_д, который рассчитывался по двадцати реализациям колебаний с периодическим движением начала отсчета по файлу колебаний и последующей статистической обработкой. Как видно, на соотношение стохастических и неслучайных составляющих в колебательном процессе существенное влияние оказывает частота вращения шпинделя. Причем, если при глубине резания t=1 мм (рис. 3а) наблюдается значительный разброс форм кривых 1-4, отражающих влияние частоты вращения шпинделя на K_д при изменении продольной подачи от 0,07 до 0,14 мм/об, то при глубине резания t=2 мм между подобными кривыми отмечается более высокая корреляция (рис. 3б). Экстремальное значение частоты вращения шпинделя составляет 400 мин^-1, при которой в колебательном процессе возрастает доля неслучайной составляющей и на которой нерационально вести обработку. С другой стороны, если необходимо минимизировать детерминированную вибрацию, то частоты вращения 630 и 200 мин^-1 являются наиболее предпочтительными.

Как показали результаты исследования, процесс стружкообразования, реализуемый через сложные нелинейные процессы упруго-пластического деформирования и разрушения обрабатываемого материала, чувствителен к сочетанию динамических характеристик станка и скоростных характеристик движения режущего клина в обрабатываемом материале. Разные сочетания указанных факторов дают различную картину колебательного процесса. В этой связи, изложенный выше способ оценивания состава колебательного процесса при механической обработке целесообразно использовать для поиска оптимального режима резания. Кроме того, применение способа оценивания состава колебательного процесса в системах диагностирования технологического оборудования в качестве источника информации о состоянии рабочих процессов и в других технических системах, где требуется высокая информативность о протекающих в них динамических процессах.