Калинина М.Ф.

Национальный технический университет Украины «КПИ»

СТРУНА С ДВУМЯ ЗАКРЕПЛЕННЫМИ КОНЦАМИ

Аналитическое описание упругого взаимодействия акустических полей с механическими системами в самой общей постановке не может быть реализовано, принимая во внимание чисто математические трудности построения такой модели. Детальное описание структуры процесса с получением решения в элементарных функциях, конечно можно реализовать, но, как показывает практика подобных исследований, чтобы иметь представление о характере явления с достаточной степенью достоверности, можно ограничиться изучением приближенных (имитационных) моделей.

Вместе с тем, расширяя круг задач, используя ПЭВМ, можно одновременно выполнять системный анализ для возмущающих факторов различной физической природы, и углублять, обобщать и расширять уже известные методы асимптотического и более точного описаний.

В качестве первого приближения математической модели торсиона рассмотрим, так называемое, волновое уравнение. С помощью этого уравнения, описываются поперечные колебания струн, продольные колебания стержней, плоские звуковые колебания и т.д.

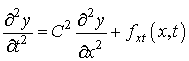, (1)

где – параметр, который исследуется и представляет собой поперечное отклонение точки струны (рис. 1); – время; – пространственная координата, ; – геометрический размер; – коэффициент (скорость распространения волн вдоль оси ); – внешняя сила,.

Исходное состояние струны, как это вытекает из уравнения (1), должно задаваться в виде начальной формы и начальных скоростей всех точек струны:

; (2) (3)

Начальные условия представим в виде двух независимых подпрограмм-функций на Турбо-Паскале, заголовки которых будут иметь вид

function YN(х:real):real; function DYN(х:real):real.

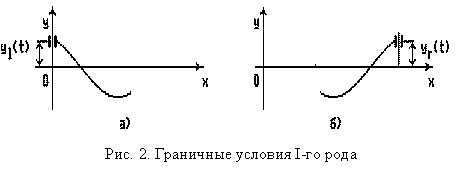
Конкретный вид каждой из этих функций будет определяться особенностями задачи, которая решается. Граничные условия на концах струны будем считать принадлежащими одному из трех типов (I, II или III рода). Для левого конца струны граничное условие I рода (NGL=1, рис. 2, а) предполагает выполнение равенства в виде закона перемещения левого конца струны во времени (условие Дирихле).

(4)

Граничное условие II рода, условие Неймана (NGL=2, рис. 3, а)

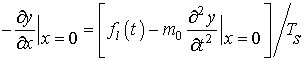(5)

задает поперечную силу , которая приложена к левому концу струны. В уравнении (5), кроме того, учтена сила инерции груза массы , закрепленного на левом конце струны (левый конец с грузом может скользить вдоль направляющей, ось которой совпадает с осью ). – здесь обозначает натяжение струны.

Граничное условие III рода – условие Робена (NGL=3,) задает перемещение

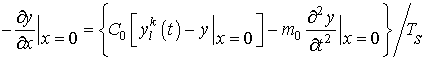(6)

точки, которая связана с левым концом пружиной жесткости . Здесь, как и при условии (5), левый конец считается связанным с массой , которая скользит вдоль направляющей, т.е. вдоль оси .

Аналогично для правого конца струны . Граничное условие

I рода (NGR=1, рис. 2, б) -

; (7)

II рода (NGR=2) -

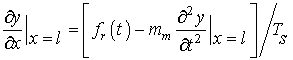; (8)

III рода (NGR=3,) –

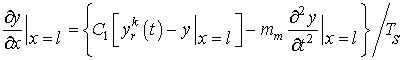. (9)

Начальное положение массы совпадает с положением соответствующей точки струны. Начальную скорость этой точки задаем подпрограммой-функцией с заголовком –

Function Dyg :real.

Значение этой функции зависит от варианта Nvr.