Калинина М.Ф.

Национальный технический университет Украины «КПИ»

ОПРЕДЕЛЕНИЕ ПЕРЕДАТОЧНОЙ ФУНКЦИИ СТРУННОГО ПОДВЕСА ПО ЕГО ДИСКРЕТНО-НЕПРЕРЫВНОЙ МОДЕЛИ

Математическая модель струнного подвеса в виде волнового уравнения, в первом приближении достаточно полно описывает особенности динамики упруго-напряженного состояния. Для раскрытия более тонких моментов эксплуатационного функционирования, струнный подвес следует рассматривать в виде тяжелой нити, нагруженной одним грузом на свободном конце, либо несколькими по всей протяженности.

Два последних варианта могут быть описаны одним уравнением

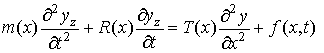. (1)

Здесь x, t – линейный размер и время, y – отклонение точки подвеса от положения ее равновесия; m(x), R(x), T(x) – соответственно масса, коэффициент сопротивления и натяжение нити.

В волновом уравнении натяжение принимается постоянным. В случае тяжелой нити, натяжение в каждой точке равно сумме масс сосредоточенных под данной точкой помноженной на ускорение земного тяготения g. Внешняя поперечная сила обозначена через .

Точные решения уравнения (1) известны, но они крайне громоздки для использования в инженерных расчетах. Поэтому представляет практический интерес поиск такой приближенной модели, которая, не в ущерб объективности картины явления, была бы менее трудоемкой. Такой математической моделью может быть дробно-рациональная модель струны.

Динамическую модель подвеса в этом случае представим как совокупность сосредоточенных масс, соединенных между собой нерастяжимыми нитями. Расстояние между соседними массами h=l/m считаем неизменным (здесь l – длина струны, m – количество отрезков, на концах которых сосредоточены массы).

Массу нити равномерно распределяем между сосредоточенными массами (m_z=m_стр/m; 1 < z < m-1; m_z – сосредоточенная масса, m_стр – масса струны). Сосредоточенным массам и на концах струны придаем массу . В этом случае общая масса струны будет равна сумме сосредоточенных масс. Если на струне фиксируется произвольное число сосредоточенных масс любой величины, тогда их массы складываются с сосредоточенными массами. Окончательное распределение масс между сосредоточенными точками фиксируется массивом Mb:Coef (type Coef=array[-1..30] of real).

	-1	0	1	2	3	...	m	...	30
Mb	m	m0	m1	m2	m3	...	mm

Силы сопротивления перемещениям воспроизводятся массивом Mr той же структуры, что и массив Mb. На z-ю сосредоточенную массу действует сила, которая равна силе сопротивления, приложенной к отрезку длины h. Если же на струне фиксированы массы с ненулевыми размерами, тогда сопротивление, обусловленное наличием этих масс, отображается соответствующим увеличением элементов массива Mr.

Массив T:Coef заполняется значениями натяжения (постоянная для модели струны).

Дискретная модель струнного подвеса приобретает вид –

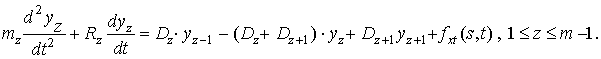(2)

Здесь введено обозначение . В последующем используем массив D:Coef.

Граничные условия будем рассматривать трех родов: Ngl=1,2,3 для x=0; Ngr=1,2,3 для x=l.

Для левого конца (x=0)

, (3)

где – перемещение точки x=0 подвеса.

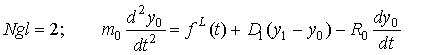, (4)

здесь – сила, приложенная в точке x=0.

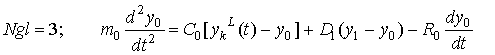, (5)

где С₀ – коэффициент жесткости пружины, один конец которой соединен с подвесом в т. x=0, а другой перемещается на величину .

Для правого конца (x=)

, (6)

где – перемещение точки x=l подвеса.

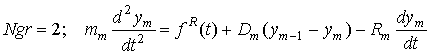, (7)

где – сила, действующая на точку x=l.

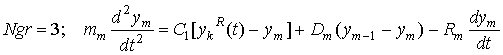, (8)

где С₁ – жесткость пружины, один конец которой соединен со струной в т. x=l, а другой перемещается на величину .

Поскольку математическая модель формируется для определения передаточной функции произвольного канала, постольку для выбранного канала возмущающее воздействие (входной сигнал) считается присутствующим, все другие принимаются равными нулю.