Экономические науки/8. Математические методы в экономике

К.э.н. Копытина М.Л.

Воронежский государственный аграрный университет имени К.Д. Глинки, Россия

Простая ставка дисконтирования и простая внутренняя норма доходности (SIRR- Simple Internal Rate of Return).

В данной работе под инвестиционным проектом понимается детерминированная последовательность чисел , отражающая последовательные финансовые результаты: плановые, расчетные, прогнозные или прошлые. Числовые же характеристики проекта (функционалы, заданные на последовательности чисел ) могут использовать различные ставки депозитов, ставки дисконта, предположения о возможной степени изменчивости показателей .

За k периодов времени показатель наращивания доходов составит при начислении простых процентов величину (1+kr).

Определение 1. Поток финансовых платежей назовем стандартным потоком первого рода А или стандартным потоком кредитора, если он имеет следующий вид: , где . Стандартный поток первого рода является частным случаем регулярного потока (см. определение в [1].)

Определение 2. Простой внутренней нормой доходности постнумерандо стандартного проекта первого рода SIRR определим как величину показателя являющегося корнем уравнения

(1)

Чистый доход проекта предполагается положительным и равным

>0; (2)

Чистый простой дисконтированный доход проекта определим по формуле

(3)

Чистый простой наращенный доход проекта определим по формуле

(4)

Предельный чистый простой наращенный доход равен

(5)

Из формулы (2) вытекает формула расчета простой внутренней нормы доходности

SIRR=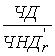 . (6)

Хорошо известна формула средневзвешенной стоимости капитала (Weighted Average Cost of Capital, WACC), которая является показателем, характеризующим стоимость капитала так же, как ставка банковского процента характеризует стоимость привлечения кредита. WACC широко используется в инвестиционном анализе, его значение используется для дисконтирования ожидаемых доходов от инвестиций, расчета окупаемости проектов, в оценке бизнеса и других приложениях. Дисконтирование будущих денежных потоков со ставкой, равной WACC, характеризует обесценивание будущих доходов с точки зрения конкретного инвестора и с учетом его требований к доходности инвестированного капитала. Расчет ставки дисконта (WACC)

WACC = We *Ke + Wd *Kd (7)

где: We- вес акционерного капитала в общей капитализации; cовокупная рыночная стоимость обыкновенных и привилегированных акций Ke- стоимость акционерного капитала. Wd - вес долга в общей капитализации; Kd- стоимость долга. В данной формуле не учитывается экономия на налоговых расходах, возникающая при выплате процентов по кредиту («налоговый щит»).

Использование WACC в качестве ставки дисконтирования было бы теоретически оправдано, если бы для IRR или для SIRR доходности было бы справедливо равенство типа (7). К сожалению, такой формулы доказать не удается, за исключением простейших однопериодных инвестиционных проектов. В данном пункте мы получим формулу позволяющую оценивать простую внутреннюю норму доходности суммарного проекта через нормы доходности его составляющих. Для обычной нормы доходности такой формулы взвешенной через нормы доходности составляющих для суммы проектов вообще не существует. В этом случае можно только показать, что норма суммарного проекта не меньше минимальной и не больше максимальной нормы доходности (свойство усредняемости).

Пусть имеется два инвестиционных проекта вида: A= и

B= . Тогда проект вида = назовем суммой проектов А и B.

Утверждение. Справедливо следующее соотношение:

SIRR ()=μ SIRR ()+(1- μ) SIRR (), где 0<μ<1. (8)

Доказательство. Очевидно, что

и .

Следовательно,

SIRR ()===

=+.

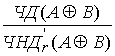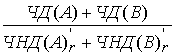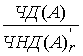
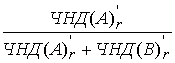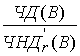
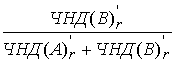Обозначим μ=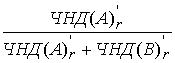. Тогда формула (8) следует из равенства:

SIRR ()= 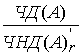μ +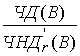 (1-μ)= μ SIRR ()+(1- μ) SIRR ().

Что и требовалось. Приведем сравнительные примеры расчетов SIRR и обычной IRR. Результаты расчетов сведем в таблицу 1.

Таблица 1

Результаты расчетов SIRR и IRR.

Исходные данные по периодам				SIRR	IRR
-270	170	170	170	0,8	0,179
-330	50	50	350	0,143	0,077
-330	350	50	50	0,5	0,162

Как видно из таблицы 1, SIRR для проектов первого рода значительно превышает по величине обычный показатель IRR. И этот факт нужно учитывать при определении эффективности проекта. Однако простая внутренняя норма доходности обладает и замечательным свойством. Для сложных проектов она, как правило, всегда существует. Это вытекает из формулы (6). SIRR не существует при единственном сочетании параметров проекта, а именно, при

=0.

Приведем пример в таблице 2, когда не существует обычной положительной IRR, но легко вычисляется SIRR.

Таблица 2.

Примеры проектов с положительным SIRR и отрицательным IRR.

Исходные данные по периодам				SIRR	IRR
-330	350	50	-50	0,083	- 0,064
-330	50	50	2 50	0,024	-0,021

Наконец, отметим, что в отличие от обычного IRR решение задачи по нахождению SIRR, если оно существует, всегда единственное. Этот факт также следует из формулы (6).

Литература:

1. Виленский П.Л., Смоляк С.А Показатель внутренней нормы доходности проекта и его модификации // Аудит и финансовый анализ. – 1999. №4.