Экономические науки/8. Математические методы в экономике

К.п.н. Савина А.Г

Орловский государственный институт экономики и торговли, Россия

Использование аппарата теории дифференциальных уравнений при моделировании инфляционных ожиданий населения

Социально-экономические исследования показали, что на экономические процессы в условиях инфляции заметное влияние может оказывать настроение основной части населения относительно ожидаемого в будущем темпа роста цен. Так, если большая часть населения страны ожидает дальнейшего усиления роста цен, она не станет вкладывать сбережения в банки, а будет покупать впрок товары повседневного спроса, менять деньги на твердую валюту, т.е. будет вести себя экономически разумно, и в результате темпы роста цен действительно будут увеличиваться.

Если же основная доля населения полагает, что в ближайшем будущем будет оживление в экономике и темпы инфляции снизятся, то люди будут больше покупать товаров длительного пользования и вкладывать деньги в
банки (и, тем самым, инвестировать экономику страны), в результате, как правило, такое оживление в экономике действительно наступает.

Описанное выше явление называется инфляционным ожиданием и
играет заметную роль в макроэкономических теориях и в социальной психологии населения.

Для количественного описания этого явления может быть использовано дифференциальное уравнение вида

, (1)

где E=E(t) - ожидаемый населением темп роста цен в момент времени t ,

R(t) - фактический темп роста цен в момент времени t,

b > 0 - коэффициент адаптации населения к изменениям темпа инфляции.

Смысл уравнения (1) в следующем: скорость изменения ожидаемого темпа роста цен во времени прямо пропорциональна ошибке инфляционного ожидания, т.е. разности между ожидаемым E и фактическим R темпами роста цен, и имеет знак, обратный этой разности.

Дифференциальное уравнение (1) описывает широко распространенный тип процессов, называемых процессами выравнивания, с которыми часто сталкиваются при описании различных физических явлений, например, процесс остывания нагретого тела до температуры окружающей его среды.

Выполняя элементарные алгебраические преобразования, мы убеждаемся, что уравнение (1) представляет собой линейное неоднородное дифференциальное уравнение первого порядка

, ( 2 )

где - неизвестная нам функция инфляционных ожиданий населения,

R(t) - заданная нам функция фактического темпа роста цен.

Используя один из стандартных алгоритмов, найдем общее решение неоднородного д.у. (6), определим частные решения этого д.у. при некоторых характерных начальных условиях и дадим экономическую интерпретацию полученным решениям.

Рассмотрим анализ общего решения уравнения (2)

(3)

при некоторых типах функции R(t) и начальных условиях E(0)=E₀ .

Случай 1. Пусть ,т.е. в момент времени t=0 произошел инфляционный скачок, а далее темп роста цен остается постоянным во времени. Тогда

откуда общее решение д.у. (3) имеет вид

( 4 )

Здесь представляет интерес рассмотреть два варианта начальных условий.

Вариант 1. Пусть E(0) = E₀ (*) , где E₀ < R₀ .

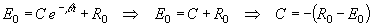Подставляя (*) в ( 4 ), находим

(**)

Подставляя (**) в (4) получим искомое частное решение д.у. (2)

( 5 )

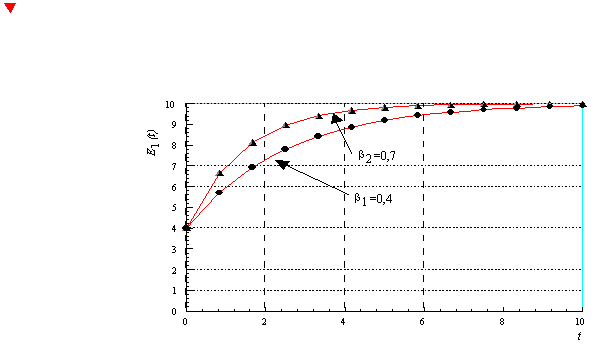Эта ситуация характерна для адаптации населения к резкому одноразовому инфляционному скачку со следующей стабилизацией величины темпа роста цен. Поскольку фактический темп роста цен R₀ в момент t = 0 оказался выше ожидаемой населением величины E₀, то инфляционные ожидания населения будут монотонно возрастать во времени t асимптотически приближаясь к фактическому уровню R₀ = const (Рис.1).

Рис.1 Графики функции E₁(t) для R₀ =10, E₀ = 6, b₁= 0,4 , b₂= 0,7.

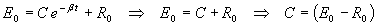Вариант 2. Пусть E(0) = E₀ (*) , где E₀ > R₀ . Тогда при подстановке (*) в ( 4 ) имеем

(**)

Подставляя (**) в ( 4 ) , имеем

(6)

Функция (6) описывает адаптацию населения к скачкообразному снижению темпа роста цен с последующей его стабилизацией во времени. Если фактически темп роста цен R₀ оказался ниже ожидаемого населением величины E₀ , то инфляционные ожидания населения будут монотонно ( по экспоненте) снижаться и асимптотически стремиться к фактическому уровню R₀ = const (Рис.2). В уравнениях (5) и (6) величина b характеризует скорость адаптации населения к новым экономическим условиям: чем больше b, тем быстрее происходит адаптация.

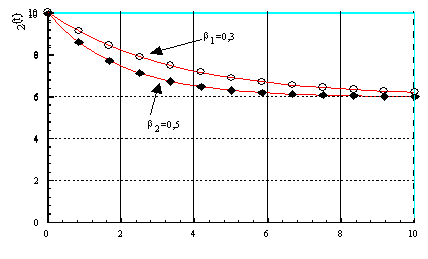
Рис.2 Графики функции E₂(t) для R₀ =6, E₀ = 10, b₁= 0,3 , b₂= 0,5.

Целесообразно обратить внимание на весьма любопытный момент, связанный с социальной психологией населения: величина b существенно зависит от уровня доверия населения к правительству страны и от направленности адаптации.

Чем меньше население доверяет государству, тем быстрее оно адаптируется к отрицательных тенденциям в динамике цен (имеет b₂ при E₀ < R₀ ) и тем медленнее оно реагирует на положительные тенденции (имеет b₁ при E₀ > R₀). Иначе говоря, население настроено на ухудшение экономической ситуации и относится с недоверием к наблюдаемым признакам улучшения (такой сценарий поведения типичен для российской экономики последнего десятилетия). Если же население настроено оптимистично к ожидаемым экономическим процессам, то ситуация обратная: оно быстро адаптируется к положительным тенденциям (имеет b₂ при E₀ > R₀) и медленнее реагирует на отрицательные тенденции (имеет b₁ при E₀ < R₀) в динамике цен.

Литература:

1. Справочник по математике для экономистов: Учеб. пособие/ Под ред. Проф. В.И. Ермакова. – 3-е изд., перераб. и доп. – М.: ИНФРА-М,2009. – 464с.

2. Высшая математика для экономических специальностей: Учебник и Практикум/ Под ред проф. Кремера Н.Ш. – М.: Высшее образования, 2009. – 893с.