Экономические науки/8.Математические методы в экономике.

Филиппова А.С., Бухарбаева Л.Я., Филиппов Д.В.

Уфимский государственный авиационный технический университет, Россия

Стохастические подходы решения задач транспортной логистики

С развитием рыночных отношений и ростом цен на продукты нефтяной промышленности проблема маршрутизации автотранспорта становится все более актуальной. При этом от решения этой проблемы напрямую зависит цена на товар, а в некоторых областях рынка затраты на доставку товара соизмеримы с его стоимостью. Одним из способов экономии ресурсов при транспортировке грузов является применение автоматизированных логистических систем, использующих для формирования рациональных маршрутов перевозки грузов эффективные экономико-математические методы. Предлагается подход к совершенствованию маршрутизации перевозок грузов путем создания общей алгоритмической платформы на базе стохастического подхода с использованием типовых моделей и математических методов решения задач транспортной логистики, которые составляют оптимизационное ядро логистической информационной системы.

Проблема формирования маршрутов для посещения заданного множества адресов некоторым количеством единиц транспортных средств (ТС) с обязательным возвращением в начальное местоположение после окончания поездки описывается классической задачей комбинаторной оптимизации – задачей коммивояжера [1]. Она является NP-трудной, следовательно, для ее решения не известно точного алгоритма решения полиномиальной сложности и с возрастанием размерности (количества городов). Поэтому разработка и применение на практике эффективных эвристических методов решения целесообразны.

Отметим, что для практического применения методов расчета маршрутов необходимо учитывать вместимость (грузоподъемность) транспортных средств. Постановка общей задачи следующая.

Задача маршрутизации с ограниченной вместимостью ТС, [2]. Предприятие со склада осуществляет доставку однородного товара клиентам. При полном удовлетворении потребностей клиентов необходимо минимизировать протяженность маршрутов и количество используемых транспортных средств ограниченной вместимости.

Представим задачу в математической интерпретации. Пусть – полный неориентированный граф; – множество вершин, где 0 – склад, 1,…,N – клиенты; – множество ребер; – расстояние между пунктами . Имеется парк одинаковых ТС вместимостью L; стоимость использования одного ТС составляет A; стоимость пробега 1 км составляет a. Для каждого клиента задан спрос .

Требуется составить множество маршрутов, удовлетворяющих следующим условиям: каждый маршрут начинается и заканчивается на складе; суммарный спрос для каждого маршрута не превосходит L; суммарные издержки минимальны 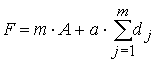, где m – число маршрутов (число использованных ТС), – суммарная длина маршрута j.

Решение поставленной задачи состоит из двух этапов:

1. решение задачи разбиения региона на компактные зоны обслуживания (группирование объектов-получателей для каждого маршрута). Это задача декомпозиции на региональные зоны;

2. решение задачи нахождения оптимального по заданному критерию (суммарному расстоянию, времени, стоимости доставки) порядка объезда получателей для каждого маршрута. Это задача маршрутизации.

После этих двух этапов формируются маршруты движения ТС с учетом их вместимости.

Для каждого этапа предлагается использовать стохастические методы решения. Для задачи кластеризации – построение остовного дерева по принципу разновероятностного чередования стратегии «в глубину» и «в ширину» [3]. Для задачи маршрутизации - модификация дихотомического варианта метода ветвей и границ. Рассмотрим подробнее эти этапы.

Для разбиения уменьшения размерности и разбиения на регионы общей транспортной сети, которая представлена в виде графа , строится случайное остовное дерево и выделяют на нем зоны (рис. 1.) При построении остовного дерева экспериментально установлен эффективный диапазон для частоты применения стратегий «в ширину» и «в глубину» присоединения очередной вершины, который равен p2=[0,8;1] и p1=[0;0,2] соответственно.

2516582400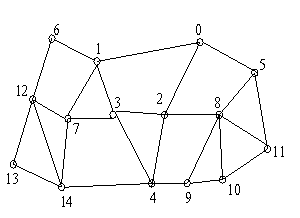2516572160

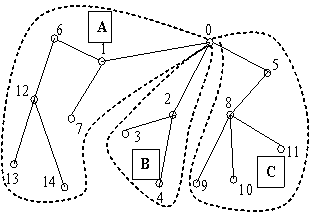
a b

Рис. 1. Транспортная сеть: а – граф; b – остовное дерево и зоны обслуживания A, B, C

На втором этапе для каждой зоны строят маршруты. Для этого применяется модифицированный алгоритм на базе дихотомического метода ветвей и границ со случайным выбором вершины ветвления. Для метода ветвей и границ основными являются две процедуры: ветвление и нахождение оценок (границ). Процедура нахождения оценок заключается в поиске верхних и нижних границ для оптимального значения на подобласти допустимых решений. Если нижняя граница для подобласти B’ дерева поиска больше, чем верхняя граница какой-либо ранее просмотренной подобласти B, то B’ может быть исключена из дальнейшего рассмотрения (правило отсева). Классический вариант дихотомии – это усечение полного просмотра областей допустимых решений (ветвей), потенциально содержащих оптимальное решение, и разбиением только на две подобласти, из которых выбирают с меньшей оценкой. Дихотомия означает деление пополам, т.е. в ходе решения задачи маршрутизации получаем некое разбиение на путь, содержащий одно из ребер графа и не содержащий его, [1]. Но при подобном усеченном просмотре возможных решений, оптимальное решение может быть не достигнуто.

Стохастический модифицированный вариант дихотомии основан на следующем. При подсчете оценок могут быть получены несколько минимальных значений для потенциальных вершин ветвления дерева решений, дихотомический способ должен выбрать только одну из них. В этом случае используется вероятностный способ определения такой вершины. Этот подход применяется для нахождения рационального маршрута в каждой зоне.

Для исследования эффективности разработанных стохастических методов решения общей задачи маршрутизации проведен вычислительный эксперимент. Координаты городов генерировались как независимые случайные числа, размерность задач N=10, 25, 50, 100 городов, ТС с грузоподъёмностью L =1500 ед. В ходе проведения эксперимента были выделены следующие классы задач: класс A – нет разбиения на регионы (1 регион); класс B – количество регионов задано небольшое и небольшие весовые потребности у клиентов; класс C –количество регионов задано небольшое и большие весовые потребности у клиентов; класс D – количество регионов задано большое и небольшие весовые потребности у клиентов; класс E – количество регионов задано большое и большие весовые потребности у клиентов.

Вычислительный эксперимент позволил сделать следующие выводы. Стохастический способ разбиения на зоны с использованием чередования стратегии «в глубину» и «в ширину» сокращается количество транспортных средств от 1% до 3%. Для исходных данных классов А и В, лучшие результаты показывает классический метод дихотомии с использованием стохастического способа разбиения на зоны, сокращая общую протяженность маршрутов в среднем на 5-10%. В случаях, когда количество регионов большое (класс D и E), стохастический вариант дихотомии показывает лучшие результаты, чем классический, и сокращает общую протяженность маршрутов на 1-3%.

Используя стохастические методы зонирования и формирования маршрутов движения ТС, уменьшая общую протяженность маршрутов доставки товара, можно уменьшить затраты на рейсы, а значит и увеличить доход фирмы. Эффект использования математических методов формирования рациональных маршрутов наиболее проявляется при масштабных грузоперевозках, в особенности, когда время доставки не позволяет использовать возможность накопления грузов в течение длительного времени и доставки более крупногабаритным транспортом.

Литература:

1. Филиппова А.С., Филиппов Д.В. Гильманова Н.А. Задачи маршрутизации в транспортных логистических системах: локальный поиск оптимальных решений // Информационные технологии. №2, 2009. с.59-63.

2. Сигал И.Х., Иванова А. П. Введение в прикладное дискретное программирование: модели и вычислительные алгоритмы: Учеб. Пособие/— Изд. 2-е, испр. и доп. — М. : ФИЗМАТЛИТ, 2007 .— 304 с.

3. Ху Т.Ч., Шинг М.Т. Комбинаторные алгоритмы. Перевод с англ. В.Е. Алексеева, Н.Ю.Золотых и др. – Нижний Новгород. Изд-во Нижегородского госуниверситета им. Н.И.Лобочевского, 2004. –329 с.