География и геология/7.
Техника и технология геологоразведовательных работ
Кочнев А.П, Мисюркеева Н.В
Научно Исследовательский Иркутский Государственный Технический
Университет, Россия
ЭЛЛИПСОИД
КАК ФИГУРА АППРОКСИМАЦИИ ФОРМЫ ЖИЛЬНЫХ СЛЮДОНОСНЫХ ПЕГМАТИТОВЫХ ТЕЛ
Проблема аппроксимации формы жильных рудных тел геометрическими
фигурами детально не разработана как в целом для месторождений любых полезных
ископаемых, так и для месторождений слюдоносных пегматитов, хотя в процессе
разведки, оконтуривания и подсчета запасов приходится неизбежно решать задачу
геометризации изучаемых объектов. На практике она решается обычно интуитивно
без серьезных обоснований.
Так, по данным В.М. Крейтера [1] при разведке рудных
тел наземными горными выработками с применением буровых скважин оконтуривание
их на глубину проводится формально – внешний контур проводится в зависимости от
размеров рудного тела с учетом плотности сети разведочных выработок. Обычно
применяется способ неограниченной экстраполяции в тех случаях, когда нет
сколько-нибудь убедительных геологических данных о границах распространения
оруденения за пределы участка, освещенного разведочными выработками.
При этом внешний контур проводится:
1) параллельно внутреннему на расстоянии, равном
расстоянию между разведочными выработками или половине среднего расстояния
между ними (для морфологически неустойчивых тел полезного ископаемого);
2) в зависимости от длины тела полезного ископаемого,
образуя треугольник, у которого высота принимается равной половине длины тела
полезного ископаемого (рис. 1, а), или прямоугольник с высотой, равной четверти
длины тела полезного ископаемого (рис. 1, б);
3) по поверхности конуса (для изометрических тел), основанием
которого служит площадь сечения тела полезного ископаемого, ограниченная внутренним
контуром, а высота равна половине среднего поперечного размера тела (рис. 1,
в). Иногда на этом же основании строится полушарие.
Все эти приемы оконтуривания месторождений являются в
значительной мере субъективными и ничем не обоснованными. Поэтому их
рекомендуется по возможности избегать.
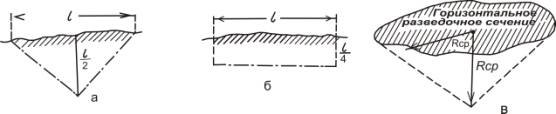
Рис. 1.
Проведение внешнего контура в зависимости от длины тела по простиранию (по
В.М.Крейтеру, 1961):
а – по правилу
треугольника; б – по прямоугольному полотну; в – по поверхности конуса
При
детализации разведки неограниченная экстраполяция сменяется по всей периферии
тела полезного ископаемого экстраполяцией ограниченной и, таким образом, залежь
оконтуривается достаточно точно. Однако всегда желательно представлять общие
контуры месторождения как можно раньше – и для решения перспективных вопросов
эксплуатации месторождения и для рационального направления дальнейших детальных
разведочных работ. Поэтому в практике разведки контуры тела полезного
ископаемого в первом приближении устанавливаются редкой сетью разведочных
выработок.
Принимаемые
в упомянутых случаях ограничения глубины подвески подсчетного блока ½
или ¼ часть длины рудного тела на поверхности отражают эмпирическую
закономерность о равной вероятности любого уровня эрозионного среза рудного
тела, которая в среднем статистически равна 50%.
Аналогично поступают и на начальных стадиях разведки слюдоносных
пегматитовых жил наземными горными выработками. Форма слюдоносных жил по
аналогии с рудными телами традиционно отождествляется с пирамидой или призмой
(правило Гувера), а в более сложных случаях – с усеченной пирамидой, имеющей в
продольном сечении форму трапеции [2,3].
Анализ материалов по
разведке жил Мамских, Карельских и Бирюсинских месторождений слюды [2]
показывает, что такой подход не обеспечивает необходимой точности оценки
запасов – по большинству вовлеченных в эксплуатацию жил зафиксирована неоправданность
подсчитанных при разведке запасов.
По нашему мнению одной из
основных причин такого положения является неудачный недостаточно обоснованный
выбор геометрических фигур, аппроксимирующих форму слюдоносных жил. Пирамида и
призма не позволяют отобразить все особенности поведения жил в пространстве,
однозначно трактуют соотношения длины и глубины жил, не учитывают погружение и
склонение жильных тел и т.д.
Представляется, что этим
условиям больше отвечает трехосный эллипсоид, которым можно считать наиболее
оптимальной фигурой аппроксимации формы слюдоносных пегматитовых жил.
Предпочтительность
эллипсоида для решения задач разведки, оконтуривания и подсчета запасов
слюдоносных жил обосновывается следующими обстоятельствами:
-
эллипсоид имеет четкие
геометрические границы;
-
не имеет показателя уходящего
в бесконечность (в отличие от таких фигур как призма, пирамида, цилиндр) и,
следовательно, не требует дополнительных ограничений области действия;
-
имеет три оси симметрии
и может принимать различные формы от шара до плоско вытянутых фигур с
естественным выклиниванием, отражающих частные формы слюдоносных пегматитовых
жил (таблица).
-
параметры уплощенного
трехосного эллипсоида четко коррелируются с параметрами жил – протяженность его
по длинной оси (2а) отвечает истинной длине жил, размер по короткой оси (2с)
соответствует мощности жил, а размер по средней оси (2в) отождествляется с глубиной;
Основные формы рудных тел, аппроксимированных
трехосным эллипсоидом
|
№ |
Основные формы |
Соотношение параметров |
Формы тел |
|
Ф1 |
|
а:в:с=1:1:1 (а=в=с) |
шарообразные (изометричные) тела, гнезда, штоки, штокверки |
|
а:в:с=2:2:1 (в=а, с=0.5а) |
|||
|
Ф2 |
|
а:в:с=2:1:1 (в=0.5а, с=0.5а) |
брусковидныее (столбообразные) тела с овальным сечением |
|
а:в:с=4:4:1 (в=а, с=0.25а) |
|||
|
Ф3 |
|
а:в:с=4:2:1 (в=0.5а, с=0.25а) |
уплощенно-брусковидные тела с овальным сечением |
|
а:в:с=4:1:1 (в=0.25а, с=0.25а) |
|||
|
Ф4 |
|
а:в:с=10:10:1 (в=а, с=0.1а) |
линзовидные тела с линзовидным сечением, |
|
а:в:с=10:4:1 (в=0.4а, с=0.1а) |
|||
|
а:в:с=10:2:1 (в=0.2а, с=0.1а) |
|||
|
а:в:с=10:1:1 (в=0.1а, с=0.1а) |
|||
|
|
|
а:в:с=20:20:1 (в=а, с=0.05а) |
уплощенно-линзо-видные тела с пластинчатым сечением,
пластообразные (плитообразные) |
|
а:в:с=20:10:1(в=0.5а, с=0.05а) |
|||
|
а:в:с=20:4:1 (в=0.2а, с=0.05а) |
|||
|
а:в:с=20:2:1 (в=0.1а, с=0.05а) |
|||
|
а:в:с=20:1:1(в=0.05а, с=0.05а) |
-
пространственная
ориентировка длинной оси отражает направление погружения и склонения жил,
ориентировка плоскости а-в – падение жилы;
-
сложные по морфологии
жилы могут быть отображены комбинацией нескольких разномасштабных эллипсоидов;
-
закономерные соотношения
параметров эллипсоида позволяют упростить процедуру оконтуривания и подсчета
запасов с применением известного математического аппарата.
Анализ параметров детально разведанных и отработанных
слюдоносных жил Мамской мусковитоносной провинции показывает, что при
оконтуривании жил и подсчете запасов используются видимые, оцененные в
случайном эрозионном срезе, а не истинные параметры жил. Так, длиной считается
протяженность жил по простиранию, мощностью – ширина выхода жилы вкрест простирания,
а глубиной – протяженность жил по падению. Истинные же параметры могут быть
оценены, когда достоверно установлено склонение жилы: длиной ее, как мы уже
отмечали, является протяженность по склонению, т.е. по оси «а» уплощенного
трехосного эллипсоида, глубиной – протяженность ее в поперечном сечении
относительно направления склонения, т.е. по оси «в» эллипсоида, а мощностью –
размер по короткой оси «с» эллипсоида.
Следовательно, размеры рудных тел должны
характеризоваться не тремя (длина, мощность, глубина), а целым комплексов
параметров:
-истинная
длина – протяженность тела по линии погружения (склонения), т.е. по оси «а» эллипсоида,
-видимая
длина по простиранию – протяженность тела по линии простирания,
-видимая
длина по линии эрозионного среза,
-истинная
глубина – разность гипсометрических отметок эрозионной поверхности и точки выклинивания
по линии склонения,
-видимая
глубина по падению – протяженность тела по линии падения,
-видимая
глубина по склонению – протяженность тела по линии склонения (погружения).
В соответствии с этим
пространственное положение рудного тела должно определяться как традиционными
элементами залегания (азимут простирания, азимут падения, угол падения), так и
дополнительными элементами залегания – азимутами и углами погружения,
склонения, восстания и воздымания. Все эти элементы залегания эллипсоидального
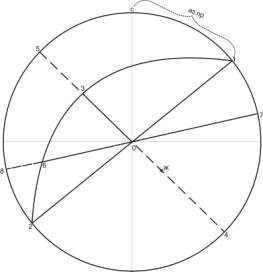
рудного тела могут быть четко опреде- лены с помощью сферограммы (рис. 2).
|
|
На
рис. 2 отрезок 1-2 соответствует проекции линии простирания, отрезок 0-3 –
проекции линии падения, угол С-О-1 – азимут простирания, угол С-О-4 – азимут
падения, 3-5 – угол падения, 0-6 – проекция линии склонения (погружения),
угол С-О-7 – азимут склонения (погружения), 6-8 – угол погружения, угол 6-О-2
– угол склонения, угол С-О-5 – азимут восстания, дуга 1-3-6-2 –
граммапроекция осевой плоскости жилы, точка Ж – гномопроекция осевой
плоскости жилы. |
|
Рис. 2. Сферограмма
элементов залегания пегматитовой жилы |
Литература:
1. Крейтер В.М. Поиски и разведка месторождений
полезных ископаемых. Ч.2. – М.: Госгеолтехиздат, 1961. – 390 с.
2. Родионов Г.Г., Роненсон Б.М. Оценка месторождений
при поисках и разведках: Слюда. – М.: Недра, 1972. – 216 с.
3. Францкий И.В. Математическая статистика и геометризация месторождений.
– Иркутск, 1975. – 249с.