УДК 517.43
О возможной скорости роста нормированных собственных
функций задачи типа Редже на непрерывных весовых функциях и весовых функциях
близких к функциям из классов Гельдера
Айгунов Г.А., Жвамер Карван Х.
Пусть ![]() - фиксированные
числа. Обозначим через
- фиксированные
числа. Обозначим через ![]() совокупность всех
суммируемых на
совокупность всех
суммируемых на ![]() функций
функций ![]() , удовлетворяющих условию
, удовлетворяющих условию ![]() . В дальнейшем такие функции будем называть весовыми
функциями.
. В дальнейшем такие функции будем называть весовыми
функциями.
Рассмотрим спектральную задачу (![]() )
)
![]() (
(![]() ) (1)
) (1)
![]() ,
, ![]() (2)
(2)
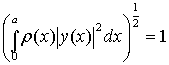 , где
, где ![]() . (3)
. (3)
Эта задача рассматривалась в работах
[1]-[3], где доказано, что для гладких весовых функций ![]() собственные функции задачи (1)-(3) равномерно ограничены,
если
собственные функции задачи (1)-(3) равномерно ограничены,
если ![]() и растут как
и растут как ![]() в случае
в случае ![]() . Для суммируемых весов в этих работах установлено, что
собственные функции могут расти как
. Для суммируемых весов в этих работах установлено, что
собственные функции могут расти как ![]() на некоторой
подпоследовательности собственных функций
на некоторой
подпоследовательности собственных функций ![]() . Заметим, что для задачи типа Штурма-Лиувилля в случае
гладких весов собственные функции равномерно ограничены.
. Заметим, что для задачи типа Штурма-Лиувилля в случае
гладких весов собственные функции равномерно ограничены.
Данная работа посвящена изучению поведения
собственных функций задачи (1)-(3) для весовых функций из промежуточных
классов.
Аналогичное изучение поведения собственных
функций для задачи Штурма-Лиувилля рассмотрено в работах [4]-[5].
В классе непрерывных весовых функций
справедлива следующая
Теорема
1. Для любой последовательности ![]() существует
непрерывная весовая функция
существует
непрерывная весовая функция ![]() такая, что
такая, что
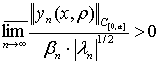 .
.
Рассмотрим класс весовых функций ![]() , удовлетворяющих условиям Гельдера
, удовлетворяющих условиям Гельдера ![]() , где
, где ![]() ,
, ![]() . Обозначим этот класс через
. Обозначим этот класс через ![]() . Справедлива следующая
. Справедлива следующая
Теорема
2. Пусть ![]() ,
, ![]() и
и ![]() . Тогда существует весовая функция
. Тогда существует весовая функция ![]() удовлетворяющая
условиям:
удовлетворяющая
условиям:
1)
![]() ;
;
2)
![]() имеет счетное
множество
имеет счетное
множество ![]() точек разрыва первого
рода таких, что
точек разрыва первого
рода таких, что ![]() и для любого
и для любого ![]() на
на ![]() конечное число точек из
конечное число точек из
![]() ;
;
3)
на участках ![]() ,
, ![]() ,…,
,…, ![]() ,… функция
,… функция ![]() удовлетворяет условию
Гельдера с теми же
удовлетворяет условию
Гельдера с теми же ![]() и
и ![]() , что и
, что и ![]() ;
;
4)
скачки ![]() удовлетворяют
неравенствам
удовлетворяют
неравенствам
![]() ;
;
5)
Если ![]() - собственные числа и
функции задачи (1)-(3) с весом
- собственные числа и
функции задачи (1)-(3) с весом ![]() , то
, то
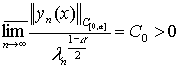 .
.
Таким образом, на весовых функциях из
промежуточного класса между гладкими и суммируемыми весовыми функциями также
возможен рост нормированных собственных функций задачи (1)-(3), как ![]() , где
, где ![]() .
.
Доказательства теорем 1 и 2 опирается на
теорему о непрерывной зависимости собственных значений от весовых функций [3],
лемму из [2] и следующее следствие этой леммы.
Следствие. Пусть ![]() и
и ![]() произвольные
фиксированные числа, а
произвольные
фиксированные числа, а ![]() - множество весовых
функций
- множество весовых
функций ![]() , удовлетворяющих соотношению
, удовлетворяющих соотношению ![]() . Тогда существует константа
. Тогда существует константа ![]() , зависящая только от
, зависящая только от ![]() и номер
и номер ![]() такие, что для
такие, что для ![]() непрерывная весовая
функция
непрерывная весовая
функция ![]() такая, что, если
такая, что, если ![]() , то
, то ![]() ,
, ![]() и справедливо
неравенство
и справедливо
неравенство
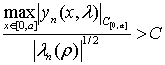 .
.
Литература
[1] Айгунов Г.А., Гаджиева Т.Ю. Сб. «Функц.-диф.
ур-я и их приложения», г. Махачкала, 2009 г. С.18-26.
[2] Айгунов Г.А., Жвамер Карван Х. УМН,
2009 г., т. 64, №6.C. 169-170.
[3] Айгунов Г.А., Жвамер Карван Х. Изв. вузов,
Сев. Кав. регион. Ростов на Дону,
ест. науки, 2010 г., №2. С.8-12.
[4]
Айгунов Г.А., Гехтман М.М. УМН, 1997 г., т. 52, №3, с. 161-162.
[5] Айгунов Г.А. УМН, 1997 г., т. 52, №6,
с. 147-148.