Виконавець: Чорний А. В.

Буковинська державна фінансова академія

Дослідження надмірності інформації в економіці

У даній роботі об'єктом дослідження є сукупність спостережуваних економічних даних у вигляді дискретних і неперервних розподілів стохастичних величин.

Предметом дослідження є розгляд теоретичних і практичних проблем кількості інформації (ентропії) та надмірності інформації економічних даних у числовій формі.

Метою роботи є визначення надмірності кількості інформації та встановлення її зв’язку з ентропією та числовими характеристиками розподілів економічних стохастичних величин.

При економічному дослідженні дискретна або неперервна стохастична величина задана певним розподілом всередині деякого із відрізків довжиною на числовій осі набуває значення . Ймовірність знаходження значення випадкової величини в кожному відрізку може бути різною і дорівнювати . Кількість інформації, яку можна отримати від дослідження одного інтервалу при пошуках місця розташування в межах ряду розподілу, характеризується математичним сподіванням логарифма ймовірності:

(1)

Повна кількість інформації яку можна отримати при дослідженні того в якому інтервалі знаходиться визначиться наступним чином:

(2)

У теорії інформації кількісна міра інформації називається ентропією і позначається Ентропія неперервних процесів і явищ розглядається як граничний випадок ентропії дискретного розподілу. Ймовірність того, що прийме те чи інше значення, характеризується функцією щільності ймовірності . Кількісну оцінку ентропії неперервного процесу отримаємо граничним переходом від суми до інтеграла:

(3)

де - найменший інтервал змінної , з точністю до якої вона може бути визначена.

Визначимо для найбільш поширених розподілів яку кількість інформації можна отримати на всьому інтервалі можливих значень випадкової величини та проведемо аналіз інформаційної надмірності. Спочатку використаємо метод дискретизації інтервалу по координаті згідно з теоремою відліків. Якщо функція визначена на кінцевому інтервалі і має спектр Фур’є, обмежений максимальною частотою , то загальна кількість відліків функції на інтервалі буде дорівнювати:

, (4)

де є кількість інтервалів дискретизації. Функція визначається кінцевим рядом:

, (5)

де - функція відліків.

Якщо є кількість відліків, то для кількості інформації, згідно (2) отримуємо:

. (6)

Якщо щільність ймовірності однакова у всіх точках відліку (випадковий стаціонарний процес), то при відсутності статистичного зв’язку між відліками в будь-яких двох точках ентропія всієї сукупності точок відліку буде дорівнювати:

. (7)

Якщо між окремими відліками випадкової функції існує кореляційний зв’язок, то для знаходження загальної кількості інформації необхідно спочатку знайти сумісну функцію щільності ймовірності всієї сукупності точок і скористатися - кратним інтегралом:

(8)

Визначимо ентропію найбільш поширеного нормального розподілу:

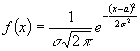(9)

Спочатку знайдемо математичне сподівання та дисперсію. Математичне сподівання неперервної випадкової величини дорівнює 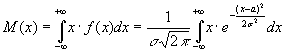. Введемо нову змінну . Звідси , .

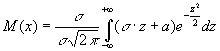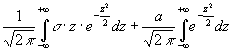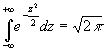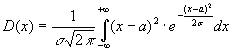Отже =. В першому доданку під знаком інтеграла непарна функція, межі інтегрування симетричні відносно початку координат і тому перший інтеграл дорівнює нулю. В другому доданку інтеграл Пуассона . Тому другий доданок дорівнює та математичне сподівання . Дисперсія неперервної випадкової величини, враховуючи, що дорівнює . Введемо нову змінну . Звідси , . Отже 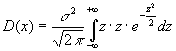. Проінтегруємо по частинах, поклавши і знайдемо, що дисперсія і середнє квадратичне відхилення (стандарт) дорівнює =.

Тепер визначимо ентропію нормального розподілу, використовуючи формулу (3):

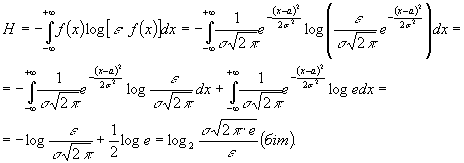(10)

При виведенні цієї формули було враховано:

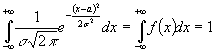та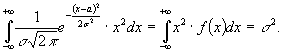

Тепер знайдемо ентропію рівномірного розподілу. Неперервний

рівномірний розподіл випадкової величини на відрізку [a,в], де а,в , має щільність ймовірності

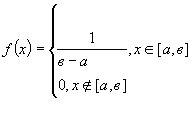. (11)

Функція розподілу ймовірностей:

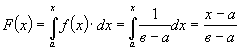. (12)

Ентропія рівномірного розподілу:

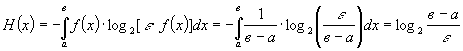. (13)

Якщо відома ентропія, то можна визначити інформаційну надмірність спостережуваних економічних стохастичних даних. Для виміру надмірності інформації використаємо вже вказану формулу [2]:

, (14)

де - максимально можлива кількість інформації, - реальна кількість інформації.

Використовуючи таке означення надмірності можна записати:

. (15)

Надмірність, обумовлена нерівноймовірним розподілом буде дорівнювати:

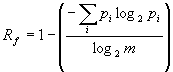. (16)

Надмірність, викликана статистичним зв'язком між значеннями :

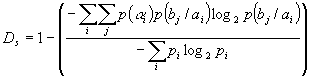. (17)

Повна інформаційна надмірність:

. (18)

Для нормального та рівномірного законів розподілу, використовуючи таке означення надмірності, можна значення визначати по формулам (10) і (13), а значення буде визначатись згідно (6), реально отриманою у досліді кількістю відліків .

Економічне явище вибірково себе поводить до сполучень відліків і до різних їх комбінацій. Тобто хід явища завжди йде таким чином, що певною мірою зберігається закон розподілу відліків - стохастичних величин. У разі, якщо відліки мають певний кореляційний зв'язок, то його потрібно враховувати, оскільки кореляція відліків зменшує кількість ентропії на один відлік. Тоді буде визначатися через число відліків по теоремі відліків, згідно (4).

Слід відмітити, що на практиці значення може бути визначене по формулі (3) і через , яке залежить від конкретних умов вимірювання та від точності вимірювальної апаратури.

Немає сенсу робити менше похибки вимірювань, тому що інформація всередині такого інтервалу буде недостовірною.

Щодо , то для його визначення , при найпростішому кореляційному зв’язку, використаємо такий вираз:

, (19)

де - відносна частота появи - го відліку, - відносна частота появи -го

відліку безпосередньо після -го в заданій вибірці.

Використовуючи в (15) всі точки по теоремі відліків, отримуємо надмірність . Якщо ж , то надмірність близька до свого максимального значення . Надмірність потрібна тому, що якби її не було, то довелося би уловлювати кожну точку (відлік), інакше не можливо було би відтворити хід певного економічного явища. Нехай при дослідженні економічного явища отримано відліків, які становлять від всіх , визначених теоремою відліків. Ці відліків не корелюють між собою і є неочікуваними, тобто вони несуть більше інформації в порівнянні з тим, якщо б вони стояли поруч на сусідніх інтервалах, коли потрібно враховувати кореляцію. Відліки несуть кількість інформації рівну , де можна визначати, в залежності від задачі, наприклад, по (10) або (13).

Але для відліків по теоремі відліків інформаційна ціна з урахуванням кореляційних зв’язків буде , наприклад, по (19). Тоді кількість інформації, що неодмінно відтворить хід економічного явища дорівнює . Звідси отримуємо наступну умову:

, або , яка вказує на те, що для принципового відтворення закону розподілу стохастичних величин економічного явища, необхідно, щоб надмірність у відсотках була не меншою відсотка втрачених відліків.

Таким чином, в даній роботі визначено кількість інформації для нормального та рівномірного розподілів, надмірність інформації для дискретних і неперервних розподілів економічних стохастичних величин заданих в числовій формі з використанням теореми відліків, урахуванням властивостей розподілів економічних величин та їх залежності від умов вимірювання і точності вимірювальної апаратури.

Список використаних джерел

1. Шарапов О. Д. Економічна кібернетика: навч. посібник / О. Д. Шарапов, В. Д. Дербенцев, Д. Є. Семьонов. — К.: КНЕУ, 2004. — 231 с.

2. Осовська Г.В. Основи менеджменту. навчальний посібник / Г.В. Осовська, О.А. Осовський. — К.: "Кондор", 2006. — 664 c. Режим доступу: http://www.info-library.com.ua/books-text-5538.html.

3. Аналіз процесу передачі інформації. [Електронний ресурс] — Режим доступу: http://referat-kursova.ru/referat-kursova/analiz-procesu-peredachi-informaciyi-1867.html.

4. Показники оцінки вірогідності (безпомилковості) передачі даних у мережах. [Електронний ресурс] — Режим доступу: http://autonews.cc.ua/ pokazniki-ocnki-vrogdnost-bezpomilkovost-peredach-danih-u-merezhah.html.

5. Різник В. Проблема подолання інформаційної надмірності монолітного коду / В. Різник, В. Парубчак, Д. Скрибайло-Леськів. [Електронний ресурс] — Режим доступу: http://www.nbuv.gov.ua/portal/natural/Vnulp/Komp-nauky/2008_629/05.pdf.