Математика/4.
Прикладная математика
К.т.н. Хливненко Л.В.,
к.ф.-м.н. Васильев В.В., д.м.н. Пятакович Ф.А.
Воронежский государственный
технический университет,
Воронежский государственный университет,
Белгородский государственный национальный исследовательский университет, Россия
Нейросетевое
решение задачи классификации степени
активности
автономной нервной системы
В настоящее
время интенсивно развивается направление реабилитационной медицины, связанное с
использованием биологической обратной связи [1]. При реализации такого рода
систем необходима непрерывная обработка большого потока электрофизиологической
информации. Высокая производительность интеллектуальных систем обработки электрофизиологической
информации может быть достигнута за счет выполнения интеллектуальных ядер в
виде нейросетевых модулей [2,3,4]. Обученные нейросетевые системы оказываются
более выигрышными в плане временных затрат на обработку эмпирических данных,
обеспечивая при этом такие полезные свойства систем, как нелинейность, адаптивность,
отказо- и помехоустойчивость
В данной работе
рассматривается обучение, функционирование и оценка эффективности двухслойной
прямонаправленной искусственной нейронной сети, построенной для решения задачи
автоматического распознавания степени активности автономной нервной системы
(АНС) у здоровых лиц, находящихся в различных функциональных состояниях.
Использованы методы математического анализа, математической статистики,
системного анализа, математического и компьютерного моделирования. Компьютерная
реализация искусственной нейронной сети выполнена в свободно распространяемой
среде программирования Lazarus.
Рассматривается
вектор межпульсовых интервалов, получаемый с помощью блока ввода
электрофизиологической информации, включающего датчик пульса. Исходный временной
ряд разбивается на участки, каждый из которых содержит два уровня измерения
сигнала. Последующий участок сдвигается по отношению к предыдущему на один
временной такт. Пара, составленная из предыдущего и последующего межпульсовых
интервалов, «скользит» по временному ряду с шагом, равным единице. Каждая пара
определяет временную составляющую из нулевых, укорачивающих и удлиняющих
коррекций межпульсовых интервалов.
Вводится в
рассмотрение непрерывная случайная величина X, значения которой связываются
с длиной и видом коррекции. Все наблюдаемые значения признака X
попадают в интервал 
, который проходится с шагом 
.
Таким образом,
алфавит системы включает 61 класс дифференциальной гистограммы распределения паттерна
вариабельности ритма сердца, включающий норму, тахи- и брадиаритмию. Вычисления
проводили по 500 коррекциям.
Информационные
показатели модели соответствуют параметрам энтропии ритма сердца. Так
нормированная энтропия 
характеризует меру
хаоса ритма сердца и отражает степень активности АНС [5].
В
экспериментальной части работы были проанализированы 189 записей межпульсовых
интервалов у 94 практически здоровых студентов Белгородского государственного
университета. Все обследуемые входили в одну социальную и возрастную группу от
17 до 24 лет [6].
В результате
были получены шесть интервальных классов нормированной энтропии, которые
соответствовали известным функциональным состояниям и дифференцированной
степени активности АНС человека:
- РВП СНС (Резко выраженное
преобладание симпатической нервной системы);
- ВП СНС (Выраженное
преобладание симпатической нервной системы);
- УП СНС (Умеренное
преобладание симпатической нервной системы);
- НОРМА (Равновесное состояние
между симпатикусом и парасимпатикусом);
- УП ПСНС (Умеренное
преобладание парасимпатической нервной системы);
- ВП ПСНС (Выраженное
преобладание парасимпатической нервной системы).
В нашем
исследовании вычисленная нормированная энтропия использовалась для формирования
мнения эксперта и целевых выходных векторов 
, предназначенных для обучения искусственной нейронной сети.
Позиция правильного выходного класса маркировалась в целевом векторе значением
0,5. Остальные координаты целевого вектора принимали значение: - 0,5.
На входы
искусственной нейронной сети подавались частоты интервального вариационного
ряда, соответствующие реализациям случайной величины Х в алфавите системы.
Входы сети 
, 
, были подвергнуты процедуре нормализации за счет вычитания
их выборочного среднего и нормирования на квадратный корень из их исправленной
выборочной дисперсии.
Активность
нейронов скрытого слоя 
, 
, вычислялась по формулам: 
, где 
- весовой коэффициент связи между 
-м
входом и 
-м
нейроном скрытого слоя. В качестве активационной функции был взят
гиперболический тангенс, называющийся в теории нейросетевого моделирования
также биполярным сигмоидом: 
Активность
нейронов выходного слоя 
, 
, вычислялась по формулам: 
, где 
- весовой коэффициент связи между 
-м
нейроном скрытого слоя и 
-м
нейроном выходного слоя, 
Номер нейрона
выходного слоя, имеющего максимальную активность, служит маркером класса, к
которому сеть относит входной пример.
При обучении
искусственной нейронной сети ставилась задача минимизации целевой функции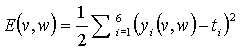 
.
При
инициализации сети все весовые коэффициенты принимали случайные значения из
отрезка 
.
В процессе
обучения пошаговая корректировка весов выполнялась в направлении антиградиента
целевой функции по формулам:
, 
,
(1)
где 
- дискретный момент
времени, 
- скорость обучения.
В нашем исследовании 
.
Оценим по
выборке 
, где 
- объем выборки,
величины 
и 
.
, 
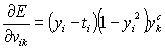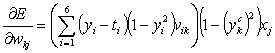. (2)
Введем
обозначение 
, тогда формулы (2) примут вид
,
.
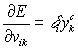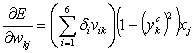(3)
С учетом (3)
ключевые формулы метода модификации весовых коэффициентов связи (1) будут иметь
следующий вид:
, 
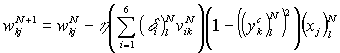. (4)
Корректировка
синаптических коэффициентов связи продолжалась до тех пор, пока не достигался
приемлемый уровень ошибок I и II-го рода на обучающей и контрольной
выборках.
В среднем после
30000 обучающих эпох (время обучения – 2 мин) сеть устойчиво выходит на 90%
верной классификации и ошибается только в граничных случаях.
В табл.1
приведены результаты эффективности прогнозирования степени активности АНС,
полученные по обучающему множеству примеров.
Таблица
1.
|
|
|
Правильно |
Неправильно |
||
|
Ист+ |
Ист- |
Гиподиаг-ностика |
Гипердиагностика |
||
|
Итого: человек, % |
139-100% |
97-70% |
36-26% |
0 - 0% |
6 – 4% |
На обучающей
выборке двухслойная искусственная нейронная сеть правильно классифицировала 96%
примеров. Неправильно распознано – 4%.
Чувствительность системы составила 100%, специфичность дифференциальной
диагностики – 86,7%.
В табл.2
приведены результаты эффективности прогнозирования степени активности АНС,
полученные по контрольному множеству примеров.
Таблица
2.
|
|
|
Правильно |
Неправильно |
||
|
Ист+ |
Ист- |
Гиподиаг-ностика |
Гипердиагностика |
||
|
Итого: человек, % |
50-100% |
34-68% |
12-25% |
1 - 2% |
3 – 5% |
На контрольной
выборке двухслойная искусственная нейронная сеть правильно классифицировала 93%
примеров. Неправильно распознано – 7%, что существенно ниже ошибок
распознавания, допускаемых врачом. Из них гипердиагностика составила 5%, гиподиагностика
2%. Чувствительность системы составила 97,1%, специфичность дифференциальной
диагностики – 83,3%.
Литература:
1. Pyatakovich F.A. Biotechnical system of car game training based on
use of a multiparametrical feedback and subsensitivity light signals of
control/ F.A. Pyatakovich, T.I. Yakunchenko// European journal of natural
history, № 6, 2009. - p. 38-40.
2. Хливненко Л.В. Возможности решения медицинских
диагностических задач с помощью проектирования обучающихся искусственных
нейронных сетей/ Л.В. Хливненко, В.В. Васильев, Ф.А. Пятакович // Успехи
современного естествознания: научный журнал,
№ 12, 2010. - с. 75-79.
3. Хливненко Л.В. Прогнозирование исходов мерцательной
аритмии с помощью искусственной нейронной сети/ Л.В. Хливненко // Информатика:
проблемы, методология, технологии: материалы 7-й межд. науч.-метод. конф., 8-9
февраля 2007 г. - Воронеж, 2007. - с. 467-471.
4. Пятакович Ф.А. Алгоритмы классификации степени
активности автономной нервной системы на базе нейрокомпьютинга/ Ф.А. Пятакович,
Л.В. Хливненко, Т.И. Якунченко// Международный журнал фундаментальных и
прикладных исследований, № 5, 2010. - с. 115-119.
5. Пятакович Ф.А. Модели и алгоритмы нейросетевой
дифференциации классов функционального состояния вегетативной нервной системы/
Ф.А. Пятакович , Л.В. Хливненко, В.В. Васильев, О.В. Маслова// Системный анализ
и управление в био-медицинских системах: журнал практической и теоретической биологии
и медицины, Т.9, № 4, 2010. – с. 870-874.
6. Пятакович Ф.А. Разработка моделей и алгоритмов
нейросетевой классификации степени активности автономной нервной системы и
оценка их адекватности на обучающей и экзаменационной выборках / Ф.А. Пятакович
, Т.И. Якунченко, Л.В. Хливненко, В.В. Васильев, К.Ф. Макконен, О.В. Маслова//
Фундаментальные исследования, № 2, 2011. – с. 136-141.