Математика/4. Прикладная математика
Баумгертнер
С.В., Мельников Б.Ф.
Тольяттинский
государственный университет, Россия
Anytime-алгоритм поиска псевдо-оптимального регулярного выражения для заданного конечного автомата
Рассматривается задача построения регулярного выражения с
минимальной звёздной высотой для заданного недетерминированного
конечного автомата. Предлагается anytime-алгоритм[2], позволяющий
получать как точные, так и приближённые решения данной задачи.
Определим по индукции звёздную
высоту регулярного выражения r (обозначим ее sh(r)) :
1.
sh(Ø)=sh(Ø*)=sh(a)=0 для всех a Є ∑.
2. Пусть r и s – произвольные регулярные выражения. Тогда
sh((r+s))=sh((r·s))=max(sh(r),sh(s)).
3.
Для любого регулярного
выражения r sh((r*))=sh(r)+1.
Звёздная высота регулярного языка есть минимальная из звёздных высот регулярных
выражений, определяющих этот язык [1, 3].
Предлагаемый алгоритм может быть полезен в некоторых
приложениях, например, в лексическом и синтаксическом анализе и т.д. Также
рассматриваемая задача тесно связана с проблемой звёздной высоты,
которая является одной из важных проблем в теории формальных языков [3]. Опубликованные на сегодняшний день алгоритмы
решения данной проблемы [6, 7] неприменимы на практике, так как требуют
большого объёма вычислений. Таким
образом, решение поставленной задачи имеет как теоретическое, так и
практическое значение.
Алгоритм точного решения задачи основан
на полном переборе. Применяется метод последовательной элиминации вершин
автомата [8]. Для поиска точного решения необходимо перебрать все n! перестановок вершин
автомата (где n – количество вершин автомата), найти для каждой из
них регулярное выражение и выбрать оптимальное. Но даже для автоматов с
небольшим количеством состояний решение не всегда возможно за приемлемое время.
Эвристические методы
Рассмотрим эвристики для поиска приближённого
решения. С помощью эвристик пытаемся упорядочить состояния автомата таким
образом, чтобы получить регулярное выражение со звёздной высотой, близкой к
минимальной. Будем упорядочивать состояния
автомата следующими способами:
1. В порядке возрастания количества
проходящих через них циклов.
2. По суммарной длине всех проходящих через
них циклов.
3. По суммарной длине всех циклов, но каждое
состояние учитывается только один раз.
4. По произведению количества всех проходящих
циклов и их суммарной длины.
Мультиэвристический подход
Каждая из
эвристик даёт хорошие результаты на определённых классах конечных автоматов. Поэтому
необходимы некоторые методы усреднения значений эвристик. Так как данная
ситуация близка к задаче выбора стратегии в недетерминированных играх,
воспользуемся методами из работ [4, 5].
Для каждой вершины
автомата вычисляется динамическая оценка:
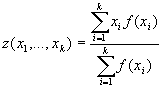 ; где f(xi)
– функция риска.
; где f(xi)
– функция риска.
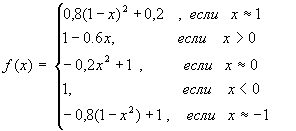
Anytime-алгоритм
Применим незавершённый метод ветвей и границ
[2]. Правую задачу очередного шага будем получать при удалении
следующей вершины. Левую задачу – когда принимаем решение, что данная
вершина не будет удалена на следующем шаге. При получении тривиальной задачи –
запоминаем её решение в качестве текущего псевдо-оптимального
решения. При получении достаточно большой границы исключаем задачу из
последующего решения. Возврат к решению левых подзадач происходит после решения
всех правых подзадач [2]. Вершины для ветвления выбираются в порядке,
определённом с помощью динамических оценок. С помощью anytime-алгоритма
можно получить лучшее решение, найденное за определённый промежуток времени, а последовательность таких решений в
пределе даёт оптимальное решение.
Из
результатов видно, что мультиэвристический подход достаточно
эффективен на задачах небольшой размерности, а решение anytime-алгоритма
даже за короткие промежутки времени даёт хорошее приближение к оптимальному
решению. Кроме того, с помощью anytime-алгоритма можно получить точное
решение значительно быстрее, чем методом полного перебора.
|
Кол-во
вершин автомата |
Среднее
значение звёздной высоты для решений: |
Среднее время точного решения: |
||||||||
|
Точное |
Мульти- эвристи- ческое |
Anytime-алгоритм с ограничением времени: |
Методом полного перебора |
anytime-алгоритма |
||||||
|
1с |
3с |
5с |
10с |
30с |
60с |
|||||
|
3 |
1.8 |
1.8 |
1.8 |
1.8 |
1.8 |
1.8 |
1.8 |
1.8 |
0 |
0 |
|
4 |
1.8 |
1.8 |
1.8 |
1.8 |
1.8 |
1.8 |
1.8 |
1.8 |
0 |
0 |
|
5 |
2.3 |
2.4 |
2.3 |
2.3 |
2.3 |
2.3 |
2.3 |
2.3 |
0 |
0 |
|
6 |
2.6 |
3 |
2.6 |
2.6 |
2.6 |
2.6 |
2.6 |
2.6 |
0.1 |
0 |
|
7 |
3.3 |
3.8 |
3.3 |
3.3 |
3.3 |
3.3 |
3.3 |
3.3 |
1.5 |
0.4 |
|
8 |
3.8 |
4.4 |
3.8 |
3.8 |
3.8 |
3.8 |
3.8 |
3.8 |
16.3 |
4.9 |
|
9 |
4.5 |
5.3 |
4.5 |
4.5 |
4.5 |
4.5 |
4.5 |
4.5 |
210 |
45.5 |
|
10 |
5.1 |
5.9 |
5.2 |
5.2 |
5.2 |
5.1 |
5.1 |
5.1 |
- |
- |
|
11 |
- |
7.3 |
6.5 |
6.1 |
6 |
6 |
5.9 |
5.8 |
- |
- |
|
12 |
- |
8.1 |
7.3 |
7.1 |
6.9 |
6.8 |
6.6 |
6.6 |
- |
- |
Литература:
1.
А. Саломаа. Жемчужины
теории формальных языков. – М.: Мир,
1986. – 159 с.: ил.
2.
Мельников Б.Ф.
Мультиэвристический подход к задачам дискретной оптимизации // Кибернетика и системный
анализ (НАН Украины), 2006, №3. С. 32–42.
3.
Мельников Б.Ф. Недетерминированные
конечные автоматы. – Тольятти, 2001.
4.
Мельников Б.Ф. Эвристики
в программировании недетерминированных игр // Известия РАН. Программирование,
2001, №5. С. 63–80.
5.
Б.Мельников, Н.Романов.
Ещё раз об эвристиках для задачи коммивояжёра. - В кн.: Теоретические проблемы
информатики и ее приложений, вып.4, Саратов, изд-во СГУ, 2001, с.81-92.
6.
K.Hashiguchi: Algorithms for determining relative star height and star
height. – Inform. Comput., 78 (1988) 124-169.
7.
D.Kirsten. Distance desert
automata and the star height problem. – Theoret. Informatics Appl., 39 (2005)
455–509.
8.
B.Melnikov, A.Vakhitova. Some more on the finite automata. – The Korean
Journal of Computional and Applied Mathematics, Vol.5, №3 (1998) 495–506.