Математическое моделирование

Любимова А.А., Нурматов Ш. Р., д.т.н. Потапов В. И.

Южно-Уральский государственный университет филиал в г. Златоусте

Математическое моделирование теплофизических процессов в реакторе на солнечном обогреве для получения карбида кремния

В данной работе рассматривается задача получения карбидокремниевых материалов из растительного сырья, которое следует утилизировать, используя при этом энергию Солнца. Если создать технологические способы переработки отходов рисового производства (рисовой шелухи – РШ), то можно наладить их комплексную переработку для получения ряда ценных материалов, в частности, карбида кремния.

Известно, что обжиг РШ при определенных условиях приводит к образованию карбида кремния, т.к. она на 95% состоит из . В свою очередь огнеупорность карбидокремниевых материалов составляет (185010) .

Карбид кремния (карборунд), благодаря высокой твердости, теплопроводности и тугоплавкости широко применяется в современных отраслях народного хозяйства: инструментальная и химическая промышленность, черная и цветная металлургия, энергетика и т.д.

Так как карборунд в природе не встречается, его получают только искусственным путем – высокотемпературной обработкой. Процесс его получения по стандартным технологиям является очень энергоемким, и к тому же длительным.

С другой стороны, проведение вычислительных экспериментов с математической моделью, реализованной в виде компьютерной программы, обеспечивает сокращение сроков исследования и уменьшение его стоимости. Это позволяет прогнозировать поведение изучаемого объекта в различных, в том числе и экстремальных условиях.

Для проведения эксперимента заготавливаются образцы в виде брикета диаметром 10-15 см из смеси оксида кремния, графита и РШ, которые загружаются в тигль и помещаются в печь.

Для сглаживания неравномерного распределения температуры и карбида кремния по объему, тигль установлен на вращающийся стенд в фокальной зоне БСП, схема которого изображена на рис. 1, 2.

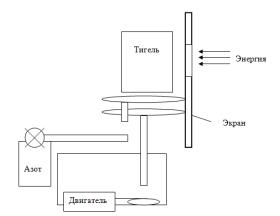
Рис. 1. Схема размещения тиглей на Рис. 2. Схема реактора.

вращающемся столике в фокусе БСП.

Уравнения, описывающие температурные поля внутри реактора и его стенки имеют вид [1,2].

В системе уравнений (1) изменением по температуры стенки и РШ, в виду большой угловой скорости вращения реактора, как показали исследования в работе [3], можно пренебречь.

;

.

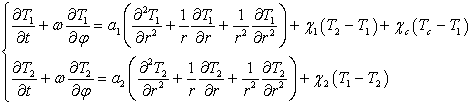(1)

Тогда уравнения примут вид:

(2)

Начальные условия: где (3)

Граничные условия:

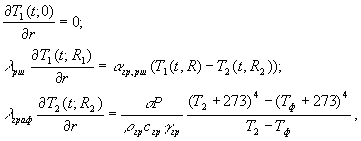(4)

В уравнениях (1) – (4) приняты следующие обозначения:

- постоянная Больцмана, Р – периметр реактора , Р=2, м; - удельная плотность графита, =2100 – удельная теплоемкость графита, =840 - удельный вес графита, =2,2 - температура графитовой стенки, - температура РШ, - температура окружающей среды, - температура фокального пятна, =4000 - шаг по радиусу, м; - коэффициент температуропроводности графита; - коэффициент температуропроводности РШ; – теплопроводность графита, =800 – теплопроводность РШ, =26 , где S – сечение стенки, - коэффициент теплоотдачи. =37 ; =7056 ; ; ; =0.

Преобразуем уравнения (2) в дискретный вид и выразим и . Получим:

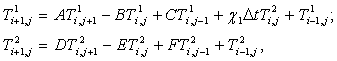(5)

где

А=; В=;

С=; D=;

E=; F=.

Преобразуем начальные условия (3) и граничные условия (4) в дискретный вид:

(6)

где N, M – количество заданных узлов.

Систему (5) и условия (6) представим в матричном виде:

, (7)

где

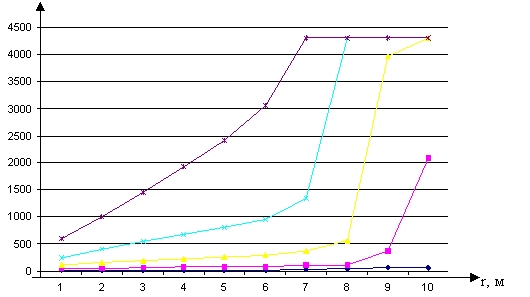
Систему алгебраических уравнений (7) решаем итерационным методом и получаем значения температуры в узлах сетки (рис. 3).

Рис. 3. Распределение температуры внутри реактора и стенки,

- при t = 0,2 c; - при t = 0,4 c; - при t = 0,6c; - при t = 0,8 c; - при t = 1 c.

По результатам математического моделирования можно сделать вывод, что температура по всему радиусу реактора достигнет требуемой для образования карборунда (а именно более 1800 ) достаточно быстро – за 2-4 секунды. Далее необходимо продолжать поддерживать достигнутую температуру 30-45 минут, чтобы прошла реакция карбюризации.

Затраты на изучение процессов получения огнеупорных материалов, закупку необходимого оборудования, строительство установок, а так же требуемые затраты энергии достаточно высоки. Но предварительные оценки показывают, что стоимость продуктов, которые могут быть получены из 1 тонны отходов рисового производства, превышают цену 1 тонны риса-зерна в несколько раз.

Литература:

1. Потапов В. И. Математические модели теплофизических процессов в объектах многослойных структур: Монография. - Челябинск: Изд. ЮУрГУ, 2004. – 270 с.

2. Арутюнов В.А., Бухмиров В.В., Крупенников С.А. Математическое моделирование тепловой работы промышленных печей. - М.: Металлургия, 1990. - 239 с.

3. Любимова А. А. Математическое моделирование теплофизических процессов получения карбида кремния в реакторе на солнечном обогреве /Любимова А. А., Нурматов Ш. Р., Потапов В. И. //Современные инструментальные системы, информационные технологии и инновации. Материалы VII международной научно-технической конференции. Курск: 2011. – С. 188-192.