к.т.н.
Дубчак В.М., ас. Хрипко Т.Є.
Вінницький національний аграрний університет
Активізація індивідуальних здібностей
учнів
на уроках математики.
Актуальною
проблемою сучасної педагогіки є задача відбору
учнів з індивідуальними здібностями та забезпечення їх розвитку. Першою
ланкою до виконання даного завдання стоїть шкільна освіта. Найкраще виділяються
індивідуальні здібності учнів на уроках
математики, адже, шкільний курс математики має забезпечити міцне і свідоме
оволодіння системою математичних знань, умінь, які потрібні для загального
розвитку дитини, їх практичної
діяльності в умовах сучасного виробництва, для вивчення на достатньо високому
рівні споріднених шкільних предметів (фізики, креслення, хімії та ін.) і для
продовження освіти.
Школа повинна готувати освідчених людей з
широким кругозором, які знали б основи науки, розбиралися в основних галузях
виробництва, володіли комп’ютерною технікою, логічним мисленням та методами наукового пізнання.
«Математика розум до порядку приводить» -
ці слова належать великому М.В.Ломоносову. Це дійсно так. Адже однією з
найбільш важливих характеристик мислення є його логічність, можливість робити
правильні висновки, аналізуючи наявні факти. Про людину, у якої добре розвинене
логічне мислення, говорять, що вона ґрунтовно мислить, чітко розмежовує
поняття, оперує конкретними фактами.
Ця найцінніша риса виникає та розвивається
головним чином при вивченні математики, зокрема, в процесі розв’язування задач. Оскільки математика - це практична логіка, в ній кожне нове положення
отримується за допомогою строго обумовлених суджень на основі раніше відомих
положень, тобто строго доводиться. М. В. Ломоносов
наведеними вище словами підкреслив цю особливість математики. Вивчення даного предмета формує не тільки логічне мислення, а й багато інших
рис людини: здогадливість, критичність, акуратність у роботі, цілеспрямованість та ін.
Для загальної
освіти дуже важливо ознайомити учнів з науковими методами дослідження, такими,
як аналіз, синтез, індукція, дедукція, аналогія, тощо. І не лише ознайомити, а й озброїти учнів цими
методами, щоб вони могли практично в конкретних ситуаціях
аналізувати різні твердження, явища, проблеми, виділяти з них важливіші,
систематизувати та класифікувати їх. Вивчення математики у цьому відношенні може дати дуже багато. Взагалі, математика і
властивий їй стиль мислення – істотні елементи загальної культури сучасної
людини.
Ознайомити учнів з цими елементами
культури, дати їм мінімум математичних знань, які потрібно кожній людині, - це
завдання покладене на вчителів та викладачів математики.
Одне з найважливіших завдань шкільної математики – розвивати математичне
мислення учнів.
Спостерігаючи
школярів, учитель не без підстави вважає, що одні учні більш здібні до
навчання, інші менш здібні. Буває так, що учень здібний до математики, але
погано виражає свої думки в усній і письмовій мові чи виявляє здібності до мов,
до літератури, взагалі до гуманітарних наук, але йому важко даються математика,
фізика, вивчення технічних дисциплін.
Здібностями
називаються такі психічні якості, завдяки яким людина порівняно легко здобуває
знання, уміння і навички й успішно займається якою-небудь діяльністю [1].
Здібності не зводяться до знань, умінь і
навичок, хоча виявляються і розвиваються на їх основі. Тому треба бути дуже
обережними і тактовними у визначенні здібностей учнів, щоб не прийняти слабке
знання учня за відсутність у неї здібностей. Подібні помилки
іноді відбувалися навіть у відношенні майбутніх великих учених, що з якихось
причин погано вчилися в школі. По цій же причині
неправомірні висновки про здібності тільки на підставі деяких властивостей, що
доводять не низькі здібності, а недоліки знань[2],
[3].
Підручник
психології К.К. Платонова дає наступне визначення поняттю
"здібність": Здібності — це сукупність таких властивостей
особистості, які визначають успішність навчання якої-небудь діяльності й
удосконалювання в ній. А.В. Петровський у своєму підручнику по загальній
психології дав таке визначення "здібності": Здібності — це такі
психологічні особливості людини, від яких залежить успішність набуття знань,
умінь, навичок, але які самі до наявності цих знань, навичок і умінь не
зводяться [4].
У психології розрізняють загальні та спеціальні
здібності. Під загальними здібностями ми розуміємо таку систему
індивідуально-вольових якостей особистості, яка спроможна забезпечувати
відносно легко продуктивність в
оволодінні знаннями і здісненням різних видів діяльності. Вважається, що
загальні здібності – це явище природного обдарування та всебічного розвитку особистості.
Значна частина спеціалістів вважає, що проблема індивідуальних відмінностей є
однією з самих складних та цікавих. Адже психічні якості людей формуються у житті,
процесі навчання, виховання, діяльності. При однакових умовах,
навчальних програмах, методах навчання ми відмічаємо у всіх індивідуальні
відмінності. Саме тому і цікаві люди, адже всі вони різні. І центральним
моментом в індивідуальних відмінностях є саме здібності кожної людини, адже
саме вони визначають становлення особистості, обумовлюють ступінь яскравості
індивідуальності. Можна сказати, що здібності – це внутрішні умови розвитку
людини, які формуються у процесі її взаємодії із зовнішнім світом.
Під спеціальними здібностями ми розуміємо
систему якостей особистості, яка допомагає досягнути високих результатів у
якійсь спеціальній галузі діяльності. Наприклад, музичній, художній,
літературній та ін. До спеціальних здібностей відносять здібності практичної
діяльності – конструктивно-технічні, організаторські, педагогічні та ін. Тобто,
кожна діяльність висуває визначені вимоги як до загальних так і до спеціальних
здібностей.
Вивчаючи
індивідуальні здібності учнів на уроках математики, вчитель повинний з'ясувати:
по-перше, наскільки в учня розвиті такі риси характеру, як працьовитість, організованість,
зосередженість, наполегливість, витримка, самокритичність, самоконтроль, якщо
виступають як необхідні умови для досягнення стійких успіхів у математичній
науці; по-друге, які математичні інтереси і схильності учня; по-третє,
наскільки в учня розвинуті необхідні для даної дисципліни спеціальні
елементарні здібності, які необхідно розвивати для їх розвитку або для розвитку
якостей особистості, що компенсують деякі з цих здібностей [5].
Як правило, коли кажуть про розвиток
мислення в процесі навчання математики, то мають на увазі розвиток
математичного мислення. Звичайно, це вірно: у процесі навчання математики слід,
у першу чергу, турбуватися не взагалі про розвиток мислення, а саме про
розвиток математичного мислення.
Результати
досліджень багатьох вітчизняних та зарубіжних психологів та дидактів показали,
що математичне мислення є не лише одним з найважливіших компонентів процесу
пізнавальної діяльності учнів, але й таким компонентом, без цілеспрямованого
розвитку якого неможливо досягти ефективних результатів у оволодінні учнями та
студентами системою математичних знань, умінь і навичок.
Розвивати математичне мислення можна за
допомогою спеціально підібраної системи задач, вправ і методики роботи з ними.
Розвиваючій
функції задач в останні роки приділяється особлива увага. Не випадково Д. Пойа,
Е. Резерфорд, А. Ейнштейн та інші зазначали, що задачі не тільки й не стільки
мають сприяти закріпленню знань, тренуванню в їх застосуванні, скільки
формувати дослідницький стиль розумової діяльності, метод підходу до явищ, що
вивчаються[6].
Розвиваюча
функція задач спрямована на розвиток мислення школярів, на формування в них
розумових дій та прийомів розумової діяльності, просторових уявлень, уяви,
алгоритмічного мислення, вміння моделювати ситуацію тощо.
Наведемо приклад однієї із таких
задач та способи її розв’язування.
Постановка
задачі.
Визначити кут між бісектрисами двох плоских кутів правильного тетраедра, які
виходять з однієї вершини.
Розв’зок.![]()
І спосіб:
За означенням правильного
тетраедра [7], яку б грань ми не розглянули,
маємо рівносторонній трикутник.
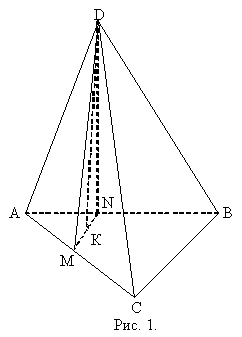 Опустимо з вершини D
тетраєдра DABC бісектриси DM та DN на грані ADC та ADB. (рис.1) Отримаємо
Опустимо з вершини D
тетраєдра DABC бісектриси DM та DN на грані ADC та ADB. (рис.1) Отримаємо ![]() - кут між бісектрисами двох плоских кутів.
- кут між бісектрисами двох плоских кутів.
Нехай ![]() , тоді
, тоді ![]() (середня лінія
трикутника АВС),
(середня лінія
трикутника АВС), ![]() (за властивістю
бісектрис рівносторонніх трикутників
АDC, ADB) та
(за властивістю
бісектрис рівносторонніх трикутників
АDC, ADB) та ![]() .
.
З ![]() - рівнобедреного, де
- рівнобедреного, де ![]() - висота трикутника та
- висота трикутника та ![]() і
і ![]() , за означенням
, за означенням ![]() ;
; ![]() .
.
Тоді, ![]() , де
, де ![]()
(Також слід зауважити, що
![]() можна знайти за
теоремами косинусів та синусів:
можна знайти за
теоремами косинусів та синусів:
За теоремою синусів: ![]() де
де ![]() ,
, ![]() ,
, ![]() .
.
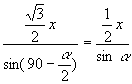 ,
,
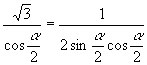 ,
,
![]()
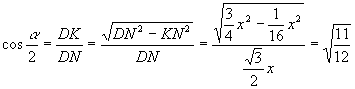 ,
,
![]() , де
, де ![]()
За теоремою косинусів: ![]()
![]() ,
,
![]() , де
, де ![]() )
)
ІІ спосіб:
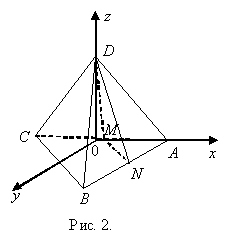 Розмістимо правильний
тетраєдер DABC у декартовій системі координат, причому так, щоб вершина D
лежала на додатній піввісі і проектувалася в центр основи ΔАВС,
розміщеного в пл. XОY, тобто в т.(0;0;0). (рис.2)
Розмістимо правильний
тетраєдер DABC у декартовій системі координат, причому так, щоб вершина D
лежала на додатній піввісі і проектувалася в центр основи ΔАВС,
розміщеного в пл. XОY, тобто в т.(0;0;0). (рис.2)
Нехай т.А(1;0;0), тоді
т.В(x1;y1;0) та т.С(x2;y2;0).
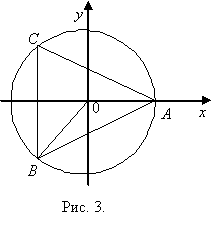
Опишемо навколо ΔАВС
одиничне коло та знайдемо координати точок В і С з означення тригонометричних
функцій (мал.3):
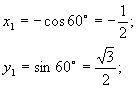 тобто т.В(
тобто т.В(![]() ).
).
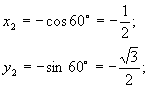 тобто т.С(
тобто т.С(![]() ).
).![]()
За формулою відстані між
двома точками: АВ=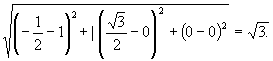
 За розміщенням у просторі
т. D
За розміщенням у просторі
т. D![]() , тоді
, тоді ![]() ,
, ![]() .
.
Так як ![]() , то отримаємо рівність
, то отримаємо рівність ![]()
![]() ; звідси
; звідси ![]() та
та ![]() (не задовольняє умові
розміщення т. D).
(не задовольняє умові
розміщення т. D).
Отже т. D(![]() ).
).
Проведемо з вершини D
бісектриси ![]() і
і ![]() плоских кутів
плоских кутів ![]() і
і ![]() (рис. 2). За
побудовою
(рис. 2). За
побудовою ![]() - середня лінія ΔАВС, тобто т.М
- середня лінія ΔАВС, тобто т.М![]() - середина сторони АВ, т.
- середина сторони АВ, т.![]() - середина сторони АС.
- середина сторони АС.
Знайдемо координати точок
![]() і
і ![]() :
:
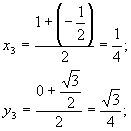 т.
т.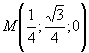 ,
,
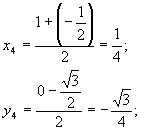 т.
т. 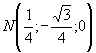 .
.
Тоді, 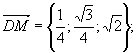
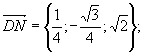
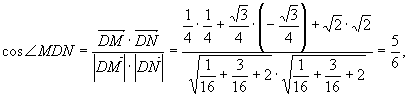 де
де ![]()
ІІІ спосіб:
Розглянемо більш
загальний випадок побудови тетраедра DABC з довільною стороною а та довільними
координатами його вершин.
Нехай т.А![]() . за координатами цієї точки послідовно побудуємо інші три
точки, вказавши їх координати.
. за координатами цієї точки послідовно побудуємо інші три
точки, вказавши їх координати.
 Для спрощення обчислень ,
побудуємо ΔАВС в площині XOY декартової системи координат. Таким чином,
т.А
Для спрощення обчислень ,
побудуємо ΔАВС в площині XOY декартової системи координат. Таким чином,
т.А![]() , т.В
, т.В![]() , т.С
, т.С![]() .
.
Знову ж таки для
спрощення обчислень приведеної моделі, нехай одна із сторін (наприклад АВ),
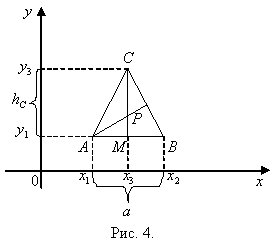
буде паралельна одній із координатних осей (наприклад осі ОХ) (рис.4), тоді 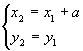 т.В
т.В![]()
Очевидно з рис.4, що
координати т.С ΔАВС будуть слідуючими:
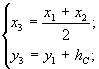
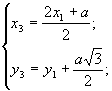 т.С
т.С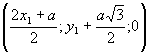 .
.
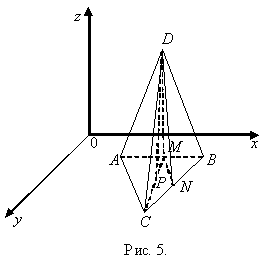 Нехай т. Р – точка
перетину висот ΔАВС, тобто СМ=
Нехай т. Р – точка
перетину висот ΔАВС, тобто СМ=![]() =
=![]() , тоді РМ=
, тоді РМ=![]() =
=![]() . Отже, т.Р
. Отже, т.Р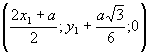 .
.
В свою чергу четверта
вершина D тетраєдра DABC проектується в т. Р ΔАВС (рис.5) і матиме
слідуючі координати: т. D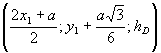 , де
, де ![]() - висота тетраєдра DABC, опущена з вершини D на грань
ΔАВС.
- висота тетраєдра DABC, опущена з вершини D на грань
ΔАВС.
З ΔDPB, маємо: ![]() або
або ![]() , де
, де ![]()
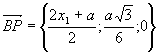 ,
, ![]() .
.
Тоді, ![]()
![]()
Отже, т. D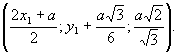
Знайшовши послідовно всі
чотири вершини тетраедра DABC, кожне ребро якого рівне a, знайдемо координати
точок M і N, які відповідають основам апофем DM та DN побудованого тетраедра:
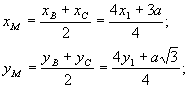 т. М
т. М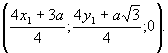
![]()
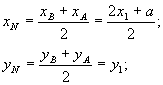 т. N
т. N![]()
Тоді, 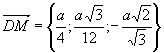 та
та 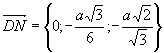 ,
,
![]()
![]() ;
;
![]() (скалярний добуток
векторів)
(скалярний добуток
векторів)
Отже, 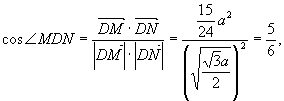 де
де ![]()
Значення тригонометричної
функції шуканого кута ![]() можна знаходити використовуючи і векторний добуток векторів.
Оскільки, для площі ΔDNM тетраедра DABC справедливі такі співвідношення:
можна знаходити використовуючи і векторний добуток векторів.
Оскільки, для площі ΔDNM тетраедра DABC справедливі такі співвідношення:
![]() SΔDNM=
SΔDNM=![]() , де
, де ![]() - векторний добуток
векторів, звідси слідує, що
- векторний добуток
векторів, звідси слідує, що 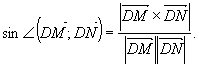
Оскільки, 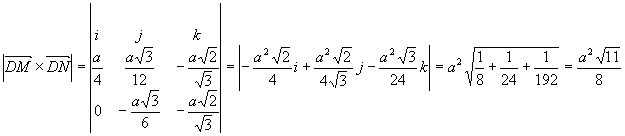 та
та ![]()
![]() , то
, то 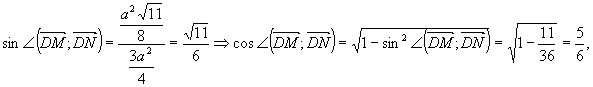
![]()
IV спосіб:
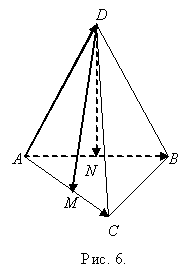 Розглянемо правильний
тетраєдер DABC (рис.6) та введемо такі позначення:
Розглянемо правильний
тетраєдер DABC (рис.6) та введемо такі позначення: ![]() . Відомо, що
. Відомо, що ![]() та
та ![]() .
.
За властивістю векторів: ![]() та
та ![]()
![]()
Тоді, 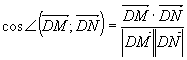 , де
, де
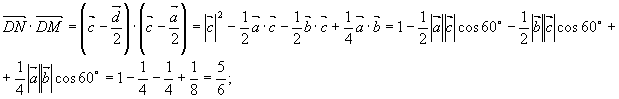
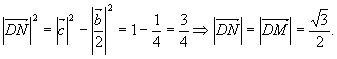
Отже, 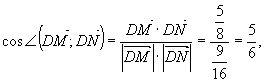 де
де ![]()
Задачі
відіграють визначальну роль у розвитку математичного мислення учнів, оскільки,
розв'язуючи їх, учні привчаються робити правильні висновки, виділяти головне,
порівнювати і протиставляти факти, знаходити загальні ознаки і зв'язки між поняттями,
виділяти відомі вихідні дані і невідомий шуканий результат.
Розв'язування
задач привчає до повноцінної аргументації, завдяки якій не допускаються
необгрунтовані узагальнення й аналогії, вимагається повнота аналізу умови
задачі, прояв аналітико-синтетичної діяльності.
При такому
багатогранному підході у учнів та студентів формується особливий стиль
мислення, що характеризується чіткістю побудови формально-логічної схеми
міркувань і лаконічністю висловлювання думки, індуктивною і дедуктивною логікою
доказів, точністю формулювань. Тому саме задачний підхід рекомендується
застосовувати в методичній системі розвитку індивідуальних здібностей учнів на
математичних уроках та заняттях, що
дозволяє обрати стратегію навчання математично обдарованих дітей, завдяки якому
засвоєння навчального матеріалу відбувалося б адекватно пізнавальним
можливостям учнів. Такий підхід відбиває природу продуктивного мислення людини,
і тому найбільш доцільний з точки зору розвитку індивідуальних здібностей учнів
та студентів. Особливо ефективно це
виявляється в навчанні математики, де задача грає особливу роль, виступаючи і
засобом і методом навчання[8].
Римський імператор Цицерон говорив:
«Інтелект – це здатність людини керуватися розумом, відчуттям і волею». Тому
учитель математики, розвиваючи та активізуючи на своїх
цікавих уроках розумову діяльність учнів, виховує інтелектуально розвинену
особистість.
Розв'язування
математичних задач як специфічний вид навчально-пізнавальної діяльності є
ефективним засобом формування творчої обдарованості учнів. Розроблений варіант
методичної системи роботи викладача з математично
обдарованими учнями та студентами, побудований на
принципі навчання математики через розв'язування задач, продемонстрував
ефективність і доцільність запропонованого підходу. Підпорядкування навчальної
роботи на уроках математики і позакласної роботи єдиній педагогічній ідеї –
задачному підходу до навчання математики, дало у віддачі належний результат, який виявився в розвитку
інтересу учнів до математики та їх здобутках в інтелектуальних математичних
змаганнях.
Література:
1. Голубєва Е.А. Здібності й
індивідуальність. - М.: Прометей, 1993.
2. Здібності і схильності / за редакцією Голубєвої Е.А. - М.:
Педагогіка, 1989.
3. Пізнавальні процеси і здібності в навчанні / за редакцією
Шадрикова В.Д. - М.: Освіта, 1990.
4. Платонов К.К. Проблема здібностей. - М.: Наука, 1972.
5. Колінець Г.Г. Структура дослідницьких здібностей у
школярів // Психологічні аспекти розвитку здібностей та творчої обдарованості в
дошкільному та шкільному віці. – Матеріали міжрегіональної конференції
“Психологічна наука і сучасний заклад народної освіти”. – Частина 4. –
Запоріжжя, 1994. – С. 48-49.
6. Колінець Г.Г. Шкільний психолог і формування
дослідницьких здібностей школярів // Психологічна служба школи: минуле,
сучасність, майбутнє. – Матеріали міжнародної конференції. – Тернопіль, 1996. –
С. 134-135.
7. М.
Я. Вигодський. Довідник з елементарної математики. Київ, 1953. – С. 309-310.
8. Самовол П. І. Методична система
роботи із здібними та обдарованими з математики учнями в середній школі.: Дис.
канд. пед. наук: 13.00.02 /
УДПУ ім. М. П. Драгоманова. . К., 1995. . 221с.