Физика/5. Геофизика
Ларченко И.Н., Закинян Р.Г.
Ставропольский государственный университет, Россия
Описание геострофического ветра во влажной
атмосфере с учетом геоидальной формы Земли
Рассмотрим движение сухого воздуха, описываемого уравнением движения идеальной жидкости с учетом вращения Земли в геоидальной системе координат:
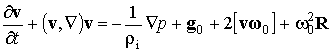 .
(2.1.1)
.
(2.1.1)
Под геоидальной системой координат здесь мы понимаем декартовую систему
координат, в которой ось ![]() направлена
перпендикулярно поверхности Земли, имеющей форму геоида. Следовательно, оси
направлена
перпендикулярно поверхности Земли, имеющей форму геоида. Следовательно, оси ![]() и
и ![]() лежат в
плоскости, касательной к поверхности геоида. Запишем уравнение (2.1.1) в
проекциях на оси координат:
лежат в
плоскости, касательной к поверхности геоида. Запишем уравнение (2.1.1) в
проекциях на оси координат:
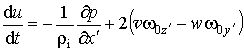 , (2.1.2)
, (2.1.2)
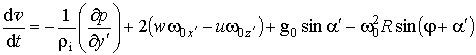 , (2.1.3)
, (2.1.3)
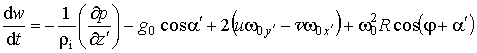 . (2.1.4)
. (2.1.4)
Здесь ![]() – угол между плоскостями касательными к сфере и геоиду.
Угол
– угол между плоскостями касательными к сфере и геоиду.
Угол ![]() находим из
условия формирования геоида, т.е. из равенства проекций на горизонтальную
плоскость центробежной силы инерции, обусловленной вращением Земли, и силы
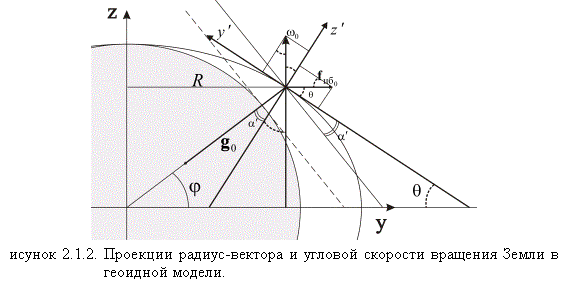
тяготения (рис. 2.1):
находим из
условия формирования геоида, т.е. из равенства проекций на горизонтальную
плоскость центробежной силы инерции, обусловленной вращением Земли, и силы
тяготения (рис. 2.1):
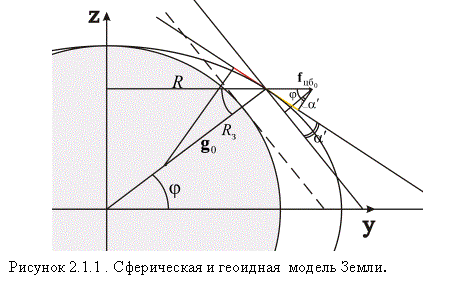
![]() .
.
Осуществив преобразования, получим:
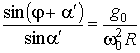 ,
, 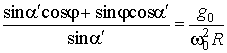 ,
,
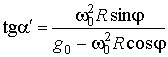 ,
,
так как ![]() и
и ![]() , то
, то
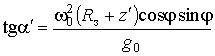 . (2.1.5)
. (2.1.5)
На полюсах и на экваторе касательные плоскости сферической
и геоидной модели параллельны, следовательно ![]() , а значит
, а значит ![]() . На широте
. На широте ![]() :
: ![]() .
.
Проекции угловой скорости вращения Земли с учетом геоидности
![]() ,
,
![]() ,
,
![]() .
.
Используя условие формирования геоида, получим систему уравнений:
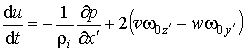 , (2.1.6)
, (2.1.6)
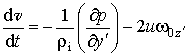 , (2.1.7)
, (2.1.7)
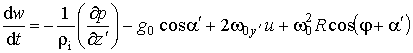 . (2.1.8)
. (2.1.8)
В состоянии равновесия (статики):
![]() ,
, 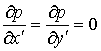 ,
,
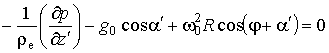 .
(2.1.9)
.
(2.1.9)
Здесь ![]() – плотность воздушной частицы;
– плотность воздушной частицы; ![]() – плотность
окружающей воздушную частицу атмосферы. В стационарном состоянии невозмущенной
атмосферы
– плотность
окружающей воздушную частицу атмосферы. В стационарном состоянии невозмущенной
атмосферы ![]() получим условия
существования геострофического ветра:
получим условия
существования геострофического ветра:
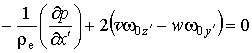 , (2.1.10)
, (2.1.10)
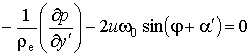 , (2.1.11)
, (2.1.11)
 .
(2.1.12)
.
(2.1.12)
Из уравнения (2.1.11), получим выражение для скорости геострофического
ветра вдоль оси ![]() :
:
 . (2.1.13)
. (2.1.13)
Параметры окружающей атмосферы мы рассматриваем как невозмущенное состояние. Из уравнения состояния влажного воздуха следует
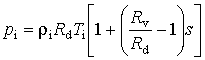 ,
, 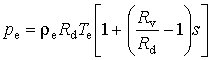 ,
(2.1.14)
,
(2.1.14)
где ![]() ,
, ![]() – давление
внутри и снаружи воздушной частицы;
– давление
внутри и снаружи воздушной частицы; ![]() ,
, ![]() – температура,
соответственно, внутри и снаружи воздушной частицы;
– температура,
соответственно, внутри и снаружи воздушной частицы; ![]() – удельная
газовая постоянная сухого воздуха;
– удельная
газовая постоянная сухого воздуха; ![]() – удельная
газовая постоянная водяного пара;
– удельная
газовая постоянная водяного пара; ![]() – массовая доля водяного пара;
– массовая доля водяного пара; ![]() – универсальная
газовая постоянная;
– универсальная
газовая постоянная; ![]() – молярная
масса сухого воздуха;
– молярная
масса сухого воздуха; ![]() – молярная
масса водяного пара.
– молярная
масса водяного пара.
Далее, учитывая численные значения удельных газовых постоянных сухого
воздуха ![]() и водяного пара
и водяного пара
![]() , а также, что
, а также, что
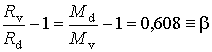 ,
,
уравнения (2.1.14) запишем в виде
![]() ,
, ![]() .
(2.1.15)
.
(2.1.15)
Сделаем
следующее приближение: изменением давления в горизонтальной плоскости в
уравнении состояния воздуха пренебрежем, т.е. допустим, что ![]() . Отсюда следует, что
. Отсюда следует, что
![]() . (2.1.16)
. (2.1.16)
Или
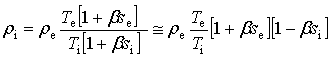 .
.
Учитывая, что ![]() , запишем
, запишем
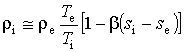 . (2.1.17)
. (2.1.17)
Другими словами, мы допускаем, что плотность зависит от температуры и массовой доли водяного пара и не зависит от давления. То есть мы добавляем к приближению Буссинеска зависимость плотности влажного воздуха от массовой доли водяного пара [21]. Будем считать, что температура окружающей атмосферы изменяется по закону:
![]() , (2.1.18)
, (2.1.18)
где ![]() – градиент
температуры окружающего воздуха;
– градиент
температуры окружающего воздуха; ![]() – температура
окружающего воздуха у земли. То есть влиянием водяного пара на изменение
температуры с высотой пренебрежем. Будем также считать, что подъем влажной
воздушной частицы происходит адиабатически. Тогда температура поднимающейся
влажной воздушной частицы будет изменяться по закону:
– температура
окружающего воздуха у земли. То есть влиянием водяного пара на изменение
температуры с высотой пренебрежем. Будем также считать, что подъем влажной
воздушной частицы происходит адиабатически. Тогда температура поднимающейся
влажной воздушной частицы будет изменяться по закону:
![]() , (2.1.19)
, (2.1.19)
где ![]() – температура
поднимающейся воздушной частицы у земли;
– температура
поднимающейся воздушной частицы у земли; ![]() –
сухоадиабатический градиент температуры. Представим
–
сухоадиабатический градиент температуры. Представим
![]() , (2.1.20)
, (2.1.20)
![]() – функция
перегрева. Тогда формула (2.1.17) запишется в виде
– функция
перегрева. Тогда формула (2.1.17) запишется в виде
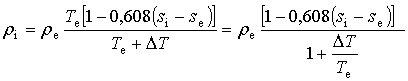 .
(2.1.21)
.
(2.1.21)
В условиях атмосферы можно воспользоваться следующим приближением:
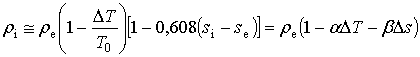 ,
(2.1.22)
,
(2.1.22)
где  ,
, ![]() К;
К; ![]() – функция
пересыщения. Для атмосферы
– функция
пересыщения. Для атмосферы ![]() . С учетом формул (2.1.18) и (2.1.19) функция перегрева
запишется в виде:
. С учетом формул (2.1.18) и (2.1.19) функция перегрева
запишется в виде:
![]() , (2.1.23)
, (2.1.23)
где ![]() – значение
функции перегрева у земли;
– значение
функции перегрева у земли; ![]() .
.
Для адиабатически поднимающейся воздушной частицы массовая доля водяного пара остается постоянной
![]() ,
,
![]() – массовая доля
водяного пара у земли. Пусть в окружающей атмосфере массовая доля водяного пара
убывает по линейному закону
– массовая доля
водяного пара у земли. Пусть в окружающей атмосфере массовая доля водяного пара
убывает по линейному закону
![]() , (2.1.24)
, (2.1.24)
где ![]() – градиент
массовой доли водяного пара в окружающей атмосфере. Тогда для функции пересыщения получим выражение
– градиент
массовой доли водяного пара в окружающей атмосфере. Тогда для функции пересыщения получим выражение
![]() , (2.1.25)
, (2.1.25)
где ![]() – пересыщение у
земли.
– пересыщение у
земли.
С учетом формул (2.1.23) и (2.1.25) формула (2.1.22) для плотности воздушной частицы запишется в виде
![]()
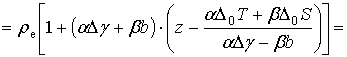
![]() .
.
Отсюда найдем уровень выравнивания плотностей воздуха в воздушной частице и окружающей атмосфере
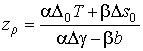 . (2.1.26)
. (2.1.26)
Из формулы (2.1.26) видно, уровень выравнивания плотностей воздуха для влажной частицы выше, чем уровень выравнивания температур поднимающегося сухого воздуха.
Тогда выражение (2.1.12) запишется в виде:
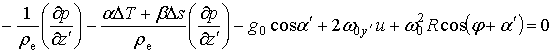 .
.
(2.1.27)
Если предположить, что в стационарном состоянии выполняется уравнение статики атмосферы в виде (2.1.9), то из выражения (2.1.27) следует равенство:
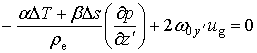 , (2.1.28)
, (2.1.28)
из которого для скорости зонального переноса получим выражение:
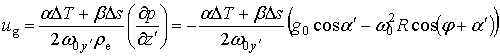 ,
,
или приближенно, в силу малости угла ![]() :
:
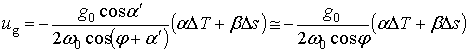 .
(2.1.29)
.
(2.1.29)
Учтем, что
![]()
![]()
тогда
![]()
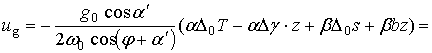
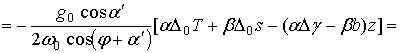
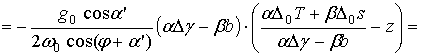
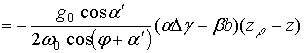 (2.1.30)
(2.1.30)
То есть имеет место широтный перенос воздуха. Оценим это значение
скорости при следующих значениях параметров: ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Подставляя численные значения, для скорости
зонального переноса получим значение
. Подставляя численные значения, для скорости
зонального переноса получим значение ![]() . Если воздух сухой, то получаем
. Если воздух сухой, то получаем ![]() , и, наоборот, если
, и, наоборот, если ![]() , а
, а ![]() получаем
получаем ![]() . Отрицательный знак говорит о том, что движение
воздуха направлено с востока на запад. Из формулы (2.1.30) следует, что
величина скорости зонального переноса зависит от знака разности плотностей воздушной частицы и окружающей
атмосферы, которая меняются с высотой. При
. Отрицательный знак говорит о том, что движение
воздуха направлено с востока на запад. Из формулы (2.1.30) следует, что
величина скорости зонального переноса зависит от знака разности плотностей воздушной частицы и окружающей
атмосферы, которая меняются с высотой. При ![]() ,
, ![]() и
и ![]() – поток
западный, то есть, направлен с запада на восток, при
– поток
западный, то есть, направлен с запада на восток, при ![]() ,
, ![]() и
и ![]() .
.
Эмпирически установлено, что скорость зонального
потока прямо пропорциональна ![]() . В полученном нами выражении (2.1.29) зональная
скорость также увеличивается с увеличением широты, определен коэффициент
пропорциональности, зависящий от функций перегрева и пересыщения.
. В полученном нами выражении (2.1.29) зональная
скорость также увеличивается с увеличением широты, определен коэффициент
пропорциональности, зависящий от функций перегрева и пересыщения.
Приравнивая выражения (2.1.13) и (2.1.29), получим
выражение для градиента давления по оси ![]() , вызванное наличием возмущений температуры и
влажности:
, вызванное наличием возмущений температуры и
влажности:
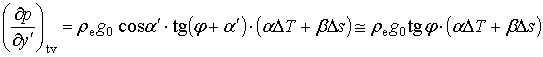 ,
,
т.е. изобарическая поверхность наклонена к плоскости геоида, и этот наклон определяется функциями перегрева и пересыщения воздуха.
Литература
1. Волочай М.А., Грицаева М.Н., Закинян Р.Г.
Свободная конвекция влажного воздуха. //Материалы 55-й научно-методической
конфренции преподавателей и студентов Ставропольского государственного
университета «Университетская наука – региону». Ставрополь: СГУ, 2010, С. 16 – 19.
2. Динамическая
метеорология. Теоретическая метеорология. /Под ред. Д. Л. Лайхтмана. – Л.: Гидрометеоиздат, 1976, 607 с.
3. Матвеев
Л.Т. Физика атмосферы. СПб: Гидрометеоиздат, 2000, 779 с.
4. Матвеев
Л.Т. Курс общей метеорологии. Физика атмосферы. Л.: Гидрометеоиздат, 1984, 752
с.