Д.т.н. Кирсанов Ю.А., к.т.н. Назипов Р.А., Данилов В.А.^*

Исследовательский центр проблем энергетики Казанского научного центра РАН (Академэнерго КазНЦ РАН)

^* Казанский государственный энергетический университет (КГЭУ)

Получение критериальных уравнений внутренней

теплоотдачи и сопротивления высокопористых тел

Предложенные ранее геометрическая модель высокопористого ячеистого материала (ВПЯМ) [1], модель тепловых процессов в пористом цилиндре с нагретой боковой поверхностью и охлаждаемым однофазным теплоносителем [2] и методика исследования теплоотдачи в пористом цилиндре [3] открыли возможность для экспериментального исследования внутренней теплоотдачи и гидродинамического сопротивления образцов ВПЯМ.

Исследования проводились на 11 медных и нихромовых цилиндрических образцах, боковая поверхность которых нагревалась от внешнего нагревателя. В осевом направлении через образец продувался однофазный холодный теплоноситель (воздух), давление которого падало на величину . Образцы ВПЯМ имели следующие характеристики пористости: объемная пористость e_v = 0,8…0,97; диаметр сферических пор d_sph = (0,8…4,59)·10^-3 м; эквивалентный диаметр каналов d_eq = (0,7 …5,27)·10^-3 м; эквивалентный диаметр перемычек каркаса d_sk = (0,012 …0,078)·10^-3 м; удельная поверхность каркаса f_sk = 879…4900 м^-1.

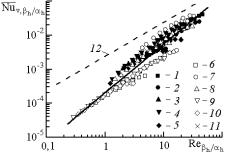
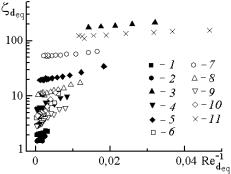
Результаты исследования сопротивления показаны на рис.1,а. Точки, относящиеся к отдельному образцу, обобщены уравнением

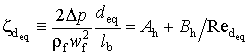, (1)

где - коэффициент сопротивления; - плотность, кг/м³; – скорость фильтрации, м/с; и – коэффициенты регрессии; ; – динамическая вязкость, Па·с.

а) b)

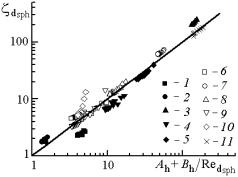
Рис.1. Гидравлические характеристики образцов

1-11 – номера образцов; а) – индивидуальные и b) – обобщенная характеристики

Вязкостный и инерционный коэффициенты модифицированного закона Дарси

, (2)

выражающиеся через коэффициенты регрессии и формулами

, , (3)

были обобщены для всех исследованных образцов критериальными уравнениями:

, (4)

, (5)

где = 5,82·10^-17, = 2,54·10^-13 для и = 6,85·10^-17, = 2,88·10^-13 для ; – диаметр сферической поры, отнесенный к 1 мм.

Все точки, показанные на рис. 1,а, аппроксимированы также уравнением (1), коэффициенты и в котором вычислены по формулам (3)-(5). Результаты показаны на рис. 1,b. Среднеквадратичное отклонение точек от аппроксимирующей линии составляет 30%.

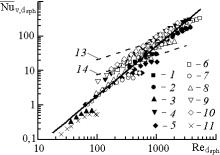
Результаты исследования теплоотдачи образцов ВПЯМ показаны на рис. 2 в координатах (рис. 2,а), (рис. 2,b) и (рис. 2,c), где ; ; ; ; ; - объемный коэффициент теплоотдачи, Вт/(м³К); - поверхностный коэффициент теплоотдачи, Вт/(м²К); - теплопроводность, Дж/(кг·К).

Линии 12 отвечает критериальное уравнение, рекомендуемое для разных пористых структур, кроме ВПЯМ [4]

. (6)

Линии 13 и 14 соответствуют уравнению, рекомендуемому для ВПЯМ [5]

, (7)

при = 0,8 (линия 13) и = 0,97 (линия 14).

а)	b)	c)
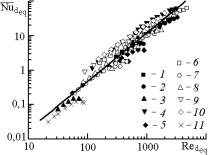
Рис. 2. Теплоотдающие характеристики образцов ВПЯМ 1-11 – номера образцов; 12 –уравнение (6); 13, 14 – уравнение (7)

Из рис. 2,b видно, что полученные результаты находятся в удовлетворительном согласии с данными работы [5]. Средние квадратичные отклонения точек от аппроксимирующего уравнения регрессии колеблются от 47% (рис. 2,a и c) до 49% (рис. 2,b). Отсюда следует, что ни один из рассмотренных определяющих размеров (, и ) не дает каких-либо преимуществ перед другими – во всех случаях наблюдается значительное расхождение опытных значений чисел Нуссельта. Это указывает на необходимость использования при обобщении результатов по внутренней теплоотдаче ВПЯМ дополнительных безразмерных параметров. Большой набор характеристик пористости, получаемый с помощью геометрической модели ВПЯМ [1], дает такую возможность.

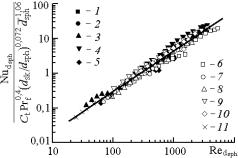
На рис. 3 показано обобщение результатов по внутренней теплоотдаче ВПЯМ в диапазоне 25 ≤ ≤ 5360 критериальным уравнением

, (8)

где в качестве определяющего размера применен как эквивалентный диаметр каналов , так и диаметр пор . Присутствие в уравнении (8) помимо определяющего размера также и диаметра перемычки указывает на то, что механизм внутренней теплоотдачи в ВПЯМ может рассматриваться как совокупность теплоотдачи при течении в каналах диаметром и теплоотдачи при поперечном обтекании перемычек каркаса диаметром . Среднее квадратичное отклонение точек от уравнения (8) не превысило 27%.

Рис. 3. Обобщенная характеристика внутренней теплоотдачи ВПЯМ: 1-11 – номера образцов

Литература

1. Кирсанов Ю.А., Назипов Р.А., Данилов В.А. Геометрические и теплофизические характеристики высокопористой структуры // Изв. вузов. Авиационная техника. 2010. № 2. С. 49.

2. Кирсанов Ю.А., Назипов Р.А., Данилов В.А., Иванова Е.И. Теплопроводность охлаждаемого пористого цилиндра // Известия РАН. Энергетика. 2011. № 4. С. 128-137.

3. Кирсанов Ю.А., Назипов Р.А., Данилов В.А., Башкирцев Г.В. Математическая модель тепловых процессов и методика исследования теплоотдачи в пористом цилиндре // Изв. Самарского научного центра РАН. Т. 12. № 4. С. 90-96.

4. Зейгарник Ю.А., Иванов Ф.П. Обобщение опытных данных по внутреннему теплообмену в пористых структурах // ТВТ. 2010. Т. 48. № 3. С. 402-408.

5. Гортышов Ю.Ф., Муравьев Г.Б., Надыров И.Н. Экспериментальное исследование течения и теплообмена в высокопористых структурах // ИФЖ. 1987. Т. 53. № 3. С. 357-361.