Технические науки/5.Энергетика

К.т.н. Павлюков В.С., инж. Павлюков С.В.

ФГБОУ ВПО «Южно-Уральский государственный университет»(НИУ)

Моделирование режимов электроэнергетической системы с использованием коэффициентов распределения и элементов диакоптики

Развитие математического моделирования режимов современных электрических систем больших размеров является актуальной задачей с реформированием электроэнергетики и становлением рынка электроэнергии и мощностей. На рассматриваемом этапе развития доминирующей моделью исследования режимов данных объектов являются узловые уравнения в форме баланса токов, мощностей в декартовой или полярной системе координат [1], что приводит к проблеме решения задач большой размерности. С развитием рынка в электроэнергетике появляются потребности в усовершенствовании существующих [2] и разработке новых моделей и алгоритмов, на основе которых будут создаваться более современные и эффективные технологии анализа процессов и задач электроэнергетики, в том числе расчета характерных установившихся режимов, энергораспределения [3], прогнозирование электропотребления и других, предусматривающих высокое быстродействие и качество результатов.

В предлагаемой работе решение данных процессов рассматривается с использованием коэффициентов распределения совместно с элементами диакоптики, идея которой заключается в разделении большой системы на сети меньших объемов и разных уровней напряжений, что далее позволит сформировать процесс моделирования управления электрической системой в иерархической структуре при разных комбинациях исходных, физически существующих режимных параметрах.

При разделении схемы замещения большого объема электрической системы на N подсистем (для иллюстрации изложения зададим N=2), то аналитические выражения для векторов-столбцов токов в ветвях дерева при задании режимных параметров в виде векторов-столбцов узловых токов (узловых мощностей) запишутся в виде

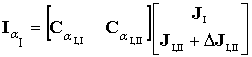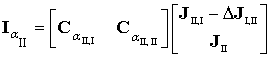, (1) , (2)

где , – векторы-столбцы внутренних задающих токов узлов первой и второй подсистем, соответственно; , – векторы-столбцы задающих узловых токов во множестве граничных узлов подсистем; – вектор-столбец множества задающих граничных токов, перетекающих через граничные узлы из подсистемы I в подсистему II при их объединении; , – подблоки матриц собственных (l = I или II) и взаимных ( k= I,II при kl) коэффициентов распределения деревьев подсистем разделенной схемы электрической системы.

Для обеспечения сохранения режима исходной и разделенной схемы электрической системы необходимо соблюдение на границе между подсистемами следующего условия

, (3)

для которого на основании закона Ома с использованием токов ветвей (1), (2) деревьев подсистем, получаем

(4)

(5)

В формулах (4), (5) компоненты , – подблоки матриц коэффициентов распределения граничных узлов, соответствующих разомкнутым схемам подсистем–деревьям, , – диагональные матрицы полных сопротивлений ветвей деревьев подсистем; , – векторы-столбцы токов ветвей деревьев подсистем(при отсутствии э.д.с. в ветвях), – операция транспонирования.

Совокупность аналитических выражений в матричном виде (3)–(5) моделируют между подсистемами большой разделенной системы структуру связи, которая представляется вектором-столбцом граничных задающих токов

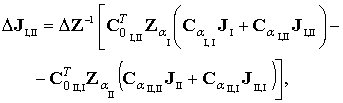(6)

где , – диагональная матрица сопротивлений ветвей дерева (k принимает значения I или II).

Векторы-столбцы напряжений узлов подсистем моделируются выражениями

(7)

, (8)

где – напряжение балансирующего узла между смежными подсистемами; е – единичная диагональная матрица.

Матричные уравнения (1) – (8) представляют математическую модель, алгоритм которой позволяет выполнять расчеты установившихся режимов больших электроэнергетических систем по иерархическому способу. В силу нелинейности модели итерационное решение можно организовать, используя алгоритм одношагового циклического процесса, а также более сложный, но со скоростью в окрестности сходимости решения, которую обеспечивают методы типа Ньютона.

Иллюстрация апробации предлагаемой модели осуществлялась с использованием элементов диакоптики на примере схемы электрической сети, представленной следующими исходными данными, где напряжение (кВ) базисного узла ; вектор полных мощностей (МВА) в узлах схемы корректируется с учетом условий [4]; параметры ветвей(Ом) схемы и соединения их ; начальные приближения(0–верхний индекс) элементов вектора-столбца комплексных узловых напряжений полной схемы замещения электрической сети

= , погрешность вычисления напряжений узлов вектора-столбца принята кВ.

С целью определения работоспособности описанного выше подхода был выполнен расчет установившегося режима для данной электрической системы в среде Visual Studio 2005. Деления полной схемы сети реализовано на две подсхемы с соответствующими множествами узлов. К первой (I) подсхеме отнесена некоторая часть полной схемы с множеством узлов под номерами 1 и 2, ко второй (II) подсхеме – ее часть, с оставшимся множеством узлов, порядковые номера которых 3 и 4. Результат решения был достигнут за одну итерацию, что позволяет данную модель развивать далее для применения к практическим расчетам.

Для сравнения эффективность предложенного выше подхода рассмотрим применение широко известной Z – модели [2]. При этом будет производиться контроль для текущих величин элементов векторов напряжений на итерационном процессе по неравенству

, (9)

где – текущая итерация для вычисления составляющих вектора узловых напряжений .

Выполненные исследования вычислений на ЭВМ узловых напряжений представлены в таблице.

Таблица – Текущие значения напряжений узлов схемы разделенной на две подсхемы

Номер t-й итерации
1	110,038–j2,781	107,428–j2,524	108,983–j0,945
2	109,743–j2,97	106,737–j3,058	108,526–j0,741
3	109,603–j2,938	106,421–j2,949	108,367–j0,845
4	109,563–j2,976	106,321–j3,028	108,301–j0,816
5	109,543–j2,971	106,275–j3,012	108,278–j0,831
6	109,537–j2,977	106,261–j3,023	108,269–j0,827

Используя достаточно простой алгоритм одношагового циклического процесса, результат с заданной точностью при разделении системы на две подсистемы достигается за шесть итераций.

С целью сопоставления работоспособности описанного выше подхода был выполнен расчет установившегося режима для той же электрической системы в среде Visual Studio 2005. Результат решения был достигнут за одну итерацию, что позволяет данную модель развивать далее для применения к практическим расчетам. Использование элементов диакоптики для задачи расчетов потерь мощности(энергии) в больших системах снимет традиционный вопрос, связанный с большой размерностью задачи, что её позволит решать на более качественном уровне.

Интеграция данного подхода, сочетающая аппарат диакоптики и коэффициентов распределения, с элементами искусственных нейронных сетей[4], способствуют развитию параллельной обработки вычислений раздельных подсистем, гарантирующих решение задач при разных вариантах исходных, физически существующих, режимных параметрах.

Литература

1. Лыкин, А.В. Электрические системы и сети[Текст]: учебное пособие по направлению «Электроэнергетика» / А.В. Лыкин. – М.: Логос, 2008. – 253 с.

2. Тарасов, В.И. Теоретические основы анализа установившихся режимов электроэнергетических систем / В.И. Тарасов – Новосибирск: Наука, 2002. – 344 с.

3. Конов, Г.А. Исследования режимов распределения потоков энергии в электрических сетях/ Г.А. Конов, А.В. Паздерин, Е.А. Плесняев //Вестник УГТУ–УПИ. – 2000. – №2(10). – С. 55–60.

4. Павлюков, В.С. Модели прогноза потерь энергии на базе достоверизации схемно-режимных параметров электрических сетей / В.С. Павлюков, С.В Павлюков // Электрика. – 2009. – №12. – С. 14-20.