Куликовский К.Л., Гареев Ш.И.
Самарский государственный технический университет, Россия
Математическая модель траектории
движения для управляющей системы планирующего зонда
На сегодняшний
день разработаны различные робототехнические средства для проведения
исследовательских работ в морях и океанах. Важное место среди вышеуказанных
средств занимает класс планирующих зондов (ПЗ). Перемещение таких средств
основано на действии гидродинамических сил на зонд при изменениях центра
тяжести и плавучести последнего. На данный момент математические модели
различных форм движения ПЗ отсутствуют, в частности не изучена одна из важных
форм движений ПЗ - движение по спирали. Данное движение требуется при
мониторинге, расположенных в морях и океанах нефтяных и газовых платформ, по
всему периметру от поверхности до дна водного пространства. Модель подобного
движения ПЗ, позволит спрогнозировать траекторию перемещения по периметру
контролируемого объекта, выполняя требуемые манёвры.
Управление маневрированием ПЗ заключается
в изменении крена, дифферента и плавучести, путём изменения массы зонда, и
перемещении центра тяжести ПЗ, путём смещения груза относительно условной
системы координат корпуса вдоль и вокруг собственной оси (рис. 1,а,б).
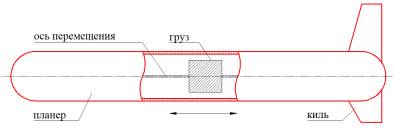
а)
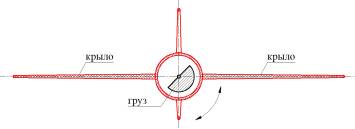
б)
Рис.
1. Перемещение груза вдоль (а) и вокруг (б) оси ПЗ
За счёт смещения центра тяжести ПЗ
изменяет крен и дифферент. Масса зонда изменяется при помощи выкачивания
(всплытие) и закачивания (погружение) жидкости во внутренний резервуар.
Увеличивая массу (уменьшая плавучесть) и дифферент на нос, ПЗ погружается, а
при обратном процессе зонд всплывает, если при этом создать крен на одну из
сторон, ПЗ начнёт маневрировать в сторону крена.
Рассмотрим более детально силы,
действующие на зонд при погружении по спирали (рис. 2,а,б). В первом
приближении пренебрегаем моментами инерции и демпфирования, так как
рассматривается равномерное движение без переходных процессов в статическом
режиме.
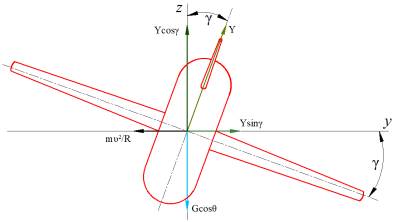
a)
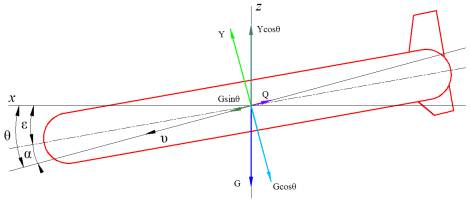
б)
Рис. 2. Вид ПЗ
спереди (а) и сбоку (б) при движении по спирали
На рис. 2: Y–подъемная сила, Q–сила лобового сопротивлении, υ–вектор скорости, G–результирующая выталкивающей силы и силы тяжести, mυ2/R–центробежная
сила, γ–угол крена, α–угол атаки, ε-угол наклона, θ–угол
дифферента.
Изучив силы, действующие на ПЗ, можно
найти следующие необходимые для определения траектории движения параметры: угол
атаки, радиус спирали и скорость.
Значение
угла атаки ПЗ определяется соотношением:
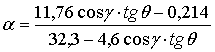 (1)
(1)
Радиус спирали определяется выражением:
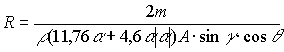 (2)
(2)
Скорость движения ПЗ определяется выражением:
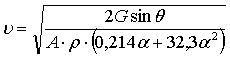 (3)
(3)
Исходя,
из полученных соотношений координаты ПЗ в различные моменты времени
определяются системой уравнений.
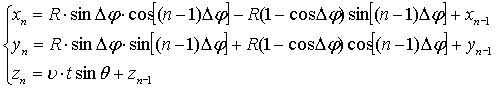 (4)
(4)
На основании (4) построим графики траектории движения ПЗ по спирали в горизонтальной (рис.3)
и в вертикальной плоскости (рис.4).
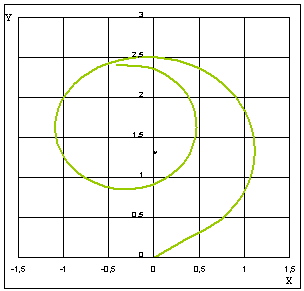
Рис. 3. Траектория
движения ПЗ в горизонтальной плоскости
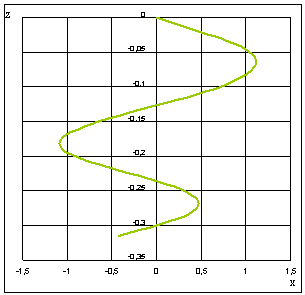
Рис. 4. Траектория
движения ПЗ в вертикальной плоскости
Как
видно, из приведенных рисунков ПЗ погружается против часовой стрелки и совершив
пол витка спирали увеличивает крен, тем самым уменьшая радиус траектории
движения.
Таким
образом, соотношения (4) являются математической моделью, которая позволяет
спрогнозировать траекторию движения ПЗ при любых изменениях радиуса,
скорости, крена, дифферента и угла атаки, и выбрать наиболее рациональную
траекторию движения, необходимую для исследования заданного объекта. Так же
полученные результаты являются основой для определения траектории движения ПЗ в
динамическом режиме.
Литература:
1. Joshua G. Gaver, Ralf Bachmayer, Naomi Enrich
Leonard. Underwater Glider Model Parameter Identification. Published by the
author, Proc. 13th Int. Symp. on Unmanned Untethered Submersible Technology
(UUST), August 2003.