Ìàòåìàòèêà/5. Ìàòåìàòè÷íå ìîäåëþâàííÿ

Romanyshyn Y.M.^1),2), Pukish S.R.¹⁾, Kokhalevych Y.R.¹⁾

¹⁾ Lviv Polytechnic National University

²⁾ University of Warmia and Mazury in Olsztyn

USING VOLTERRA SERIES FOR SIMPLIFICATION

THE HODGKIN-HUXLEY NEURON MODEL

Introduction. The Hodgkin-Huxley neuron model [1] is a system of four ordinary nonlinear differential equations of the first order in Cauchy’s form and therefore the mathematical analysis of bioneural structures with large number of neurons using these equations is quite a difficult task. This system of equations contains three internal variables, an exception of which makes it possible to express the output signal through the input one. Such transformation is possible being based on Volterra series, kernels of which are the generalization of linear impulse characteristics to nonlinear systems. Selection a number of components of Volterra series allows taking into account the nonlinear properties of different orders. Features of Volterra series construction for some models of neurons, including the Hodgkin-Huxley model, are considered in [2-4]. However, despite the possibility of such representation of Hodgkin-Huxley model of neuron, this method of neuron modeling is studied insufficiently, that specifies the relevance of the paper.

The purpose of this paper is to analyze features of the representation of Hodgkin-Huxley model of neuron by Volterra series, calculation of kernels of the series, possibilities of simplification of the model based on this representation and calculation of the first order kernel in the spectral and time form.

Formulation of the problem of representation of Hodgkin-Huxley neuron model in the form of Volterra series. The system of equations of Hodgkin-Huxley neuron model we represent as [1, 2]:

; ;

; , (1)

where ; - density of the external current of the neuron activation; - specific surface capacitance of the membrane; ; - time; - voltage on the neuron membrane; , , - internal functions of time and membrane voltage, which determine the time dependence of current densities and nonlinear properties of conductivity and are related with by the formulas:

;

; ;

; ; ;

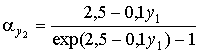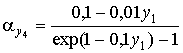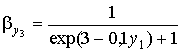; ; , (2)

where , , - reference voltage sources for ions , and other ions respectively; , , - constant components of ion channels conductivity; the value is set in mV and the values and in msec^-1.

The values of parameters of classic Hodgkin-Huxley model [1] are: ; ; ; ; ; ; .

The representation of the signals through input signal in the form of the following Volterra series is searched as:

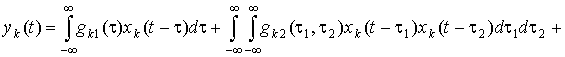
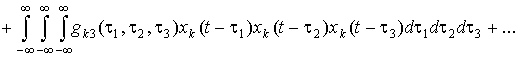, (3)

where ; ; - kernels of Volterra series for the -th variable of appropriate order.

Calculation of kernels of Volterra series. It is more convenient to carry out calculation of Volterra kernels in the frequency domain [2]. Let carry out the Fourier transform of Volterra series:

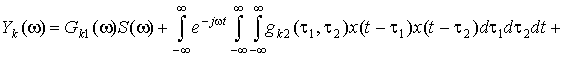
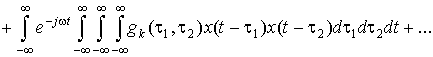, (4)

where - spectra of functions ; - spectra of kernels ; - spectrum of function .

By changing the sequence of integration, using the formula for the multiplication of two signals and spectrum of the signal, displaced in time, this transformation is reduced to the following form:

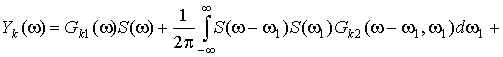
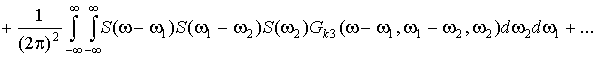. (5)

For decompositions into multiple McLoren series we modify Hodgkin-Huxley model so that the value of functions , and were equal to 0 in equilibrium point of the system (for the function this condition is already provided by the appropriate choice of reference voltage values). For this purpose we calculate the values , and in equilibrium point and modify the system of Hodgkin-Huxley equations by corresponding displacements of these quantities.

After substitution of decompositions in the system of equations (1) we get:

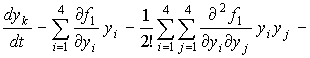
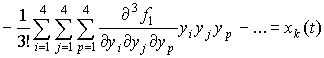. (6)

For obtaining the expressions of derivatives and calculation of their numerical values Symbolic Math Toolbox of MATLAB was used.

After Fourier transform of the system of equations (6) we get:

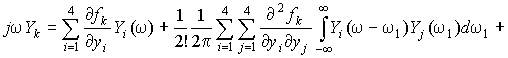
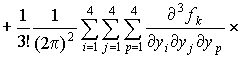
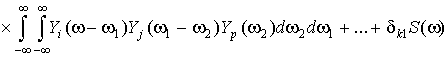, (7)

where - the Kronecker symbol.

After substitution of the expression (5) in the expression (7) we get:

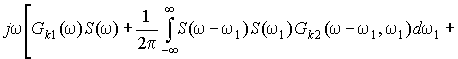
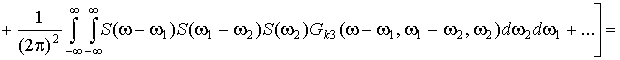
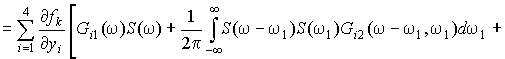
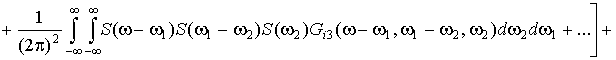
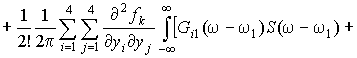
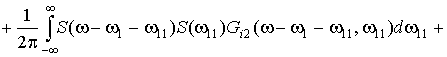
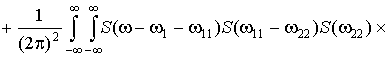
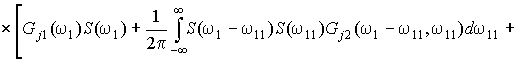
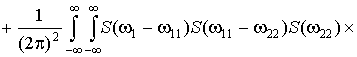
. (8)

Since this equation should be true for any function the equations for calculation of kernels spectra can be obtained by equating the corresponding expressions in (8).

From equating the coefficients at we get:

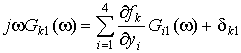; . (9)

This is the system of four linear equations with four unknown first-order kernels. The procedure for its solution is realized in a symbolic form using Symbolic Math Toolbox of MATLAB. As a result, the values are represented by fractional rational expressions with regard to , denominators of expressions are a quarter degree polynomial, numerator of - the third degree polynomial and the numerators of , and – second degree polynomials. 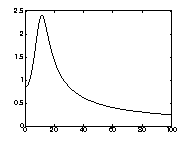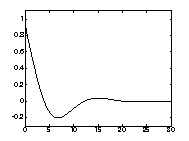Module (spectrum of the first order kernel ) is shown in Fig. 1, a).

The inverse Fourier transform of spectrum is also carried out in the symbolic form with the previous calculation of roots of polynomial denominators. Fig. 1, b) represents a diagram of the first order kernel calculated on the basis of the obtained expressions.

kOhm cm^2

cm^2/F msec^-1

, msec

a) b)

Fig. 1. Module of the spectrum and the first order kernel of Volterra series

The diagrams in Fig. 1 for the module of the first order kernel spectrum and the kernel itself are close to the frequency and impulse characteristics of energy model of neuron, obtained in [5].

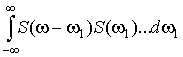From equating the coefficients at in the integrals and further transformations we obtain:

;

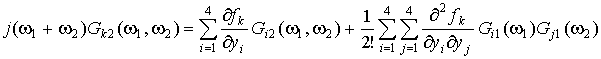. (10)

Similarly to the previous, for the spectra of the second order kernels we obtain the system of linear algebraic equations of the first order with a matrix of the same structure as for the first order kernels.

From equating the double integrals and validity of this equation at arbitrary function we obtain the equation:

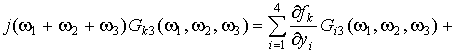
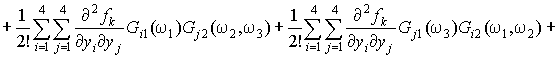
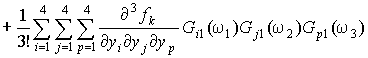. (11)

As in the previous cases of the first and second order kernels, it is a system of four linear algebraic equations with four unknowns and the free terms are expressed by the first and second order kernels.

Similarly, although with much more complicate transformations, we can get the systems of algebraic equations for Volterra kernels of higher orders.

Conclusions. Classical Hodgkin-Huxley neuron model is represented by the system of four nonlinear first order differential equations, which connect input signal (current density), output signal (voltage on the membrane), three internal variables and model parameters. For elimination of the internal variables the reduction of the model to representation as a Volterra series kernels of which are the generalization of impulse response of the linear system for nonlinear systems can be used. Using this model, despite the complexity of the Volterra series, allows us to consider different approximations of neuron model - linear, nonlinear models of different orders. Calculation of Volterra kernels spectra is reduced to solving single-type systems of four linear algebraic equations with four unknowns.

References:

1. Gerstner W., Kistler W.M. Spiking Neuron Models. Single Neurons, Populations, Plasticity. - Cambridge University Press, 2002. - 5,26 MB. - http://diwww.epfl.ch/~gerstner/SPNM/SPNM.html.

2. Kistler W., Gerstner W., Leo van Hemmen J. Reduction of the Hodgkin-Huxley Equations to a Single-Variable Threshold Model // Neural Computation 9(5). – 1015-1045. – 10.1.1.27.3235.pdf.

3. Poggio T., Torre V. A Volterra Representation for Some Neuron Models // Biol. Cybernetics. – 1977. – No. 27. - P. 113-124.

4. Friston K.J. Volterra kernels and effective connectivity / University College London, UK. – 2001. – 26 p. - http://www.fil.ion.ucl.ac.uk/spm/doc/books/hbf2/pdfs/ Ch21.pdf.

5. Smerdov A.A., Romanyshyn Y.M. Electric model of neuron at single excitation // Problems of cybernetics: Biomedinformatics and its applications. – Moscow.: Academy of Sciences of the USSR. – 1988. – P. 168-174 [in Russian].