Математика / 5. Математическое моделирование

Kakzhanov M.U

Using mathematical methods

in reliability theory

Reliability theory [1] - the science of how to ensure the conservation and reliability in the design, manufacture and operation of systems. A necessary condition for the simulation of the Elements of reliability theory is the use of mathematical methods.

Quantitative indicators of reliability of elements and systems include:

- reliability coefficient R_г ;

- the probability of failure-free operation for a specified time P(t); ;

- mean time to first failure Т_m for non-repairable systems;

- MTBF for t_ср recoverable systems:

- the failure rate λ(t);

- mean time to repair τ_m;

- recovery rate μ(t);

- reliability function R_г (t).

Definitions of these values:

R_г - the probability of detecting the product in an efficient condition.

P(t) - the probability that in a given period of time (t) the system does not fail.

Т_m - mean time to the first system failure.

t _m - mean operating time between successive failures of the system.

λ(t) - the expected number of failures per unit time; for easy flow of failures:

λ(t)= 1/ t_m.

τ_m- the expectation of recovery time.

μ(t) - the expected number of rebounds per unit time:

μ(t) = 1/ τ_m

R_г (t) - the change in the system reliability over time.

Systems for the purposes of calculating reliability are grouped into several following criteria using the mathematical apparatus of queuing systems (QS)

- with periodic maintenance - system in which measures to ensure reliability are realized only during scheduled maintenance work at preset intervals that Т_о ;

- with a random period of service - systems in which the measures to ensure the reliability implemented at random intervals;

Depending on the mode of "a compound" of elements in the flowchart distinguished: a. serial (basic compound); b. parallel (redundant connection); in a. combined (in the flowchart holds primary and redundant connection elements); see. Fig. 1.

а.

1

2

…..

n

б.	1
	2
	…..
	n

			3
1				4	…	n
			3
	2	….
1				4	…	n
			3

1. The structures of systems for the purpose of calculating reliability.

Redundant system structures referred to are those in which the failure occurs when the failure of all or a certain number of elements that make up the system.

Redundant structures may be shared with redundant elements of redundant groups and element-wise redundant (see. Fig. 2, a., B., C.).

а.	1	2	3	4
	1	2	3	4

б.	1	2	3	4
	1	2	3	4

в.	1	2	3	4
	1	2	3	4

Figure 2. Options for backup systems.

As shown by the experimental data carried out in various fields of technology, the flow of failures and recoveries is the simplest [2], has ordinary, stationary and lack of aftereffect.

Reliability of complex systems is subject, as a rule, exponential, which is characterized by dependency:

- the probability of failure-free operation:

- distribution function uptime:

- density distribution uptime:

These dependencies correspond to simple flow failures and are characterized by constants:

- The failure rate λ(t) = const; Recovery rate μ (t) = const; MTBF tm = 1 / λ (t) = const; Time to repair τsr = 1 / μ (t) = const.

The parameters λ (t), tm; μ (t) and τsr - prepared by treatment of a number of variations on the work chronometer observation elements and systems.

Reliability coefficient element is determined according to the statistical treatment of variation series by the formulas:

           or (1)

as well as in terms of intensity and failure recovery λ (t) and μ (t):

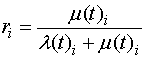(2)

Reliability characteristics of elements in the technical and technological relations are the coefficients of technical r_тi and technological r_ci reliability elements. Reliability element is determined by the following relationship:

r_гi = r_тi ·r_ci . (3)

Reliability of the main systems (series-connected cells) is determined by the presence of only technical failures dependence:

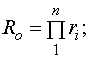     (4)

when reliability elements:

  (5)

where n - the number of series-connected elements in the system;

In the calculations of quantitative indicators and composite structures redundant systems is necessary to know not only their reliability, but also unreliable elements; because the reliability r_i and unreliability q_i element determines the sum of probabilities, forming a complete group, equal to one, then:

 qi = (1 - ri). (6)

The unreliability of the redundant system (for parallel connection of elements) is defined as the probability that all elements of the system failed :

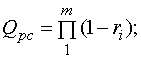                           (7)

Accordingly, reliability, determine the dependence:

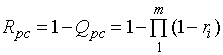             (8)

Or, if reliability elements

 (9)

where m - number of redundant elements.

The degree (m + 1) for calculating the reliability of the system because the system is one element is required, and the number of backup can vary from 1 to m.

Reliability of redundant systems combined with the overall redundancy (system redundancy) defined by the relationship:

(10)

at reliability elements (hence, subsystems):

(11)

Reliability combined systems with redundant groups of elements determined sequentially; first determined the reliability of redundant subsystems, then - the reliability of series-connected subsystems.

Reliability combined systems with element-wise (separate) redundancy is determined sequentially; first determined the reliability block elements (element redundant one, two, and so on up to m elements), then - the reliability of series-connected block elements.

Reliability block element is:

(12)

Reliability combined with R_кj system is element-wise reservation:

(13)

Or, if reliability elements

(14)

The Literature:

1. Methods of technical decisions: Trans. with nem.- Mushik E., P. Muller, M .: Mir, 1990. - 208 S.

2. The reliability and effectiveness of the technique: A Guide In 10 v. V. 5 Design analysis reporting / Ed. VI Patrushev and AI Rembeza. M. Machinery, 1988.- 224 pp