Педагогічні науки / 2. Проблеми підготовки фахівців

Рикова Л.Л.

Комунальний заклад «Харківська гуманітарно-педагогічна академія» Харківської обласної ради, Україна

Використання моделей-аналогів як дидактична умова в процесі підготовки майбутніх вчителів природничо-математичних спеціальностей

Питання про підвищення якості підготовки вчителів (особливо природничих і математичних дисциплін) дуже гостро стоїть в Україні в останнє десятиріччя. З цієї причини за цей час з’явилася велика кількість досліджень, присвячених проблемі поліпшення якості підготовки педагогічних кадрів (Н.П. Емець, М.В. Золочевська, Н.В. Кузьміна, І.П. Подласий, С.О. Семеріков, В.А. Сластенін), і зокрема вчителів природничих і математичних спеціальностей (С.А. Хазіна, Т.П. Куряченко Я.Б. Сікора, А.А. Садикова). Усі дослідники наголошують на необхідності модернізації системи психолого-педагогічної, методичної, практичної підготовки учителів природничо-математичних дисциплін. Одним із шляхів модернізації методичної підготовки майбутніх вчителів є дидактично обґрунтоване використання навчальних моделей у викладанні природничих і математичних дисциплін у процесі педагогічної освіти. Питанням використання моделей у викладанні природничих і математичних наук присвячені роботи І. Богданової, Л. Вішнікіної, І. Левіної, А. Медведєвої, Н. Розової, Л. Фрідмана, Л. Шилової та інших. Проаналізувавши ці дослідження, ми зробили висновок про те, що саме підбір моделей є основною складовою методики викладання природничих і математичних дисциплін.

Розкриття дидактичного потенціалу навчальних моделей повною мірою можливе тільки за умов науково обґрунтованої опори на основні механізми мислення, серед яких в теорії моделювання особливе місце належить аналогії, яка є найважливішим методом пізнання і одним з методів моделювання. В різних розділах природознавства і математики є аналоги як за структурою, так і за видами математичних описів. Усім відома, наприклад, «планетарна модель атома», створена англійським фізиком Ернестом Резерфордом, який для відображення структури атома використав структуру сонячної системи. Більш глибокий приклад: маса (m), момент інерції (I), коефіцієнт жорсткості (k), електрична ємність (C), магнітна індуктивність (L) тощо є кількісними мірами однієї властивості матерії – інертності, тобто будь-яка з цих величин може бути моделлю для всіх інших. Аналіз цих аналогів призводить до розкриття найбільш загальних закономірностей у природі. Розуміння цих закономірностей по суті й представляє собою світорозуміння. Аналогові моделі дають змогу у дослідженні об’єктів деякої предметної галузі використовувати моделі із зовсім інших, спираючись на схожість математичного опису властивостей цих об’єктів або якісь інші аналогії. Особливого сенсу це набуває, якщо за допомогою моделей-аналогів знання з більш дослідженої предметної галузі використовуються для аналізу (вивчення) менш дослідженої. Наприклад, для кращого розуміння коливань електричного і магнітного полів зручно використовувати їх аналог у механіці – механічні коливання, які можна спостерігати безпосередньо. В математичному аналізі аналогом операції інтегрування є операція сумування, оскільки властивості цих операцій ті ж самі (властивість лінійності, адитивності, асоціативності). Аналогія названих властивостей добре ілюструється наступними співвідношеннями:

;

;

;

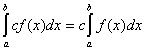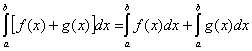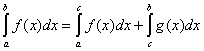Суперпозиція уявлень з різних галузей знань сприяє цілісному сприйняттю кожного об’єкта дослідження, яке ґрунтується на існуванні найбільш загальних закономірностей. Слід відзначити, що погляди на певну науку «очима» інших наук виявляють схожу структуру і схоже змістове наповнення усіх природничих наук – кожна структурна одиниця в природничій науці має аналоги в інших природничих науках. Проілюструємо це математичними формулами для обчислення енергії в різних розділах фізики: формула для обчислення кінетичної енергії поступального руху (1), кінетичної енергії обертального руху (2), енергії пружної деформації твердого тіла (3), енергії електричного поля зарядженого конденсатора (4), енергії магнітного поля соленоїда (5).

(1), (2), (3), (4), (5).

Схожість цих формул, яка є очевидною, не являється випадковою. Їх аналогічність свідчить про те, що наведені формули є відображенням однієї і тієї ж кількісної залежності – енергії різних видів руху матерії від величин, що характеризують опірність усіх видів руху матерії своїй зміні.

Таким чином, у навчально-пізнавальній діяльності застосування методу аналогії відкриває нові можливості щодо підвищення ефективності навчання. Ми визначили такі функції моделей-аналогів у навчанні – пояснювальну, ілюстративну, інтерпретуючу, евристичну, системоутворюючу, світоглядну. Сукупність цих функцій моделей-аналогів забезпечує досягнення гнучкості та системності знань майбутніх вчителів, оволодіння ними прийомами евристичного мислення, досягнення спроможності передбачення властивостей об’єктів вивчення, формування розуміння єдності фундаментальних законів природи, досягнення сформованості наукової картини світу. Отже, використання моделей-аналогів є дидактичною умовою при підготовці вчителів природничо-математичних спеціальностей.

Література:

1. Фридман Л.М. Наглядность и моделирование в обучении. — М.: Знание, 1984

2. Шилова Л.И. Моделирование как метод познания и обучения на уроках математики. Проблеми сучасної педагогічної освіти. Сер.: Педагогіка і психологія. – Зб. Статей: Вип. 16 – Ялта: РВВ КГУ, 2007. –Ч.2.