Костерев Н

Костерев Н. В., Вожаков Р. В., Бондаренко В. И.

Национальный технический университет Украины “КПИ” (г. Киев, Украина)

Оценка состава электроприемников в узле нагрузки энергосистемы для определения устойчивости по напряжению

Предложен метод (способ) оценки состава электроприемников в узле нагрузки энергосистемы для определения устойчивости по напряжению

Ключевые слова: устойчивость узла нагрузки, оценка доли асинхронной нагрузки, метод Ягера.

Для оценки оперативной надежности и планирования режимов энергосистем важной задачей является определение коэффициента запаса статической устойчивости по напряжению узлов нагрузки ЭЭС.

Значение коэффициента запаса статической устойчивости по напряжению в узлах нагрузки определяется по формуле [6]:

где – напряжение в узле нагрузки в рассмотренном режиме; – критическое напряжение в этом же узле, которое отвечает границе, ниже которой имеет место нарушение статической устойчивости двигателей.

Значение минимального коэффициента запаса устойчивости по напряжению в нормальном режиме составляет 0,15, а в послеаварийном – 0,1.

Устойчивость узла нагрузки ЭЭС по напряжению в основном определяется поведением асинхронных двигателей, рассредоточенных в распределительной сети. В свою очередь, устойчивость двигательной нагрузки, присоединенной к узлу распределительной сети, зависит от следующих факторов:

- относительной электрической удаленностью узла ЭЭС от шин узла распределительной сети;

- величины суммарной мощности узла нагрузки распределительной сети;

- долевого значения мощности асинхронной нагрузки в суммарной мощности узла распределительной сети.

На критическое напряжение в узле нагрузки в большой степени влияет долевое значение асинхронной нагрузки в узле нагрузки ЭЭС. Данное значение асинхронной нагрузки может составлять от 5% общей нагрузки узла (узел сельскохозяйственной нагрузки) до 55% (промышленный узел нагрузки) [7]. В современных реалиях эксплуатации ЭЭС информация о режимах и составе асинхронной нагрузки практически отсутствует. К сожалению, зачастую в качестве входной информации для оценки устойчивости являются только общие величины и . А доля двигательной нагрузки остаётся неизвестной. Иногда о ней можно сказать только, что её „мало” или „много”. Перевести такую качественную оценку эксперта, на основании его знаний о конкретном узле нагрузки, в количественную величину можно, используя аппарат нечеткой логики. Для решения этой задачи предлагается применение метода Ягера [4]. Цель которого выбрать из пространства входных признаков (кластеров) центр кластера с наибольшим потенциалом.

Для этого исходя из опыта эксплуатации узла нагрузки ЭЭС формируется исходное множество , состоящее из элементов, характеризующих возможные интервалы долевого коэффициента асинхронных двигателей, подключенных к узлу нагрузки – :

L – интервал «малый» –

M – интервал «средний» –

B - интервал «большой» –

т. е.

Задача состоит в том, чтобы построить нечеткое множество:

Иными словами, необходимо найти степени принадлежности на основе представлений эксперта, какой может быть коэффициент в зависимости от времени суток, рабочие или выходные дни, погоды, знаний о номинальной мощности установленных АД, режимах работы предприятий и т.д.

Предлагаемый алгоритм на основе метода Ягера:

1. Определить объем выборки М (например М = 25, М = 50, М = 100)

2. Разделить единичный интервал на М частей равной длины, например, если М = 50, то получим {1, 0.98, 0.96 …..0.02}. Обозначим это множество .

3. Выбрать случайным образом без возвращения число из .

4. Попросить эксперта перечислить все элементы из , которые, как он полагает, принадлежат уровневому множеству , соответствующему выбранному значению уровня . Предполагаемая степень принадлежности элемента из нечеткому множеству должно быть не меньше случайного числа ( если , а предполагаемое , то этот элемент войдет в ).Иными словами, в включаются все элементы из , которые имеют предполагаемую степень принадлежности большую, чем .

5. Повторять шаги 3-5, пока не используем все из .

6.Определяется частота появления каждого элемента из .:

где – число появления элемента при одинаковом числовом множестве , – число элементов в каждом .

7. Определение вероятности появления каждого элемента из :

8. Полученные оценки вероятностей упорядочить по возрастающей и подставив их в уравнения ( – число элементов в ):

…

Рассчитать степени принадлежности элементов множеству .

Рассмотрим применение данного подхода на примере.

Активная мощность узла нагрузки .

Задаем множество интервалов

1. Объем выборки .

2. Тогда .

3-5. По результатам оценок экспертов определяем уровневые множества нечеткого подмножнства :

, , , , , , , , ,

6. Частота появления каждого элемента:

;

7. Вероятности появления каждого элемента из Х:

;

8. Вероятности упорядоченные по возрастающей:

, ,

Степени принадлежности:

Таким образом, принимаем, что интервал «средний коэффициент» (b) является наиболее предпочтительным решением.

Определение количественного значения выходной переменной

Для определения количественного значения выходной переменной (коэффициент ) будем считать, что отношение индекса сравнения к сумме максимальных индексов сраснения выходных термов определяет степень доверия полученному выводу.

Если имеется большое число индексов сравнения, то в качестве меры недоверия следует принимать среднеарифметическое от всех индексов недоверия (их число – ):

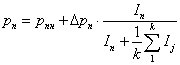
где: – нижняя граница -го выходного терма, который прийнят в кеачестве решения; – интервал -го выходного терма; – сумма максимальних инденксов сравнения выходных термов, .

Для нашей задачи, учитывая что в качестве индекса сравнения применяются степени принадлежности, а выходной переменной является коэффициент (доля асинхронной нагрузки) имеем:

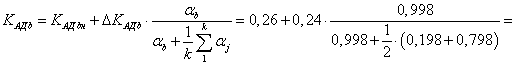
Таким образом, коэффициент для определения активной мощности

асинхронной нагрузки равен 0,42. Следовательно, мощность АД равна:

Тогда статическая нагрузка равна:

Заключение. Предложен приближенный метод оценки мощности эквивалентного асинхронного двигателя в узле нагрузки энергосистемы, основанный на применении нечеткой логики и знаниях эксперта о характеристиках конкретного узла нагрузки ЭЭС, что дает возможность более достоверно определять запас устойчивости по напряжению узла нагрузки ЭЭС в отличие от представления нагрузки известными статическими характеристиками.

Литература

1. Устойчивость нагрузки электрических систем / Ю. Е. Гуревич, Л. Е. Либова, Э. А. Хачатрян.–М.: Энергоатомиздат, 1981.–209 с.

2. Моделирование и динамика атомных электростанций при возмущениях в энергосистеме / Н. В. Костерев.–К.: Вищ.шк., 1986.–168 с.

3. Маркович И. М. Режимы энергетических систем.–М.: Энергия, 1969.–352 с.

4. Ягер Р. Р. Множества уровня для оценки принадлежности нечетких подмножеств. // Нечткие множества и теория возможностей: Сб. научн. тр.–Москва, “Радио и связь”, 1986.–с. 71-78.

5. Режимы работы асинхронных и синхронных электродвигателей / И. А. Сыромятников.–М.: Госэнергоиздат, 1963.–527 с.

6. СОУ-Н МЕВ 40.1.00100227-68: 2012 Стійкість енергосистем: Керівні вказівки.

7. Справочник по проектированию электрических сетей / под ред. Д. Л. Файбисовича. – 4-е изд., перераб. и доп. – М. : ЭНАС, 2012. – 376 с. : ил.