УДК 517.5
ОЦЕНКА СВЕРХУ ПОГРЕШНОСТИ КВАДРАТУРНОЙ
ФОРМУЛЫ НА КЛАССЕ УЛЬЯНОВА – ЧЕБЫШЕВА.
С.С.Кудайбергенов, Д.Х. Исаходжаев.
ЮКГУ им. М. Ауезова, г.
Шымкент.
Пусть даны числа N и s (N,s=1,2,…), b=(b1,…,bN)ÎRN, x=(x(1),…, x(N)), x(n)Î[0,1]s (n=1,2,…,N) и пусть F некоторый класс непрерывных функций s переменных.
Положим
(1)
Здесь интеграл
понимается в смысле Римана, а конечная сумма 
называется
квадратурной формулой (см.[1]).
Пусть для
каждого j (j=1,…,s) задана ортонормированная на R система 
и 
.
Классом
Ульянова – 
называется множество функций 
–
1-периодических по каждой из 
переменных и таких,
что 
:
где 
, 
, 
медленно колебляющиеся
положительные функции при
всех 
), а 
- коэффициент Фурье
функции
по системе 
.
Когда система 
-тригонометрическая,
задача (1) рассмотрена многими авторами и в частности, в 1957 году Н.М. Коробов
(см.[2]) впервые теоретико-числовыми методами для класса 
построил точную в
степенной шкале квадратурную формулу. Затем Н.С.Бахвалов (см.[3]) показал, что 
и 
, а в разных конкретизациях рассмотрены С.А.Смоляком (см.[4]),
Н. Темиргалиевым (см.[5]) и др. (см.[6,7]).
Система
, 
, 
, … , 
(m=2,3,…) называется
системой Чебышева. А коэффициент
Фурье-Чебышева интегрируемой с весом 
функции f(x) определяется по формуле
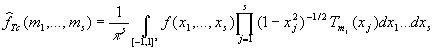(см.[8])
Пусть для
данного целочисленного вектора 
с неотрицательными
компонентами определим множество 
, где 
- целочисленная решетка s-мерного евклидова пространства 
. И при 
рассмотрим квадратурную
формулу
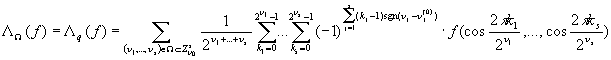
где 
.
Целью
настоящей статьи является оценить сверху погрешность квадратурной формулы 
на классах 
(r>1) и 
.
Справедливы следующие теоремы:
Теорема 1. При r> 1
.
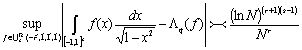Теорема 2. При τ>1
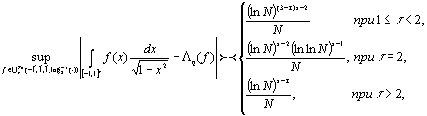
Литература
1. Темиргалиев Н. Теоретико-числовые методы и теоретико-вероятностный подход к задачам Анализа. Теория вложений и приближений, абсолютная сходимость и преобразования рядов Фурье (Продолжение 1) // Вестник Евразийского национального университета. 2002. №3-4.
2. Коробов Н.М. Теоретико-числовые методы в приближенном анализе. М. : Физматгиз, 1963.
3. Бахвалов Н.С. Оценки снизу асимптотических характеристик функций с доминирующей смешанной производной. // Матем. Заметки. 1972. Т.12, №6.
4. Смоляк С.А. Квадратурные и интерполяционные формулы на тензорных произведениях некоторых классов функций // Докл. АН СССР. 1963. т. 148, №5.
5. Темиргалиев Н. Классы Us(β,θ,α;ψ) и квадратурные формулы. // Докл. РАН. 2003. Т.393. №5.
6. Нурсултанов Е.Д., Тлеуханова
Н.Т. О приближенном вычислении интегралов для функций из пространства 
// Успехи матем. наук, 2000. Т.55, №6.
7. Нурсултанов Е.Д., Тлеуханова Н.Т. Квадратурные формулы для классов функций малой гладкости// Матем.сб. 2003. Т.194, №10.
8. Пашковский С. Вычислительные применения многочленов и рядов Чебышева.
М.: Наука, 1983.