УДК 517.443
И. М. Конет, М. П. Ленюк
ВЫЧИСЛЕНИЕ НЕСОБСТВЕННЫХ ИНТЕГРАЛОВ ПО
СОБСТВЕННЫМ ЭЛЕМЕНТАМ ГИБРИДНОГО ДИФФЕРЕНЦИАЛЬНОГО ОПЕРАТОРА БЕССЕЛЯ
-ФУРЬЕ-ЭЙЛЕРА НА ПОЛЯРНОЙ ОСИ
Построим ограниченное на множестве ![]() ={r : r Î(0, R1)
={r : r Î(0, R1)![]() (R1, R2)
(R1, R2)![]() (R2, ¥)} решение сепаратной системы обыкновенных
дифференциальных уравнений Бесселя, Фурье и Эйлера для модифицированных функций
(R2, ¥)} решение сепаратной системы обыкновенных
дифференциальных уравнений Бесселя, Фурье и Эйлера для модифицированных функций
![]() , r Î (0, R1)
, r Î (0, R1)
![]() , r Î (R1, R2) (1)
, r Î (R1, R2) (1)
![]() , r Î (R2,
¥),
, r Î (R2,
¥),
по условиям сопряжения
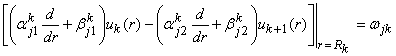 , j, k = 1, 2. (2)
, j, k = 1, 2. (2)
В
системе уравнений (1) принимают участие дифференциальный оператор Бесселя [1] ![]() , дифференциальный оператор Фурье d2/dr2 и дифференциальный оператор Эйлера [2]
, дифференциальный оператор Фурье d2/dr2 и дифференциальный оператор Эйлера [2] ![]() .
.
Предположим,
что выполнены условия на коэффициенты: qj > 0, ![]() ³ 0,
³ 0, ![]() ³ 0, c1kc2k >
0,
³ 0, c1kc2k >
0, ![]() .
.
Фундаментальную
систему решений для дифференциального уравнения Бесселя (![]() )v = 0 образуют модифицированные функции Бесселя
первого рода
)v = 0 образуют модифицированные функции Бесселя
первого рода ![]() (q1r) и второго рода
(q1r) и второго рода ![]() (q1r) [1]; фундаментальную систему решения
для дифференциального уравнения Фурье (d2 / dr2 –
(q1r) [1]; фундаментальную систему решения
для дифференциального уравнения Фурье (d2 / dr2 – ![]() )v = 0 образуют функции v1 = ch q2r и v2 = sh q2r [2]; фундаментальную систему решений для
дифференциального уравнения Эйлера (
)v = 0 образуют функции v1 = ch q2r и v2 = sh q2r [2]; фундаментальную систему решений для
дифференциального уравнения Эйлера (![]() )v = 0 образуют
функции v1 =
)v = 0 образуют
функции v1 = ![]() и v2
=
и v2
= ![]() [2].
[2].
Наличие
фундаментальной системы решений позволяет построить общее решение краевой
задачи (1), (2) методом функций Коши [2, 3]:
u1(r) = A1![]() +
+ 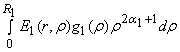 ,
,
u2(r) = A2ch
q2r + B2
sh q2r + 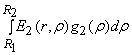 , (3)
, (3)
u3(r) = A3![]() +
+ 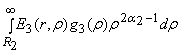 .
.
Здесь Ej(r,
r) – функции Коши [2,
3]:
![]() ,
,
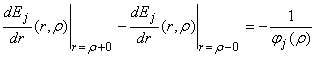 , (4)
, (4)
j1(r) = ![]() , j2(r) = 1, j3(r) =
, j2(r) = 1, j3(r) = ![]() .
.
Определим
функции:
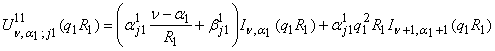 ,
,
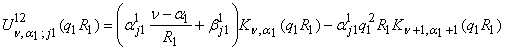 ,
,
![]() .
.
Непосредственно
проверяется, что функция Коши
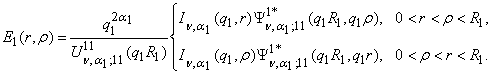 (5)
(5)
Введем в рассмотрение функции:
![]() ,
, ![]() ,
,
![]() ,
,
![]() .
.
Непосредственно
проверяется, что функция Коши
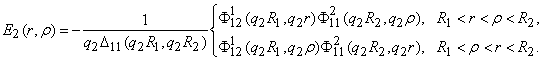 (6)
(6)
Предположим,
что функция Коши
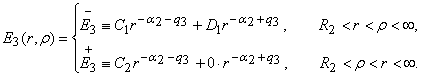
Свойства
(4) функции Коши дают алгебраическую систему из двух уравнений:
![]() ,
,
![]() .
.
Отсюда
получаем соотношения:
![]() ,
, ![]() . (7)
. (7)
Дополним
алгебраическим уравнением:
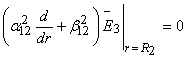 :
: ![]() = 0. (8)
= 0. (8)
Из
алгебраической системы (7), (8) находим, что
C2 = 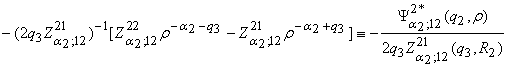 .
.
Этим
функция Коши E3(r, r) определена и в силу симметрии относительно диагонали
r = r имеет структуру:
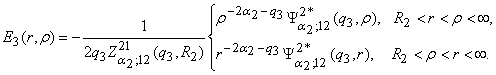 (9)
(9)
Обратимся
к формулам (3). Условия сопряжения (2) для определения величин Aj (j = ![]() ) и B2 дают
алгебраическую систему из четырех уравнений:
) и B2 дают
алгебраическую систему из четырех уравнений:
![]() ,
,
![]() , (10)
, (10)
![]() ,
,
![]() .
.
В алгебраической системе (10) принимают участие функции
G12=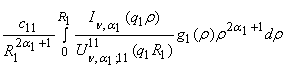 +
+ 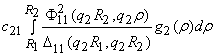 ,
,
G23 = 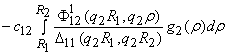 +
+ 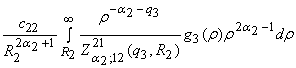 .
.
Введем
в рассмотрение функции:
![]() =
= ![]() , j = 1, 2,
, j = 1, 2,
![]() =
= ![]() ,
,
![]() =
= ![]() ,
,
![]() =
= ![]() .
.
Предположим,
что выполнено условие однозначной разрешимости краевой задачи (1), (2): для
любого ненулевого вектора ![]() = {q1; q2; q3}
определитель алгебраической системы (10) отличен от нуля [4], т.е.
= {q1; q2; q3}
определитель алгебраической системы (10) отличен от нуля [4], т.е.
![]() . (11)
. (11)
Определим
главные решения краевой задачи (1), (2):
1) порожденные неоднородностью условий сопряжения
функции Грина
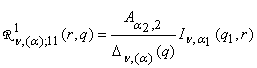 ,
, 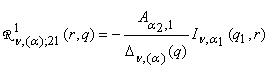 ,
,
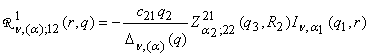 , (a) = (a1, a2, a3),
, (a) = (a1, a2, a3),
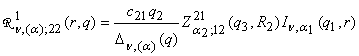 , q = (q1, q2, q3),
, q = (q1, q2, q3),
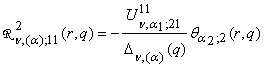 ,
, 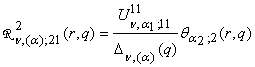 , (12)
, (12)
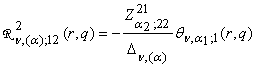 ,
, 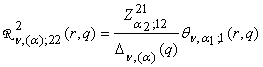 ;
;
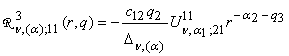 ,
,
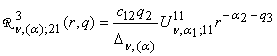 ,
,
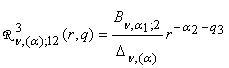 ,
, 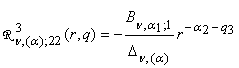 ;
;
2) порожденные неоднородностью системы (1) функции
влияния
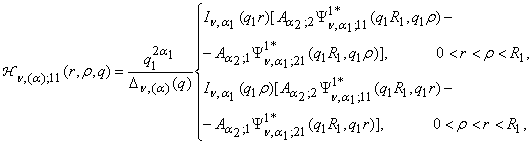
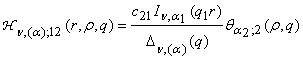 ,
,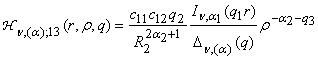 ,
,
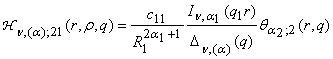 ,
,
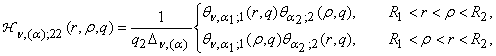 (13)
(13)
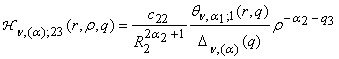 ,
,
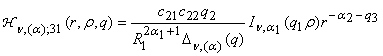 ,
,
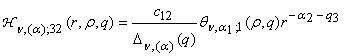 ,
,
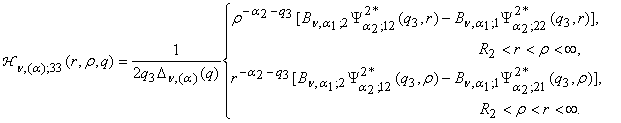
В
результате однозначной разрешимости алгебраической системы (10) в силу условия
(11) и подстановки полученных значений Ai (j = ![]() ) и B2 в
формулы (3) имеем единственное решение краевой задачи (1), (2):
) и B2 в
формулы (3) имеем единственное решение краевой задачи (1), (2):
uj(r) = ![]() +
+ 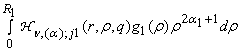 +
+
+ 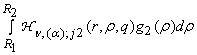 +
+ 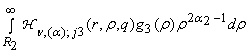 , j =
, j = ![]() . (14)
. (14)
Построим
теперь общее
решение краевой задачи (1), (2) методом
гибридного интегрального преобразования (ГИП), порожденного на множестве ![]() гибридным
дифференциальным оператором (ГДО)
гибридным
дифференциальным оператором (ГДО)
Mn, (a) = q(r)q(R1 – r) ![]() + q(r – R1)q(R2 – r)d2 / dr2+
q(r – R2)
+ q(r – R1)q(R2 – r)d2 / dr2+
q(r – R2)![]() . (15)
. (15)
Поскольку
ГДО Mn, (a)
самосопряженный и имеет одну особую точку r = ¥, то его спектр действительный и непрерывный [5].
Можно считать, что спектральный параметр b Î (0, ¥). Отвечающую ему спектральную вектор-функцию
обозначим через Vn, (a)(r, b) = {Vn, (a); 1 (r, b); Vn, (a); 2(r, b); Vn, (a); 3(r, b)}. При этом функции Vn, (a); j (r, b) должны быть
решением сепаратной системы обыкновенных дифференциальных уравнений Бесселя,
Фурье и Эйлера
![]() , r Î (0, R1)
, r Î (0, R1)
![]() , r Î (R1, R2), (16)
, r Î (R1, R2), (16) ![]() , r Î (R2,
¥)
, r Î (R2,
¥)
по условиям сопряжения
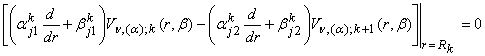 , j, k = 1, 2. (17)
, j, k = 1, 2. (17)
Здесь q(x)–одинична функция Хевисайда [3], bj=(![]() )1/2,
)1/2, ![]() ³ 0, j =
³ 0, j = ![]() .
.
Фундаментальную
систему решений для дифференциального уравнения Бесселя (![]() +
+ ![]() )v = 0 образуют функции
)v = 0 образуют функции ![]() и
и ![]() [1]; фундаментальную
систему решений для дифференциального уравнения Фурье (d2 / dr2 +
[1]; фундаментальную
систему решений для дифференциального уравнения Фурье (d2 / dr2 + ![]() )v = 0 образуют функции v1 = cos b2r и v2 = sin b2r [2]; фундаментальную систему решений для
дифференциального уравнения Эйлера (
)v = 0 образуют функции v1 = cos b2r и v2 = sin b2r [2]; фундаментальную систему решений для
дифференциального уравнения Эйлера (![]() +
+![]() )v = 0 образуют функции v1 =
)v = 0 образуют функции v1 = ![]() cos(b3lnr) и v2 =
cos(b3lnr) и v2 = ![]() sin(b3lnr) [2].
sin(b3lnr) [2].
Предположим,
что
Vn, (a); 1(r, b) = A1![]() (b1r), r Î (0, R1)
(b1r), r Î (0, R1)
Vn, (a); 2(r, b) = A2cos(b2r) + B2sin(b2r), r Î (R1, R2), (18)
Vn, (a); 3(r, b) = A3![]() cos(b3lnr) + B3
cos(b3lnr) + B3![]() sin(b3lnr), r
Î (R2,
¥).
sin(b3lnr), r
Î (R2,
¥).
Условия
сопряжения (17) дают алгебраическую систему из четырех
уравнений
относительно пяти неизвестных:
![]() , j = 1, 2,
, j = 1, 2,
![]() . (19)
. (19)
Решая
алгебраическую систему (19) стандартным способом [4] и подставляя полученные
значения величин Aj (j = ![]() ) и Bk (k = 2, 3) в формулы (18), имеем функции:
) и Bk (k = 2, 3) в формулы (18), имеем функции:
Vn, (a); 1(r, b) = c21 c22b2 b3![]()
![]() ,
,
Vn, (a); 2(r, b) = c22b3![]() [
[![]() –
–
– ![]() ], (20)
], (20)
Vn, (a); 3(r, b) = wn, (a);2(r, b)![]() cos (b3lnr) – wn, (a);1(r, b)
cos (b3lnr) – wn, (a);1(r, b)![]() sin (b3ln
r).
sin (b3ln
r).
В
равенствах (19), (20) принимают участие функции:
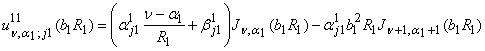 ,
,
![]() ,
,
![]() ,
,
![]() =
= ![]() –
– ![]() ,
,
![]() =
= ![]() +
+ ![]() ,
,
![]() , j = 1, 2;
, j = 1, 2;
![]() , j, k = 1, 2,
, j, k = 1, 2,
![]() , j = 1, 2,
, j = 1, 2,
![]() .
.
Введем
в рассмотрение весовую функцию
s (r) =q(r)q(R1 – r)s1![]() + q(r – R1)q(R2 – r)s2 + q(r – R2)s3
+ q(r – R1)q(R2 – r)s2 + q(r – R2)s3![]() ,
,
где ![]() ,
, ![]() , s3 = 1,
, s3 = 1,
и спектральную плотность
Wn, (a)(b) = b[b3(b)]–1([wn, (a); 1(b)]2 + [wn, (a); 2(b)]2)–1.
Наличие
спектральной функции
Vn, (a)(r, b) = q(r)q(R1 – r) Vn, (a); 1 (r, b) + q(r – R1)q(R2 – r)Vn, (a); 2(r, b) +
+
q(r – R2)Vn, (a); 3(r, b),
весовой функции s(r) и
спектральной плотности Wn, (a)(b) дает возможность определить прямое Hn, (a) и
обратное ![]() ГИП, порожденное на
множестве
ГИП, порожденное на
множестве ![]() ГДО Mn, (a) [5]:
ГДО Mn, (a) [5]:
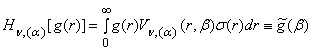 , (21)
, (21)
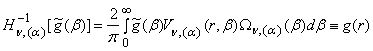 . (22)
. (22)
Здесь
вектор-функция g(r) = {g1(r); g2(r); g3(r)} – любая
функция из области определения ГДО Mn, (a). При
этом
![]() º
º 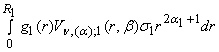 +
+
+ 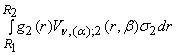 +
+ 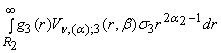 .
.
В
основе применения введенного правилами (21), (22) ГИП для решения
соответствующих задач лежит основное тождество интегрального преобразования ГДО
Mn, (a).
Согласно
с работой [5] имеем утверждение.
Теорема (об основном тождестве). Если вектор-функция f(r) = {![]() [g1(r)];
[g1(r)]; ![]() ;
; ![]() [g3(r)]} непрерывная на множестве
[g3(r)]} непрерывная на множестве ![]() , а функции gj(r) удовлетворяют неоднородным условиям сопряжения (2) и
условиям ограниченности
, а функции gj(r) удовлетворяют неоднородным условиям сопряжения (2) и
условиям ограниченности
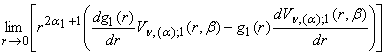 = 0,
= 0,
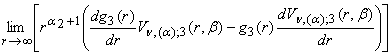 = 0,
= 0,
то имеет
место основное тождество интегрального преобразования ГДО Mn, (a):
Hn, (a)[Mn, (a)[g(r)]] = ![]() –
– ![]() +
+
+
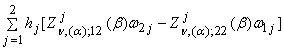 . (23)
. (23)
В
равенстве (23) приняты обозначения:
h1=![]() , h2=
, h2=![]() ,
, 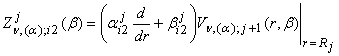 , i,j = 1,2.
, i,j = 1,2.
Единственное
решение краевой задачи (1), (2), построенное по известной логической схеме
методом ГИП, введенного по правилам (21), (22) [5], имеет
структуру:
uj(r) = 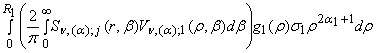 +
+
+
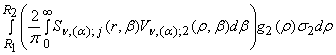 +
+
+
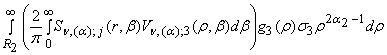 + (24)
+ (24)
+ 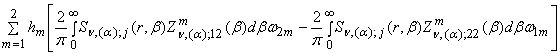 ,j =
,j = ![]() .
.
В
равенствах (24) принимает участие функция
![]() , q2 = max{
, q2 = max{![]() ;
; ![]() ;
; ![]() }.
}.
Сравнивая
решения (14) и (24) в силу единственности, получаем такие формулы вычисления
полипараметрических несобственных интегралов:
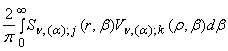 =
= ![]() , j, k =
, j, k = ![]() , (25)
, (25)
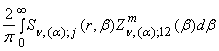 =
= ![]() ,
m = 1, 2, j =
,
m = 1, 2, j = ![]() , (26)
, (26)
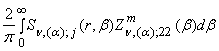 =
= ![]() , m = 1, 2, j =
, m = 1, 2, j =
![]() . (27)
. (27)
Функции
![]() определены по формулам
(13), а функции Грина
определены по формулам
(13), а функции Грина ![]() определены по формулам
(12).
определены по формулам
(12).
Так как
правые части в формулах (25) – (27) не зависят от неравенства (![]() ) ³ 0, то можно положить
) ³ 0, то можно положить ![]() , суживая при этом семью несобственных интегралов.
, суживая при этом семью несобственных интегралов.
Итогом
изложенного выше есть утверждение.
Основная теорема. Если вектор-функция g(r)={g1(r);g2(r);g3(r)}
удовлетворяет условиям теоремы об
основном тождестве и выполняется условие (11) однозначной разрешимости краевой
задачи (1), (2), то имеют место формулы (25)–(27) вычисления
полипараметрических несобственных интегралов по собственным элементам ГДО Mn, (a), определенного равенством (15).
Отметим,
что результаты работы (формулы (25), (26), (27)) пополняют справочную математическую
литературу.
ЛИТЕРАТУРА
1. Ленюк М.П. Исследование основных краевых задач для
диссипативного волнового уравнения Бесселя. – Киев, 1982. – 62 с. – (Препринт /
АН УССР. Ин-т математики; 83.3).
2. Степанов В.В. Курс дифференциальных уравнений. – М.:
Физматгиз, 1959. – 468 с.
3. Шилов Г.Е. Математический анализ. Второй специальный курс. – М.:
Наука, 1965. – 328 с.
4. Курош А.Г. Курс высшей алгебры. – М.: Наука, 1971. –
432 с.
5. Ленюк М.П., Шинкарик М.І.
Гібридні інтегральні перетворення (Фур’є, Бесселя, Лежандра). Частина 1. –
Тернопіль: Економ.
думка, 2004. – 368 с.