Математика / 5. Математичне моделювання

Готинчан І.З.

Чернівецький торговельно - економічний інститут

Київського національного торговельно – економічного університету

МАТЕМАТИЧНЕ МОДЕЛЮВАННЯ ОДНІЄЇ ЗАДАЧІ ДИФУЗІЇ В ШАРОВИХ СЕРЕДОвищах

Постановка проблеми та її аналіз. У класичній теорії теплопровідності на межі області має місце тепловий режим або тепловий потік чи теплообмін через поверхню за законом Ньютона. Якщо межу області (тіла) позначити через , то, не конкретизуючи фізико-технічні характеристики, маємо крайову умову [1,2]:

де точка , - зовнішня нормаль.

Це відображає реально процес поширення теплоти у випадку стаціонарного температурного поля: у цьому випадку можна вважати, що межа тіла є жорсткою по відношенню до відбиття теплових хвиль. Якщо ж температурне поле нестаціонарне, то межа тіла є, взагалі говорячи, м’якою по відношенню до відбиття теплових хвиль. Математично це відображає наявність в крайовій умові диференціального оператора :

Підтвердження цього знаходимо в узагальненій теорії теплопровідності, яка лежить в основі побудови узагальненої термомеханіки [3]. Це особливо стає відчутно, коли ми розглядаємо неоднорідні (кусково-однорідні) середовища. Дана робота присвячена одному із варіантів цієї проблеми.

Основна частина. Розглянемо задачу про побудову обмеженого в області розв’язку сепарат-ної системи диференціальних рівнянь теплопровідності параболічного типу [4]

(1)

за нульовими початковими умовами

(2)

крайовими умовами

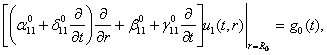
(3)

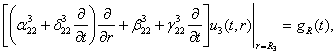(4)

і умовами спряження

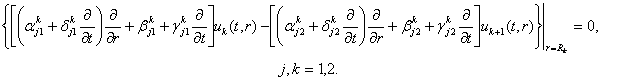(5)

Ми припускаємо, що: 1) та є оригіналами за Лапласом стосовно [5]; 2) виконані умови на коефіцієнти: 3) - диференціальний оператор Лежандра [6]:

,

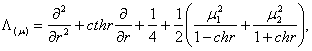
У зображенні за Лапласом параболічній задачі (1)-(5) відповідає крайова задача: побудувати на множині розв’язок сепаратної системи диференціальних рівнянь Фур’є та Лежандра для модифікованих функцій

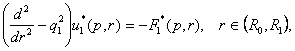
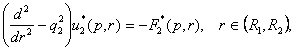(6)

за крайовими умовами

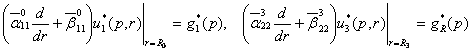(7)

та умовами спряження

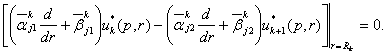(8)

У рівностях (6) – (8) прийняті позначення:

Фундаментальну систему розв’язків для рівняння Фур’є 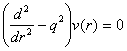утворюють функції та , а фундаментальну систему роз-в’язків для рівняння Лежандра утворюють узагальнені модифіковані приєднані функції Лежандра та [6].

Наявність фундаментальної системи розв’язків дозволяє побудувати розв’язок задачі (6) – (8) методом головних розв’язків [4]:

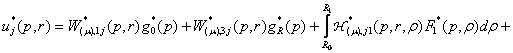
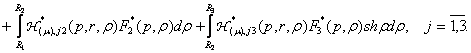(9)

У рівності (9) беруть участь головні розв’язки крайової задачі (6)-(8):

1) породжені крайовою умовою в точці функції Гріна

(10)

2) породжені крайовою умовою в точці функції Гріна

(11)

3) породжені неоднорідністю системи (6) функції впливу

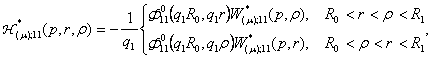
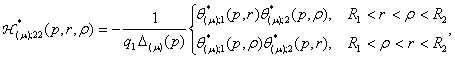
(12)

У рівностях (10)-(12) беруть участь функції:

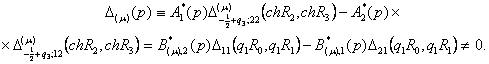
Інші функції і величини загальноприйняті [8].

Повертаючись у формулах (9) до оригіналу, одержуємо єдиний розв’язок параболічної задачі (1) –(5):

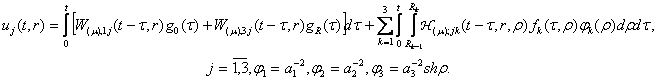(13)

У формулі (13) за означенням [5] функції Гріна

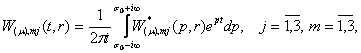(14)

а функції впливу

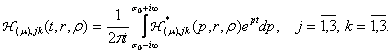(15)

Особливими точками функцій Гріна та функцій впливу є точки галуження і точка . Покладемо Звідси одержуємо, що

У результаті низки елементарних перетворень ми отримуємо трансцен-дентне рівняння корені якого є власними числами гібридного диференціального оператора (ГДО) і утворюють дискретний спектр, а точки є простими полюсами функцій та :

У цій рівності прийняті позначення:

Згідно узагальненої теореми розвинення маємо:

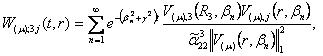
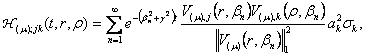
Тут - компоненти власної вектор-функції яка відповідає власному числу :

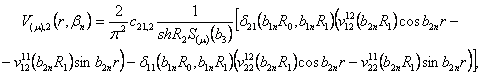
- спеціально введений квадрат норми власної вектор-функціїю

Інші величини загальноприйняті [8,9].

Зауваження. Без залучення нових ідей одержується розв’язок даної задачі, коли початкові умови не нульові та умови спряження неоднорідні.

Висновки. Вектор-функція , де визначені формулою (13) описує в точній аналітичній формі тепловий процес в даному середовищі. Алгоритмічний характер формул (13) дозволяє використовувати одержаний розв’язок як в теоретичних дослідженнях, так і в інженерних розрахунках.

1. Лыков А.В. Теория теплопроводности. – М.: Высшая школа, 1967. – 600 с.

2. Карслоу Г., Егер Д. Теплопроводность твердых тел. - М.: Наука, 1964. -487 с.

3. Подстригач Я.С., Коляно Ю.М. Обобщенная термомеханика. – Киев: Наукова думка, 1976. – 310 с.

4. Тихонов А.Н., Самарский А.А. Уравнения математической физики. – М.: Наука, 1972. 735 с.

5. Лаврентьев М.А., Шабат Б.В. Методы теории функций комплексного переменного. – М.: Наука, 1987. – 688 с.

6. Ленюк М.П.,Шинкарик Н.И. Гибридные интегральные преобразования Лежандра. – Львов, 1989. 60 с. – (Препринт/ АНУССР. Ин-т прикл. проблем механики и математики; 89.0)

7. Степанов В.В. Курс дифференциальных уравнений. – М.: Физматгиз, 1959. – 468 с.

8. Ленюк М.П., Шинкарик М.І. Гібридні інтегральні перетворення (Фур’є, Бесселя, Лежандра). Частина 1. – Тернопіль: Економічна думка, 2004.- 368 с.

9. Ленюк М.П., Петрик М.Р. Інтегральні перетворення Фур’є, Бесселя із спектральним параметром в задачах математичного моделювання масо-переносу в неоднорідних середовищах. – Київ: Наук. думка, 2000.– 371 с.